可重构或可调谐微波滤波器技术

电子可重构，或者说电调微波滤波器由于其在改善现在及未来微波系统容量中不断提高的重要性而正吸引着人们越来越多的关注来对其进行研究和开发。例如，崭露头脚的超宽带（UWB）技术要求使用很宽的无线电频谱。然而，作为资源的频谱是宝贵而有限的，因此，频谱总是被用于多种用途，这意味着当诸如UWB 无线系统这种操作受到关注时，频谱上充满着不期望的信号。在这种情况下，现存的时时处处都在发生变化的不期望的窄带无线电信号有可能会干扰UWB 系统的波段。这种问题的解决方案是在UWB 带通滤波器的通带上引入了一个可进行电切换或电调谐的狭窄的抑制带（陷波）。这种电子可重构滤波器也是宽带雷达或电子军用系统所渴望得到的。我们可以来未雨绸缪地考虑未来的认知无线电和雷达应用，可以肯定的是，可进行电子重构的微波滤波器将会在无线系统中起到一个更重要的作用。

一般来说，为了开发电子可重构滤波器，有源切换元件或调谐元件，如半导体p-i-n 和变容器二极管，射频（RF）微机电系统（MEMS）或其它基于功能性材料的元件，包括铁电体变容器，需要被集成进入无源滤波器结构中。由于微带线滤波器[1]能够便于以很小的尺寸来完成这类集成，因此，人们对于在微带线的基础上开发可调谐或可重构滤波器的兴趣日益增加[2]-[36]。这些滤波器可以分类为可调谐梳状带通滤波器[2]-[9]，射频微机电系统可调谐滤波器[10]-[15]，压电传感器（PET）可调谐滤波器[17]-[19]，可调谐高温超导（HTS）滤波器[21]-[23]，可重构UWB 滤波器[24]-25]，可调谐双频段滤波器[26]，可调谐带阻滤波器[27]-[31]，可重构/可调谐双模滤波器[32]-[36]，以及基于可切换延迟线的可重构带通滤波器。下面，我们将要介绍若干新近开发出来的典型的电子可重构微带线滤波器。

可调谐梳状滤波器

微带线梳状滤波器是开发可调谐或者说可重构带通滤波器颇受欢迎的结构[2]-[9]。图1 是一个3-极点可调谐梳状滤波器的示意图，其中每一个长度小于工作频率的四分之一波长的微带线谐振器的一端是短路相接的，另一端则加载一只变容器。在这个例子中，变容器是基于铁电体钛酸锶钡（BST）薄膜的。每一个BST 变容器的偏置网络包含有一个与变容器相串联的隔直电容器。带通滤波器的中心频率可以通过改变施加到变容器的直流偏置来进行电子调谐。

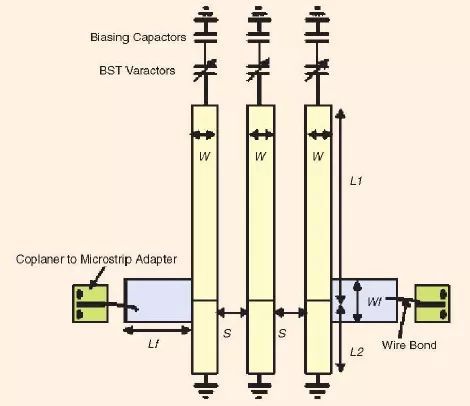
​图1、一个可调谐梳状带通滤波器的示意图[2]。

图2 举例说明了与BST 薄膜进行单片集成的可调谐梳状滤波器的制作和其测量性能。正如在文献[3]中所报道的，对于直流偏置，在BST 薄膜之上，又沉积了一层阻性氮化钽（TaN）薄膜并制作相应的图案。TaN 薄膜的表面电阻率大约是1-10KΩ/每单位面积(Square)，被用来将直流偏置信号导引到电路上，而同时将对电路射频性能的影响减到最小。将BST 薄膜电容器与铝土基片，铜电极，和过孔相集成，从若干个方面推进了可调谐介电技术，这种调谐技术可以开发更复杂的射频和微波电路。

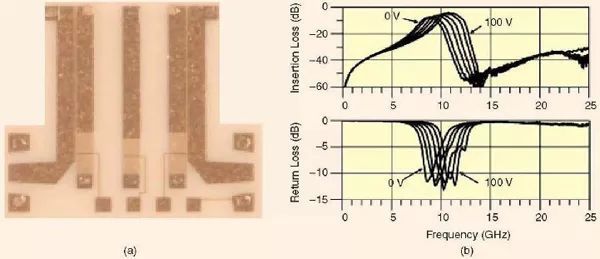
​图2、(a)一个采用了钛酸锶钡薄膜的X-波段（8-12GHz）梳状可调谐滤波器和(b)其测试性能[3]。

在进行中心频率调谐时所出现的带宽波动是一个众所周知的问题。一般来说，为了保持一个与调谐频率无关的绝对的通带带宽，耦合系数必须与调谐频率成反比。已经存在一些解决这个问题的技术，例如文献[4]和[8]。在文献[8]中，人们研究了采用阶梯阻抗微带线谐振器的变容器调谐梳状带通滤波器，这样可以更好地控制谐振器之间的耦合，从而可以通过使用较短电长度的线段元件来满足恒定带宽的要求。同时，人们采用了集总式电感器来作为输入和输出耦合网络，从而使得外部品质因数（Q）直接随着调谐频率而变化。人们已经演示了这种类型的一个四极点滤波器，在2GHz下250MHz 的调谐范围内，3-dB 通带带宽的变化小于3.2%。

在文献[4]中，理论分析表明，对于一个可调谐N-极点滤波器，N 是谐振器的数量，其品质因数（figure of merit） 定义为通带中心频率的偏移与平均通带的比值，它取决于损耗或调谐变容器的Q 值及滤波器的阶数。由于Q 是与功率损耗成反比的，损耗越大，Q 值就越小。一般来说，品质因数（或调谐范围）在小Q 值及大N 值的条件下会有所降低。

人们可以通过实施源/负载多谐振器耦合来设计具有多个传输零点以改善上阻带性能的可调谐平面梳状滤波器。正如在文献[9]中所演示的，这可以通过在经典梳状构造中增加两个新的耦合线而得以实现，如图3（a）所示，其中我们可以看见两条薄的线从源/负载端伸向内部谐振器。图3（b）绘制了所测得的具有分布在上阻带的五个传输零点的滤波器的性能。滤波器的中心频率可以在750MHz 到900MHz 之间进行调谐，滤波器使用的是Philips 公司的BB149 变容二极管，在0V 到20V 的偏置电压下，这个二极管电容值的变化范围是2 到20pF。变容器的偏置元件是6.8pF 和22nH。

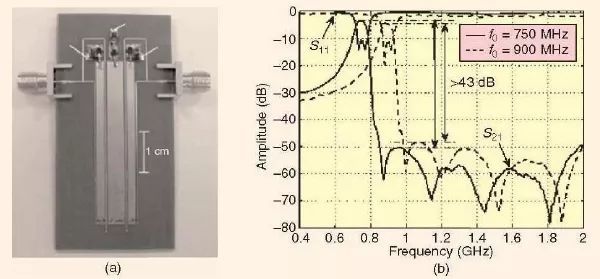
​图3、(a) 所制作的采用源/负载多谐振器耦合的3-极点电调梳状滤波器和(b)它的测量响应[9]。

射频微机电系统可重构滤波器

采用射频微机电系统可重构滤波器而不是变容器来改变谐振器滤波器中谐振器的长度或其电路参数则形成了第二类可重构滤波器[10]-[15]。在这种情况下，电子调谐通常是采用数字方法来实现的，这种方法可以实现具有良好性能的大的调谐范围，这包含了低损耗和高线性度。图4 展示了一个这种类型的滤波器的例子。在这种情况下，正如文献[11]中所报道的，这种拓扑结构是基于分布式半波长微带线谐振器上的，而这种谐振器则是在高阻性硅基片上制作的。这是一个具有两个谐振器的带通滤波器，在每一个谐振器的末端添加一个容性贴片，这便允许低损耗地实现一个伪2-比特（pseudo 2-bits）中心频率的移动。测量得到的滤波器响应示于图4（b）中，其中通带可以在四个不同的中心频率处进行重构。

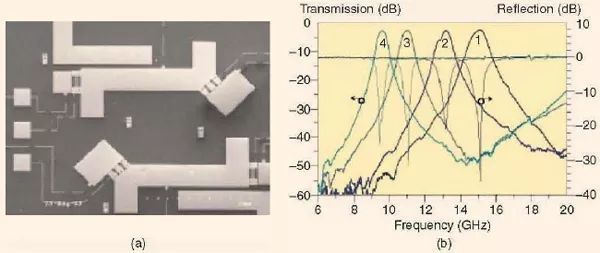
​图4、（a）一个2-比特射频微机电系统可重构滤波器的照片和（b）它所测得的响应[11]。

文献[13]中报道了在差分4-比特射频微机电系统可调谐滤波器方面所进行的开创性的工作。这个滤波器展示出极其微细的调谐精度，可在6.5 到10GHz 之间进行宽调谐范围的滤波，具有16 个频率上彼此相邻的不同的滤波响应，类似于一个连续可调谐滤波器。要了解更多有关射频微机电系统可重构滤波器的信息，请参考本杂志中专注于这个论题的文章[16]。

压电传感器可调谐滤波器

压电传感器（PET）也已经同样被用来开发电调微带线滤波器[17]-[19]。图5 对一个PET 可调谐微带线滤波器的构建进行了说明。正如在文献[17]中所报道的，这个可调谐滤波器电路包含有采用级联微带线开环谐振器[20]所组成的滤波器，一个PET 和一个在滤波器上方所附着的一个电介质微扰器。PET 是由铅（lead），锆酸盐(Zirconate)和钛酸盐(Titanate)组成的。图5 所示的PET是由两个压电层和一个垫片层组成的。夹在两个同样极化的压电层之间的垫片层增加了机械强度和硬度。垫片连接到直流电压的一个电极上来使PET 发生偏移，并且使之上下垂直运动。正如我们在图5 的结构中所能看到的，当微扰器上下运动时，滤波器的有效介电常数便会分别降低或增加，从而使得滤波器的通带向较高频率或较低频率处移动。

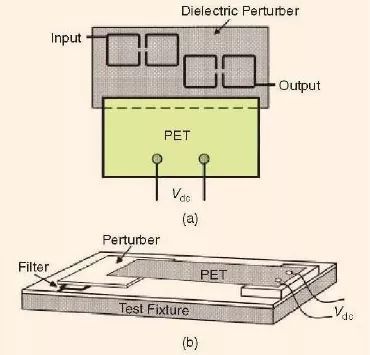
​图5、可调谐带通滤波器的构建[17]。（a）顶视图。（b）三维视图。

可重构UWB 滤波器

具有可切换陷波的UWB滤波器

图6 是所开发的具有可切换陷波频段的UWB 带通滤波器的图片[24]。从根本上说，没有陷波的UWB 滤波器是一个最佳的分布式高通滤波器，它在微带线上含有5段短路截线和四段连接线段[1]。

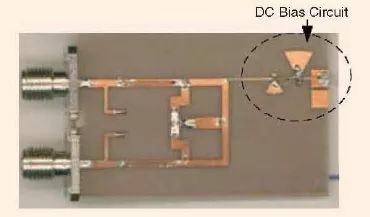
​图6、具有两个可切换陷波结构的微带线UWB 滤波器[24]。

为了在UWB 滤波器的通带上实现一个可切换的陷波，如图7 所示。两个完全相同的可切换陷波结构被集成进入两条连接线段中。这个结构中增加了一个宽带直流偏置电路。从原理上讲，图7 中的可切换陷波结构是一段具有一个镶嵌截线的传输线[39]。当p-i-n 二极管处于零偏置状态时，由于其非常小的结电容而呈现出一个很大的阻抗，因此镶嵌截线的作用便是一个可以产生谐振的开路截线。因此，在其基频谐振频率上，镶嵌的开路截线在主传输线上显示出短路的特性，从而产生一个窄的陷波频段或者说是频率响应中的陷波。这种情况对应的是陷波接通的状态。为了关闭陷波，一个正向偏置被施加到p-i-n 二极管上。在正向偏置下，p-i-n 二极管相当于一个很小的电阻。因此，镶嵌截线的开路端是与主传输线相连的，从而，没有来自于这个镶嵌截线的谐振。因此，陷波便会消失。

​图7、一个可切换陷波结构的示意图[24]。

图8 展示了可重构UWB 滤波器仿真和测量的响应，其中，我们可以观察到在中心频率约为5.1GHz 处的陷波的接通/关闭，当其接通时，其抑制比大于35dB。为了接通陷波，p-i-n 二极管（M/A-COM MA 4AGSBP907）是处于零偏置状态。当关闭陷波时，滤波器的性能与当p-i-n 二极管处于2.5-5mA 的正向偏置状态下的性能来说几乎是一样的。所测得的最小插入损耗为0.5dB，并且测量得到的3dB 带宽为5.92GHz。仿真和测量结果之间很小的差异可以解释为是由制造公差，p-i-n 二极管，芯片电感或电容的杂散效应所引起的。

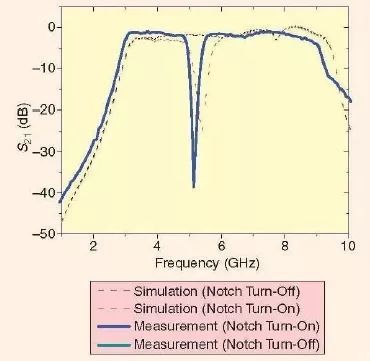
​图8、仿真和测量结果的比较[24]。（电磁(EM)仿真是使用商业化的工具得到的[40]。）

具有可调谐陷波的UWB 滤波器

在图6 中，人们用变容二极管来替代p-i-n 二极管便可以产生一个可调谐陷波结构。因此，前面所讨论的可重构UWB 滤波器可以进行修改，从而具有一个可进行电子调谐的陷波频段。所采用的是M/A-COM 公司的具有恒定伽玛值的GaAs 倒装芯片变容二极管[25]。图9（a）展示了MA46H120 变容二极管典型的性能曲线。为了进行实验演示，具有可调谐陷波的UWB 滤波器是在液晶聚合物上（LCD）实现的，基片的相对介电常数为3.0，厚度为0.5mm。图9(b)是所制作的滤波器。除了用变容二极管来替代p-i-n 二极管外，其版图设计与图6 的类似。变容二极管是通过一个10kΩ 电阻与直流电压相连接的。

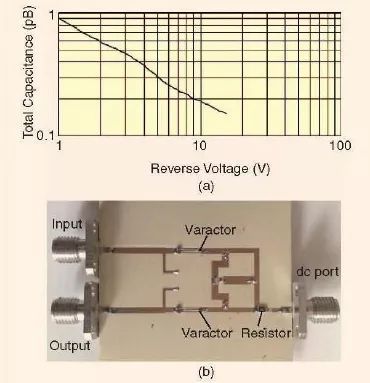
​图9、（a）MA46H120 变容二极管典型的性能。（b）采用MA46H120 变容二极管所制作的具有可调谐陷波的可重构超宽带滤波器[25]。

图10 是所测得的可重构UWB 滤波器的响应。当没有直流偏置时（0V），在通带上没有陷波，如图10（a）所示。这是因为变容二极管电容在0-V 偏置下是如此之大，以至于它将陷波频段移动到了通带以下。当直流偏置在4V 到14V 时，陷波频率在UWB 通带内4.5GHz 到6.5GHz 范围内被调谐，如图10（b）所示。

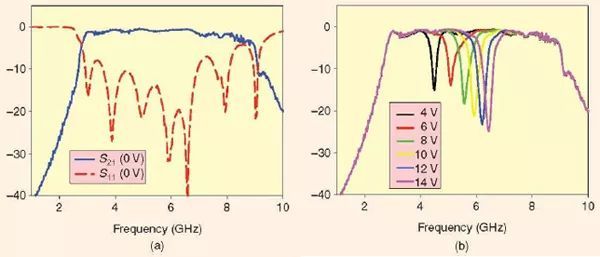
​图10、具有可调谐陷波频段的可重构超宽带滤波器所测得的性能。（a）没有陷波的0-V 偏置。（b）具有可调谐陷波的非零偏置（来源于[25]）。

具有槽线接地结构的BST 变容器调谐带阻滤波器

诸如BST 这类铁电体材料新近在用于频率捷变应用的电调微波电路的开发中变得更加吸引人[41]-[42]。接下来，我们要介绍最新开发的BST 变容器可调谐带阻滤波器[28]。

BST 变容器

BST 变容器的电容可调谐能力可以定义为

电容可调谐能力=

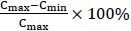(1)

其中Cmax是BST 变容器在0-V 偏置下的电容，Cmin 是在非零直流偏置下所获得的电容。当直流偏置电压的绝对值提高时，Cmin 会有所降低，这是因为BST 材料的相对介电常数是随着所施加的电压而减小的[42]。

一般来说，BST 变容器可以设计成金属-绝缘体-金属电容器的形式，或一种叉指电容器（IDC）的形式。BST 可调谐IDC 由于其额外的对直流电压不甚敏感的边缘电容而具有较小的电容可调谐能力。图11 说明了BST IDC 典型的特性[2]，当要求具有较低的电容值以及比较简单的制造工艺时，BST 可调谐IDC 便是一个更具有吸引力的选择。

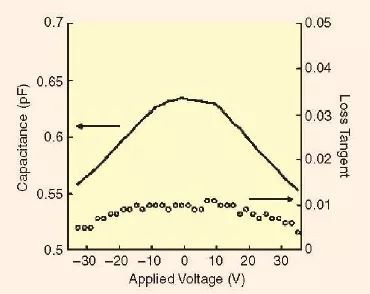
​图11、钛酸锶钡叉指电容变容器在1MHz 下的标称调谐曲线（有20 个叉指，每个叉指宽为5μm，长为100 μm，叉指间距为5μm）[2]。

正如在文献[28]中所公布的，IDC BST 变容器是在图12（a）所示结构的基础上制作的。通过脉冲激光沉积法将一层0.5-μm 厚的Ba0.5Sr0.5TiO3 （BST）薄膜沉积到一个（001）MgO 基片上（厚度为0.5-mm），在有氧环境下（0.1mbar）采用具有1.5Jcm-2 的激光以5Hz 的注入脉冲速度进行沉积[42]。所制成的BST 材料在电场强度从3.5 变化到0V/μm 时，相对介电常数从700 变化到1,200，所测得的BST 薄膜的介电损耗tanδ 在10MHz 下从0.1 变化到0.2。

图12（b）展示了具有六个叉指的IDC，这是文献[28]中所开发的BST 变容器的基本单元。彼此间距为10μm 的叉指为220-μm 长，10-μm宽。这个基本BST 变容器单元在0-V 偏置下的Cmax=0.56pF，在35-V 偏置下的Cmin=0.4pF，根据式（1），它在给定的直流偏置电压范围中的电容可调能力为28.6%。为了实际应用起见，人们制作了一个大的BST 变容器芯片，这个芯片可以很容易地附着在传统的微波电路板上。其尺寸为5×5mm2，含有三个并联的BST 变容器单元。

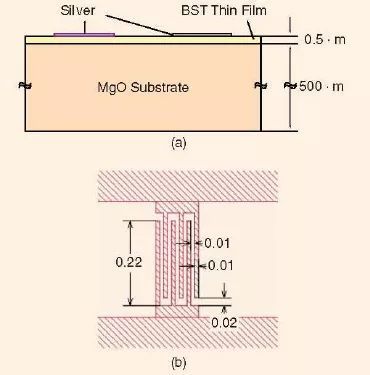
​图12、（a）在MgO 基片上所制作的钛酸锶钡叉指变容器芯片的剖面层。（b）钛酸锶钡叉指变容器单元的版图（尺寸单位为mm）[资料来源于28]。

可调谐带阻滤波器

图13 展示了一个具有槽线接地结构的两极点可调谐带阻滤波器。在接地平面上，可调谐微带线带阻滤波器包含两个可调谐BST 槽线谐振器和向BST 变容器提供直流电压的偏置电路。

​图13、制作成的采用钛酸锶钡变容器的可调谐微带线带阻滤波器[28]。（a）底部和（b）顶部。

图14 给出了可调谐微带线带阻滤波器的测量响应；这个带阻滤波工作在中心频率为1.2-1.4GHz 处，具有100MHz 的带宽。因此，所测得的调谐范围是14%。

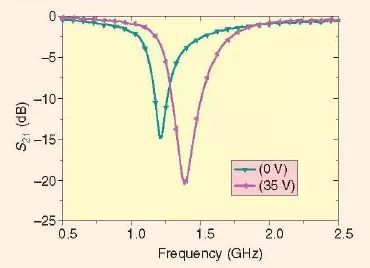
​图14、可调谐带阻滤波器的测量结果[28]。

可重构双模带通滤波器

人们可以在单模或双模谐振器的基础上设计带通滤波器，并且倾向于在微带线上进行设计，因为直流偏置电路可以很容易地在微带线上实施。双模微带线谐振器是很有吸引力的，因为每个双模谐振器可以被用作双调谐谐振电路，因此，给定了阶数的滤波器所需的谐振器的数量可以减半，从而可以产生一个紧凑的滤波器架构。对于一个传统的双模滤波器来说，两种简并的模式是通过控制一个合适的扰动而进行耦合的。环形滤波器（Circular ring filter）[43]，方形环路滤波器（Square loop filter），以及弯折环路滤波器（meander loop filter）[45]便属于这种情况。另一方面，在文献[46]中人们研究了一种新型的基于三角形贴片基础之上的双模谐振器滤波器，其中并未对双模进行耦合。最近，人们已经在一个小型的双模微带线开环滤波器中展示了这种独特且有趣的特性[47]，这种谐振器是由传统的单模开环谐振器演变而来的[20]。

当具有两维对称性的传统双模谐振器被用于双模带通滤波器的设计之中时，需要一些扰动来将两种简并的模式分开[1]。而在文献[46]和[47]中所介绍的双模谐振器则并不需要这个扰动，因为其两种分别被称为偶模和奇模的谐振模式彼此并不相互耦合。这两种模式会在双模滤波器中分开的频率上工作，其耦合结构是与传输的双模滤波器的耦合结构有所不同的。图15 展示了这种类型的一个两极点双模滤波器的耦合结构，其中S 和L分别代表着输入和输出端口；节点1 代表着奇模，节点2 代表着偶模。文献[46]和[47]中演示了具有固定中心频率的这种类型的滤波器。

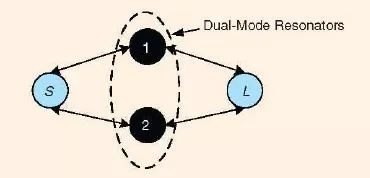
​图15、一个两极点双模滤波器的耦合结构，其中这两个模式彼此之间是没有耦合的[35]。

在文献[34]-[36]中，人们同样研究了电子可重构双模微带线开环谐振器滤波器，这种滤波器发掘了在单个双模谐振器中的两个谐振模式之间无耦合的独特特性。这便产生了一个简单的调谐方案，因为通带频率的调谐仅仅通过按比例改变模态频率便可完成。此外，对于这种类型的滤波器来说，其选择性可以通过电子方式重新设置，从而在通带的任何一边都会展示出具有一个有限频率传输零点的较高的选择性。

具有两个直流偏置的可重构双模滤波器

正如在文献[34]中所讨论的，图16 所显示的是制作成的两极点可重构双模微带线开环谐振器带通滤波器。

​图16、制作成的具有两个直流偏置的可重构双模微带线开环谐振器带通滤波器[34]。

这个带通滤波器具有如图15 所示的耦合方案。由于在两种工作谐振模式之间不存在耦合，因此，如果奇模和偶模的谐振频率是按比例移动的话，便可以调谐通带的中心频率。人们所采用的典型的可变电容在0.5pF到6.6pF 之间变化的Infineon BB857 变容器来实施这种电子调谐。为了能重构滤波器的特性，人们采用了两个直流偏置。第一个直流偏置电压V1 被用来改变奇模频率，第二个直流偏置电压V2被用来改变偶模频率。

测量得到的频率响应绘制在图17 中，这个频率响应展现出，取决于两个直流偏置的组合情况，人们不仅可以调谐通带频率，而且滤波特性也同样可以重构，从第一种情况下的通带高频一边具有高的选择性而改变为第二种情况下，通带的低频一边具有高的选择性。

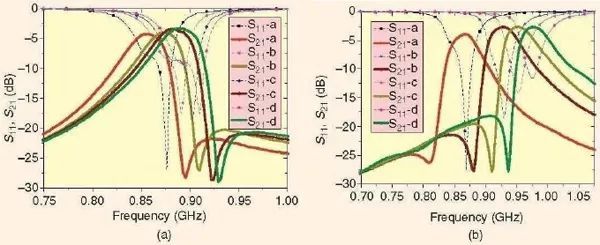
图17、具有两个直流偏置的可重构双模滤波器的测量性能。（a）第一种情况。（b）第二种情况[34]。

具有单个直流偏置的可调谐双模滤波器

通过改变双模微带线开环谐振器，双模滤波器的中心频率可以通过采用单个直流偏置来进行电子调谐。换句话说，偶模和奇模谐振频率的改变由于使用同样的偏置电压而变得更为简便。图18（a）展示了这种可调谐滤波器的一个例子[35]。这个滤波器是在相对介电常数为10.8 且厚度为1.27mm 的基础上制作的。这个滤波器上连接了三只Infineon BB857 变容器，这与上一种情况类似。变容器馈入的是同样的直流偏置电压。图18（b）展现出当直流偏置电压从8.1V 变化到25V 时所测得的频率响应。这个滤波器在通带的高端处展现了一个有限频率的传输零点，其中心频率的调谐范围是100MHz，在825 到925MHz 之间。在这种情况下，在滤波器进行调谐时，偶模频率总是高于奇模频率[46]。

​图18、（a）制作成的采用单个直流偏置，在通带高端处含有一个有限频率传输零点的可调谐双模滤波器。（b）所测得的频率响应[35]。（ 图片版权©European Microwave Association，EuMA。经许可使用。）

人们还可以采用另一种修改方案，文献[35]便展示了用单个直流偏置进行调谐，在通带的低端处具有一个有限频率的传输零点的可调谐双模滤波器。

可调谐四极点双模滤波器

可以将两个或多个双模，开环谐振器进行级联来构建一个具有较高阶数的可调谐滤波器。例如，图19 显示了一个制作成的这种类型的四极点可调谐滤波器[36]。每个双模开环谐振器加载了三个Infineon BB857 变容器。整个滤波器是用单个直流偏置电路来调谐的。直流偏置在10.6V 到34.0V 的范围内变化时的测量结果绘制在图20 中，并与加载了不同的变容器电容值的仿真结果进行了比较。

​图19、制作成的四极点可调谐双模滤波器[36]。（图片版权©European Microwave Association，EuMA。经许可使用。）

图20 展示了实验用四极点可调谐带通滤波器在通带的每一边都具有一个有限频率传输零点的准椭圆函数响应。接近于通带低端处的传输零点是与第一个双模谐振器所固有的偶模相关联的，而靠近通带高端处的传输零点则是与第二个双模谐振器的偶模相关联的。因此，当偶模频率被调谐时，相关的传输零点也会作出相应的移动。对于给定的直流偏置电压范围，人们可以在0.86-0.96GHz 的调谐范围内对滤波器进行调谐。

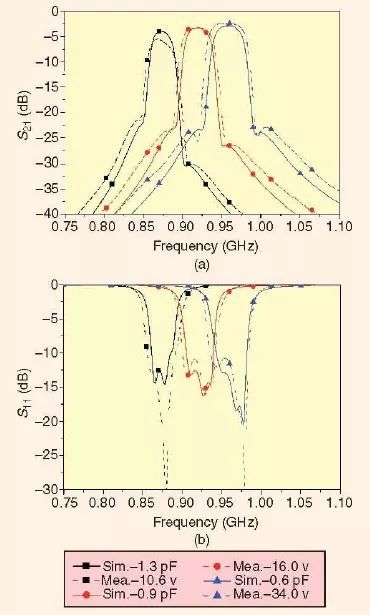
​图20、测量得到的可调谐滤波器的性能与仿真结果的比较。（a）S21 和（b）S11 [36]。

结论

本文介绍了若干种电子可重构或可调谐微带线滤波器。通过采用不同的电子控制技术，包括射频微机电系统和铁电体，梳状滤波器结构已经被广泛地用来开发可调谐或可重构滤波器，虽然这类滤波器的带宽通常都很小。本文所展示的UWB 滤波器采用的是p-i-n 二极管，但人们还实施了其它可切换元件，如金属半导体场效应管（MESFET）开关。MESFET 开关具有较低的直流功耗，但都有较大的非线性失真。人们同样还可以考虑使用射频微机电系统[13]-[14]或PET[18]。

BST 变容器已被用于具有槽线接地结构的电调微带线带阻滤波器中。这些结构可以很方便地实施调谐元件和直流偏置电路，使之与基片另一面的主要射频信号路径具有更好的隔离性。铁电体薄膜调谐器件，如BST 变容器在较高频率应用中是很有吸引力的，虽然其损耗需要被减到最小程度。

我们已经展示出一个可以通过控制奇模和偶模的谐振频率这种简单方式来调谐或者说进行电子重构的双模微带线开环谐振器滤波器，因为这两种操作模式彼此之间不存在耦合。

除了半导体变容器外，人们还实施了其它类型的变容器和技术，如铁电体薄膜和射频微机电系统变容器。一个类似的调谐技术可以被应用于较高阶数的滤波器中，在一个具有准椭圆函数响应的电调四极点双模微带线开环谐振器滤波器中已经演示了这种技术。通过选择合适的变容二极管并且合理地设计输入和输出馈电结构，便可以提高频率调谐范围。采用额外的调谐元件来控制输入和输出耦合，对滤波器带宽进行调谐也同样是可行的。

总的来说，带宽的调谐或控制比频率的调谐更加具有挑战性，具有较大带宽的电调滤波器的设计就调谐范围和带宽控制来说比窄带宽的更加困难。文献[48]-[51]中报道了一些在可调谐滤波器中进行带宽控制的技术。

电子可重构滤波器的非线性行为非常依赖于所使用的调谐元件。采用射频微机电系统和PET 通常会产生一个较好的线性特性。可重构滤波器设计中的创新同样可以改善性能并且能增加功能。调谐元件相对较低的Q 值会限制较高阶数和窄带可调谐滤波器的实施。这是因为，对于给定Q 值的调谐元件和其它与电路相关联的损耗来说，滤波器的插入损耗是随着其阶数的增高和带宽的降低而增加的。因此，高阶可调谐窄带滤波器的插入损耗对于实际应用来说是太大了。此外，调谐范围在高阶滤波器的限制比低阶滤波器的限制更大[4]。

可重构滤波器的开发涉及到一些折衷之处，例如滤波器的尺寸和偏置电路的复杂性，这些都增加了挑战性。可以设想在开发电子可重构微带线滤波器方面将会有更多的研究和开发活动。有众多文献都涉及到这个论题，其中一些被列入参考文献之中，感兴趣的读者可以参考这些文献以获取跟多的资讯。

致谢

本文所介绍的一些工作是由U.K.Engineering and Physical Science Research Council 通过两个研究项目（EP/C520289/1 ）和（EP/E02923/1）给予资助的。作者对参与这些项目的组织和个人表示感谢。

参考文献

[1] J.-S. Hong and M. J. Lancaster, Microstrip Filters for RF/Microwave Applications. New York: Wiley, 2001.

[2] J. Nath, D. Ghosh, J.-P. Maria, A. I. Kingon, W. Fathelbab, P. D. Franzon, and M. B. Steer, “An electronically tunable microstrip bandpass filter using thin-film barium-strontium-titanate (BST) varactors,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 9, pp.2707–2712, Sept. 1982.

[3] J. Sigman, C. D. Nordquist, P. G. Clem, G. M. Kraus, and P. S. Finnegan, “Voltage-controlled Ku-band and X-band tunable combline filters using barium-strontium-titanate,” IEEE Microwave Wireless Compon. Lett., vol. 18, no. 9, pp. 593–595, Sept. 2008.

[4] I. Vendik, O. Vendik, V. Pleskachev, A. Svishchev, and R. Wordenweber, “Design of tunable ferroelectric filters with a constant fractional band width,” in IEEE MTT-S Int. Microwave Symp. Dig., May 2001, vol. 3, pp. 1461–1464.

[5] W. M. Fathelbab and M. B. Steer, “A reconfigurable bandpass filter for RF/microwave multifunctional systems,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 3, part 2, pp. 1111–1116, Mar. 2005.

[6] G. Torregrosa-Penalva, G. Lopez-Risueno, and J. I. Alonso, “A simple method to design wide-band electronically tunable combline filters,” IEEE Trans. Microwave Theory Tech., vol. 50, no. 1, part 1, pp.172–177, Jan. 2002.

[7] I. Vendik, O. Vendik, V. Pleskachev, and M. Nikol’ski, “Tunable microwave filters using ferroelectric materials,” IEEE Trans. Appl. Superconduct., vol. 13, no. 2, part 1, pp. 716–719, June 2003.

[8] B.-W. Kim and S.-W. Yun, “Varactor-tuned combline bandpass filter using step-impedance microstrip lines,” IEEE Trans. Microwave Theory Tech., vol. 52, no. 4, pp. 1279–1283, Apr. 2004.

[9] M. Sanchez-Renedo, “High-selectivity tunable planar combline filter with source/load-multiresonator coupling,” IEEE Microwave Wireless Compon. Lett., vol. 17, no. 7, pp. 513–515, July 2007.

[10] G. M. Kraus, C. L. Goldsmith, C. D. Nordquist, C. W. Dyck, P. S. Finnegan, F. Austin, IV, A. Muyshondt, and C. T. Sullivan, “A widely tunable RF MEMS end-coupled filter,” in 2004 IEEE MTT-S Int. Microwave Symp. Dig., June 6–11, 2004, vol. 2, pp. 429–432.

[11] P. Blondy, C. Palego, M. Houssini, A. Pothier, and A. Crunteanu, “RFMEMS reconfigurable filters on low loss substrates for flexible front ends,” in Proc. Asia-Pacific Microwave Conf. 2007 (APMC 2007), Dec. 11–14, 2007, pp. 1–3.

[12] A. Pothier, J.-C. Orlianges, G. Zheng, C. Champeaux, A. Catherinot, D. Cros, P. Blondy, and J. Papapolymerou, “Low-loss 2-bit tunable bandpass filters using MEMS dc contact switches,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 1, pp. 354–360, Jan. 2005.

[13] K. Entesari and G. M. Rebeiz, “A differential 4-bit 6.5-10-GHz RF MEMS tunable filter,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 3, part 2, pp. 1103–1110, Mar. 2005.

[14] I. C. Reines, C. L. Goldsmith, C. D. Nordquist, C. W. Dyck, G. M. Kraus, T. A. Plut, P. S. Finnegan, F. Austin, IV, and C. T. Sullivan, “A low loss RF MEMS Ku-band integrated switched filter bank,” IEEE Microwave Wireless Compon. Lett., vol. 15, no. 2, pp. 74–76, Feb. 2005.

[15] R. Zhang and R. R. Mansour, “Novel tunable lowpass filters using folded slots etched in the ground plane,” in 2005 IEEE MTT-S Int. Microwave Symp. Dig., June 12–17, 2005, pp. 775–778.

[16] G. M. Rebeiz, K. Entesari, I.C. Reines, S.-J. Park, M.A. El-Tanani, A. Grichener, and A.R. Brown, “Tuning in to RF MEMS,” IEEE Microwave Mag., vol. 10, no. 6, pp. 55–72, Oct. 2009.

[17] L.-H. Hsieh and K. Chang, “Tunable microstrip bandpass filters with two transmission zeros,” IEEE Trans. Microwave Theory Tech., vol. 51, no. 2, part 1, pp. 520–525, Feb. 2003.

[18] W.-T. Tu and K. Chang, “Piezoelectric transducer-controlled dualmode switchable bandpass filter,” IEEE Microwave Wireless Compon. Lett., vol. 17, no. 3, pp. 199–201, Mar. 2007.

[19] Y. Poplavko, D. Schmigin, V. Pashkov, M. Jeong, and S. Baik, “Tunable microstrip filter with piezo-moved ground electrode,” in Proc. 2005 European Microwave Conf., Oct. 4–6, 2005, vol. 2.

[20] J.-S. Hong and M. J. Lancaster, “Couplings of microstrip square openloop resonators for cross-coupled planar microwave filters,” IEEE Trans. Microwave Theory Tech., vol. 44, no. 11, pp. 2099–2109, Nov. 1996.

[21] S. Pal, C. Stevens, and D. Edwards, “Tunable HTS microstrip filters for microwave electronics,” Electron. Lett., vol. 41, no. 5, pp. 286–288, Mar. 2005.

[22] G. L. Matthaei, “Narrow-band, fixed-tuned, and tunable bandpass filters with zig-zag hairpin-comb resonators,” IEEE Trans. Microwave Theory Tech., vol. 51, no. 4, part 1, pp. 1214–1219, Apr. 2003.

[23] G. Subramanyam, F. W. Van Keuls, and F. A. Miranda, “A K bandfrequency agile microstrip bandpass filter using a thin-film HTS/ferroelectric/dielectric multilayer configuration,” IEEE Trans. Microwave Theory Tech., vol. 48, no. 4, part 1, pp. 525–530, Apr. 2000.

[24] Y.-H. Chun, H. Shaman, and J.-S. Hong, “Switchable embedded notch structure for UWB bandpass filter,” IEEE Microwave and Wireless Compon. Lett., vol. 18, no. 9, pp. 590–592, Sept. 2008.

[25] H. R. Arachchige, J.-S. Hong, and Z.-C. Hao, “UWB bandpass filter with tunable notch on liquid crystal polymer substrate,” in Proc. Asia-Pacific Microwave Conf. 2008 (APMC 2008), Dec. 16–20, 2008, pp. 1–4.

[26] E. E. Djoumessi, M. Chaker, and K. Wu, “Varactor-tuned quarterwavelength dual-bandpass filter,” IET Microwaves, Antennas Propagat., vol. 3, no. 1, pp. 117–124, Feb. 2009.

[27] D. R. Jachowski, “Compact, frequency-agile, absorptive bandstop filters,” in IEEE MTT-S Int. Microwave Symp. Dig., 2005, pp. 513–516.

[28] Y.-H. Chun, J.-S. Hong, P. Bao, T. J. Jackson, and M. J. Lancaster, “BST varactor tuned bandstop filter with slotted ground structure,” in Proc. 2008 IEEE MTT-S Int. Microwave Symp., June 2008, pp. 1115–1118.

[29] S. Y. Huang and Y. H. Lee, “A compact e-shaped patterned ground structure and its applications to tunable bandstop resonator,” IEEE Trans. Microwave Theory Tech., vol. 57, no. 3, pp. 657–666, Mar. 2009.

[30] Y.-H. Chun, J.-S. Hong, P. Bao, T. J. Jackson, and M. J. Lancaster, “An electronically tuned bandstop filter using BST varactors,” in Proc. 38th European Microwave Conf. 2008, EuMC 2008, Oct. 27–31, 2008, pp. 1699– 1702.

[31] W. D. Yan and R. R. Mansour, “Compact tunable bandstop filter integrated with large deflected actuators,” in Proc. 2007 IEEE/MTT-S Int. Microwave Symp., June 3–8, 2007, pp. 1611–1614.

[32] Y.-H. Chun, J.-S. Hong, P. Bao, T. J. Jackson, and M. J. Lancaster, “BSTvaractor tunable dual-mode filter using variable ZC transmission line,” IEEE Microwave Wireless Compon. Lett., vol. 18, no. 3, pp. 167–169, Mar. 2008.

[33] M. R. Al Mutairi, A. F. Sheta, and M. A. AlKanhal, “A novel reconfigurable dual-mode microstrip meander loop filter,” in Proc. 38th European Microwave Conf. 2008, EuMC 2008, Oct. 27–31, 2008, pp. 51–54.

[34] Y.-H. Chun and J.-S. Hong, “Electronically reconfigurable dualmode microstrip open-loop resonator filter,” IEEE Microwave Wireless Compon. Lett., vol. 18, no. 7, pp. 449–451, July 2008.

[35] W. Tang and J.-S. Hong, “Compact tunable microstrip bandpass filters with asymmetrical frequency response,” in Proc. 38th European Microwave Conference (EuMC2008), pp. 599–602. October 2009 IEEE microwave magazine 83

[36] W. Tang and J.–S. Hong, “Tunable microstrip quasi-elliptic function bandpass filters,” in Proc. 39th European Microwave Conf., 2009, Paper EuMC41-1.

[37] P. W. Wong and I. C. Hunter, “A new class of low-loss high-linearity electronically reconfigurable microwave filter,” IEEE Trans. Microwave Theory Tech., vol. 56, no. 8, pp. 1945–1953, Aug. 2008.

[38] P.W. Wong and I. Hunter, “Electronically tunable filters,” IEEE Microwave Mag., vol. 10, no. 6, pp. 46–54, Oct. 2009.

[39] H. Shaman and J.-S. Hong, “Ultra-wideband (UWB) bandpass filter with embedded band notch structures,” IEEE Microwave Wireless Compon. Lett., vol. 17, no. 3, pp. 193–195, Mar. 2007.

[40] EM User’s Manual, Version 10, Sonnet Software Inc., NY, 2006.

[41] F. A. Miranda, G. Subramanyam, F. W. van Keuls, R. R. Romanofsky, J. D. Warner, and C. H. Mueller, “Design and development of ferroelectric tunable microwave components for Ku and K-band satellite communication systems,” IEEE Trans. Microwave Theory Tech.,vol. MTT-48, no. 7, pp. 1181–1189, July 2000.

[42] P. M. Suherman, T. J. Jackson, Y. Y. Tse, I. P. Jones, R. I. Chakalova, and M. J. Lancaster, “Microwave properties of Ba0.5Sr0.5TiO3 thin film coplanar phase shifters,” J. Appl. Phys., vol. 99, no. 104101, pp. 1–7, May 2006.

[43] I. Wolff, “Microstrip bandpass filter using degenerate modes of a microstrip ring resonator,” Electron. Lett., vol. 8, no. 12, pp. 302–303, June 1972.

[44] J.-S. Hong and M. J. Lancaster, “Bandpass characteristics of new dualmode microstrip square loop resonators,” Electron. Lett., vol.31, no. 11, pp. 891–892, May 1995.

[45] J.-S. Hong and M. J. Lancaster, “Microstrip bandpass filter using degenerate modes of a novel meander loop resonator,” IEEE Microwave Guided Wave Lett., vol. 11, no. 5, pp. 371–372, Nov. 1995.

[46] J.-S. Hong and S. Li, “Theory and experiment of dual-mode microstrip triangular patch resonators and filters,” IEEE Trans. Microwave Theory Tech., vol. 52, no. 4, pp. 1237–1243, Apr. 2004.

[47] J.-S. Hong, H. Shaman, and Y. H. Chun, “Dual-mode microstrip open-loop resonators and filters,” IEEE Trans. Microwave Theory Tech., vol. 55, no. 8, pp. 1764–1770, Aug. 2007.

[48] W. L. Jones, “Design of tunable combline filters of near-constant bandwidth,” Electron. Lett., vol. 1, no. 6, pp. 156–158, Aug. 1965.

[49] B. E. Carey-Smith, P. A. Warr, M. A. Beach, and T. Nesimoglu, “Wide tuning-range planar filters using lumped-distributed coupled resonators,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 2, pp. 777–785, Feb. 2005.

[50] M. Sanchez-Renedo, R. Gomez-Garcia, J. I. Alonso, and C. Briso- Rodriguez, “Tunable combline filter with continuous control of center frequency and bandwidth,” IEEE Trans. Microwave Theory Tech., vol. 53, no. 1, pp. 191–199, Jan. 2005.

[51] M. Sanchez-Renedo and R. Gomez-Garcia, “Small-size planar tunable combline filter using decoupling walls,” Electron. Lett., vol. 43, no. 9, pp. 532– 534, Apr. 2007.

来源：IEEE microwave magazin 作者：Jia-Sheng Hong