微波场量子精密测量历史和里德堡原子微波电场精密测量原理

南京邮电大学智能芯片精密测量实验室 殷筱晗

近年来，基于原子精密谱的微波测量引起了极大关注，由此诞生了原子微波电场计、原子微波磁场计和原子微波功率标准等。原子微波探测技术是一种物理原理全新的技术，它把微波场强通过基本物理常量与频率测量直接联系起来，进而实现电磁量的国际单位制溯源。这种新型微波测量技术的最大优势在于不需要校准，且其理论测量灵敏度远高于传统电子微波测量技术。另一方面，为实现传统电子学中极为复杂甚至无法完成的宽带信号产生、控制和处理，以实现多功能、高精度、实时探测的雷达探测，科学家们发展了大带宽、低传输损耗、抗电磁干扰的微波光子学技术。本文尝试总结了包括原子微波电场计、原子微波磁场计、微波光子雷达在内的国内外微波场测量历史。微波磁场测量原理在此文中不再赘述，请参考南邮研究组之前的公众号推文，本文重点介绍微波电场计的原理和国内外进展。本文最后做了一些粗浅的展望，希望抛砖引玉，供国内从事相关研究的射频工程师一些参考。

一、微波场精密测量的历史

1.1 原子微波磁场计

①瑞士巴塞尔大学(University of Basel) Philipp Treutlein博士团队于2010年采用基态原子拉比振荡测量了施加于冷铷原子上的微波磁场^[1]；2012年，用二维热原子气室实现了350μm 分辨率的二维磁场探测；2015年用厚为6mm×6mm×140μm 的超薄二维微加工气室将成像空间分辨率提高至100μm 以内，在50μm×50μm×140μm 体元内探测灵敏度达到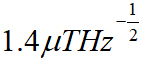；2016年演示了频率可调的场探测，通过施加0.8T的静磁场将可探测的微波场频率提高至约26.4GHz。作者在原理性验证装置中实现了18GHz微波磁场测量准确度约为10％，并指出通过采用更小气室，测量有望达到10^-3量级的准确度^[2]。

②瑞士纳沙泰尔大学(University of Neuchatel) G. Mileti教授团队与P. Treutlein博士团队合作，对小型铷原子钟磁控管型谐振腔内的微波磁场强度分布进行了测量。2015年报道的结果显示微波磁场测量空间分辨率小于100μm，6.8GHz微波磁场振幅测量不确定度＜3％（＜8nT），为分析和改进气室型原子钟性能提供了帮助^[3,4]。

③2019年，E. K. Dietsche, A. Larrouy, S. Haroche1, J. M. Raimond1,M. Brune1, S. Gleyzes团队报告了一种基于里德堡电平的高灵敏度单原子磁力计的实现，其n≈50。它依赖于一个量子干涉过程，涉及两个具有相反磁矩的圆形状态的叠加|nC^＋>和|nC^->，通过量子态工程在铷原子的斯塔克歧管中制备。从经典的角度来说，这种状态对应于一个电子在0.3μm直径的圆形轨迹上同时向两个相反的方向运行。根据对称性，这两种状态经历了完全一样的斯塔克效应。这种敏感的磁场探测因此完全不受电扰动的影响，从而导致一个叠加的相干时间长^[5]。

1.2 原子微波电场计

①  美国俄克拉荷马大学(University of Oklahama) J. P. Shaffer教授团队于2012年在国际上首次报道了里德堡原子微波电场计^[6,7]，实现的微波电场测量灵敏度达到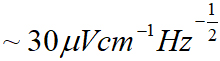，可探测的最小场强约为8μVcm^-1。同时指出理论上可探测弱于100nVcm^-1的微波电场，目前探测能力受限于探测光和耦合激光的频率和功率稳定性；2013年，首次演示了矢量电场计，实验测量显示微波电场偏振分辨率为0.5°；2014年首次将该传感技术用于微波电场成像，结果在6.9 GHz上的成像空间分辨率为66μm (~λ/650)；2015年分析了原子气室的结构对电场测量的影响；2016年和2017年又分别采用基于Mach-Zehnder干涉仪的零差探测技术和频率调制技术改进了测量，目前该团队已将微波电场探测灵敏度优化至。

②  美国国家标准技术研究院（National Institute of Standards and Technology，NIST）则更多地开展了里德堡电场计的创新应用，把可探测场推进至毫米波，甚至是太赫兹波段。如，2014年NIST组对频率为104.77GHz的电场进行了测量成像，空间分辨率≈100μm ^[8,9]；2016年用铷铯混合气室实现了两个EIT信号同步探测，研究表明封闭在同一气室中的两种元素可以充当两个独立的场探测器，同期还利用频率失谐方法提高电场测量灵敏度；作为计量机构，NIST科学家开展原子微波测量研究的目标是建立基于量子的新电磁标准，为此，2017年该团队对影响电场测量的因素予以了细致分析。他们将测量不确定度来源分为与量子相关和与微波相关两个方面，其中量子不确定度主要来自于电偶极矩，误差为0.1％；目前与微波相关的不确定度是这一探测技术不确定度的主要来源，而微波不确定度的最大来源则是承载原子的介电气室。

③  美国密歇根大学(University of Michigan) G. Raithel教授团队重点研究了微波强电场测量。在弱场（近似1mV/m到几十V/m）单光子跃迁情况下，原子和微波场互作用强度比里德堡能级结构小，能级频移可用扰动理论来描述。此时，拉比频率是功率平方根的线性函数，电场强度可直接由里德堡EIT线的AT分裂宽度得到；而在强场下，原子响应变得高度非线性，为此G. Raithel教授团队借助无扰动弗洛奎模型来分析里德堡能级移动和激发速率。作为示例，2016年研究报道了微波辐射场达到目标双光子65D~66D里德堡态微波离子化率20％(230V/m)时的里德堡EIT系统响应，绝对强场测量准确度为6％^[10]；2017年又报道了连续波强电场测量，在Ka波段实现了±1GHz带宽、~230V/m→1kV/m场强的测量^[11]。

④  中国山西大学(Shanxi University)物理学科科研团队在基于原子体系的微波精密测量研究中取得了突破性进展，由贾锁堂教授和肖连团教授带头的激光光谱研究团队，在国际上首次实现里德堡原子微波超外差接收机样机^[12]，极大提升了微波电场场强的探测灵敏度，微波测量灵敏度达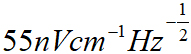，优于之前国际最好水平1000倍，最小可探测微波场强约400pV/cm，优于之前国际最好水平10000倍。

⑤南京航空航天大学(Nanjing University of Aeronautics and Astronautics)的史经展、张方正、贲德、潘时龙教授于2020年提出了一种光子辅助的单系统，用于在大光谱范围内测量微波信号的频率和相位噪声^[13]。要测量的频率和相位噪声均从被测信号与其副本之间的相位差中提取，该相位差被光纤和可变光延迟线（VODL）所延迟。系统校准、频率测量和相位噪声测量是通过在不同的工作模式下调整VODL来执行的。实验证明了在5至50 GHz较大频率范围内对微波信号的准确频率和相位噪声测量。

1.3 微波光子雷达^[14]

①早在20世纪80年代末，美国DARPA就开始支持微波光子雷达相关的研究，并将微波光子学在雷达系统中的应用分3个阶段。第1阶段开展高线性模拟光链路的研究，利用超低损耗的光纤（传输损耗仅有0.0002 dB/m）取代传统微波雷达接收前端中体积大、质量大、损耗大和易被电磁干扰的同轴电缆，这个阶段的典型成果为20世纪70年代末美国莫哈韦沙漠中的“深空网络”。第2阶段的目标是实现光控（真延时）波束形成网络，用于替代在宽带情况下会出现波束倾斜、孔径渡越等问题的传统相移波束形成网络，这个阶段的典型成果是1994 年美国休斯飞机公司（Hughes Aircraft）实现的基于光纤波束形成网络的宽带共形阵列。进入21世纪后，随着光纤通信的蓬勃发展，光子技术越来越成熟，光电转换效率不断提升，微波光子技术也得到了飞速发展。因而，美国DARPA将微波光子雷达研究第3阶段目标定为微波光子信号处理的实现，期望研制出芯片化的微波光子雷达射频前端，目前不少项目及其衍生项目还在执行中。

②不同于美国，欧盟更加关注微波光子雷达系统的研究。世界十大防务集团之一——意大利芬梅卡尼卡集团认为微波光子雷达系统的发展要分4步走。第1步，采用光子技术辅助射频功能的完成，主要包括利用光纤进行射频信号的远距离传输等；第2步，采用光子完成复杂的射频功能，包括高频高稳高纯微波信号的光学产生，利用光子技术进行微波信号的移相滤波变频采样等处理；第3步，光子技术取代部分电技术在雷达系统中发挥作用，主要涉及光控波束形成在部分雷达系统中的应用；第4步，采用光子技术构建雷达系统，亦即实现全光的雷达收发样机。欧盟第1次在雷达系统中测试微波光子技术要追溯到1996年欧洲最大防务电子集团——泰勒斯（Thales）集团完成的光控相控阵样机。2013年，意大利国家光子网络实验室的Bogoni团队完成了1个结合微波光子多载波产生、发射和接收的光子雷达收发信机PHODIR。2015年，Bogoni研究组对系统进行了改进，将PHODIR雷达拓展至双波段，还研究了雷达/通信双用途原型机。

③俄罗斯也一直在发展微波光子雷达技术。2014年俄罗斯最大的无线电子设备制造商无线电电子技术联合集团（KRET）开展“射频光子相控阵”（ROFAR）项目研究。该项目旨在开发基于光子技术的通用技术和核心器件，制造射频光子相控阵样机，用于下一代雷达和电子战系统。ROFAR 采用分布式系统，可以发射带宽高达100 GHz的信号，发射机能效大于60%，可以对几百km外的物体实现3D成像。相对于传统雷达，ROFAR雷达的系统质量降低50%，分辨率可以提升数10倍。

④国内微波光子雷达的研究可以追溯至21世纪初，虽然相比美国和欧盟起步略晚，但发展极为迅速。2013年南京航空航天大学成立了雷达成像与微波光子技术教育部重点实验室，先后开展了基于光纤连接的分布式雷达、超宽带噪声雷达、无源雷达等雷达系统研究。2017年6月，南京航空航天大学联合中国电子科技集团第14研究所研制出了可实现小目标实时成像的微波光子雷达验证系统^[15]。该系统利用微波光子技术对接收信号进行预处理，在不损失信息量的前提下极大地压缩了数据量，成功实现了对小尺寸目标的实时高分辨成像，成像精度优于2 cm。此技术突破了电子技术对带宽与处理速度的限制，能为高精度实时雷达目标监测提供可靠的技术支持。同期，中国科学院电子学研究所微波成像技术国家重点实验室的研究团队也完成了基于微波光子技术的SAR成像研究，其雷达发射信号带宽为600 MHz，对应成像分辨率25 cm。该系统实现了大型非合作目标波音737的成像，有效论证了微波光子雷达的可行性。清华大学也报道了一种用于测距和成像的光子雷达系统，该系统利用1个4位光数模转换器（DAC）产生了1个中心频率10 GHz，带宽4 GHz的线性调频信号，经发射天线发射、目标反射及接收天线接收后，携带上目标的距离和速度等信息。该光子雷达系统的距离精度为5 cm，测速精度为2 m/s。此外，2015年上海交通大学还报道了基于锁模激光器的光子雷达系统，用于测距。

二、里德堡精密测量微波电场

南京邮电大学智能芯片精密测量实验室已经就芯片表面微波磁场的精密测量的原理在公众号里做了比较详细的介绍。下面，我们就以上三个方向中的原子微波电场计技术展开，具体介绍中国山西大学激光光谱研究团队在里德堡精密测量微波电场方面取得的突破。

2.1 测量原理

根据图1所示产生一个里德堡原子超外差。关键的新成分是和里德堡转换发生共振的局部强微波场，拉比频率为Ω_L 。目标是测量在里德堡状态间产生频率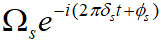的信号微波，其中Ω_S <<Ω_L，频率去谐δ_S 和相位Φ_S 都是相对于其局部场测量的。考虑2πδ_S <<Γ_EIT ，其中Γ_EIT 为典型EIT线宽。

 

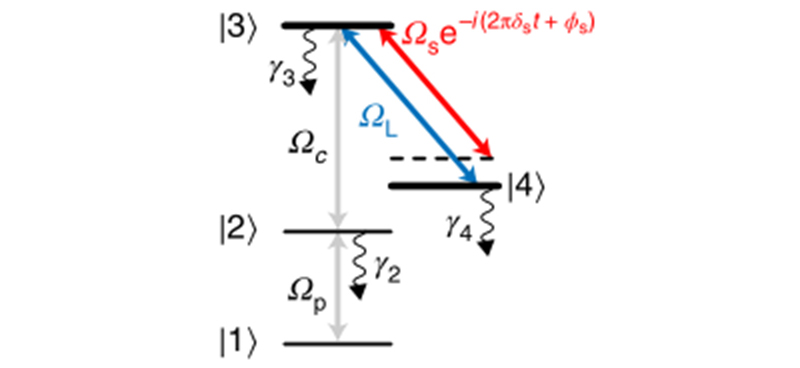
图1 里德堡原子态

在原子超外差中，微波信号中的全部信息被编码在微波处理的里德堡态的一阶能量位移中。强共振局域微波场导致两种处理后的状态|±>被ηΩ_L 分开，其中η为普朗克常量，它们分别是两个裸里德堡态|3>和|4>的对称和反对称叠加。当其被一个小微波信号扰动时，|±>需要一瞬间的能量变换±E _l =±ηΩ_S cos(2πδ_S t+Φ_S )/2。

在探测E _l时，使用Ω_L 作为控制旋钮来控制里德堡原子的EIT光谱，如图2所示。由于强局域微波引起EIT峰的Autler-Townes（AT）分裂，共振透射点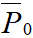的位置移到每条EIT线的倾斜段上，其斜率为|κ|。因此，当能量扰动±E _l使两条EIT线向外偏移时，这种偏移以的速率κ线性转移为共振光透射的变化。通过调节Ω_L ，可以修改EIT线的轮廓，从而有效地控制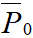在其中的位置（如图2）。这使得我们能够在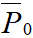位于两条EIT线的最大值的一半附近时获得最大斜率|κ₀|的最佳点。

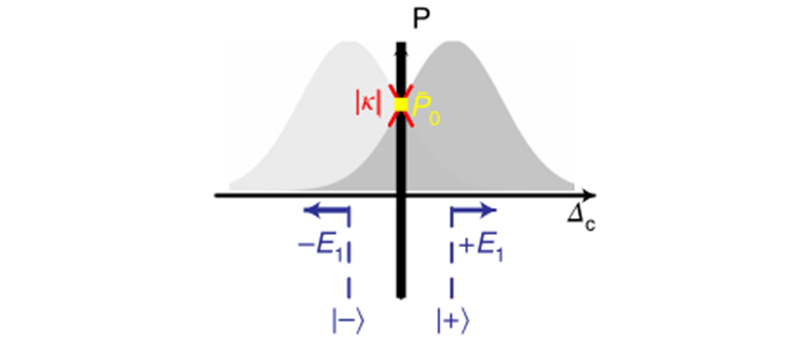
图2 微波处理的里德堡EIT光谱微波传感图

里德堡原子超外差因此检测到微波信号作为振荡光学读出，由有信号和无信号时共振光传输中的变化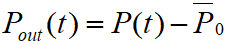表示，如图3所示。当在最佳点操作时，有：

P_out (t) = |P(δ_S )|cos(2πδ_St+Φ_S )（1）

此处，|P(f)|是在线性频率f下P(t)的单边傅里叶谱的振幅，信号的拉比频率Ω_S 由测量算出:

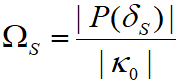（2）

这提供了信号振幅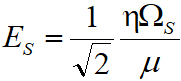，其中μ是与里德堡跃迁有关的偶极矩。整个过程使用的是均方根振幅。关键的是， |κ₀|和|P(δ_S )|都是直接从光谱中导出的，从而从根本上将电场测量简化为光学频率测量，并确保测量的SI可追溯性。

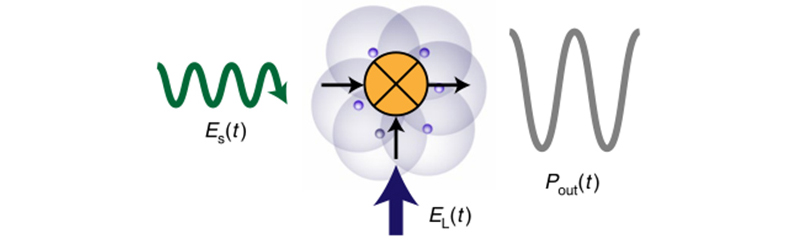
图3 测量原理图

公式（1）和（2）是基于原子超外差的微波传感的核心。在测量Ω_S <<Γ_EIT 区域的超弱电场方面，它比现有的原子微波传感器有显著的优势。在相位和频率分辨率方面，它也在可追踪的振幅测量中可观地提高了灵敏度。特别是，原子超外差的灵敏度具有有利的标度（S∝σ，其中σ为经典噪声引起的误差）和最小可探测场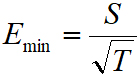（,其中T为测量时间）。这与标准原子电子计形成鲜明对比^[16-17]，其对于Ω_S <<Γ_EIT 实现非线性检测，其中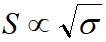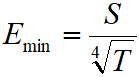，。结合在最优点的操作，原子超外差最大限度地提高了效率，以努力通过降低经典噪声来提高灵敏度，或者通过增加测量时间来进入更小的领域。

2.2 实验实现

在室温蒸气池使用Cs原子可实现里德堡原子超外差。下面提供了最佳点和线性关系的实验验证。扫描为局部微波场函数的|P(δ_S )|，其特点是它最大值的存在（如图4），说明存在一个最佳点。

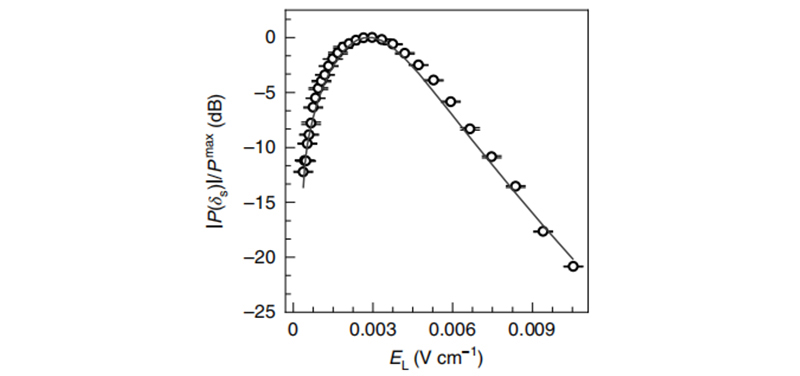
图4 局部微波场函数|P(δ_S )|曲线图

与此最大值相对应的EIT谱（如图5），与双峰拟合结合，表明谐振传输点确实位于每条EIT线的半最大值，或者说Ω_L～Γ_EIT 。

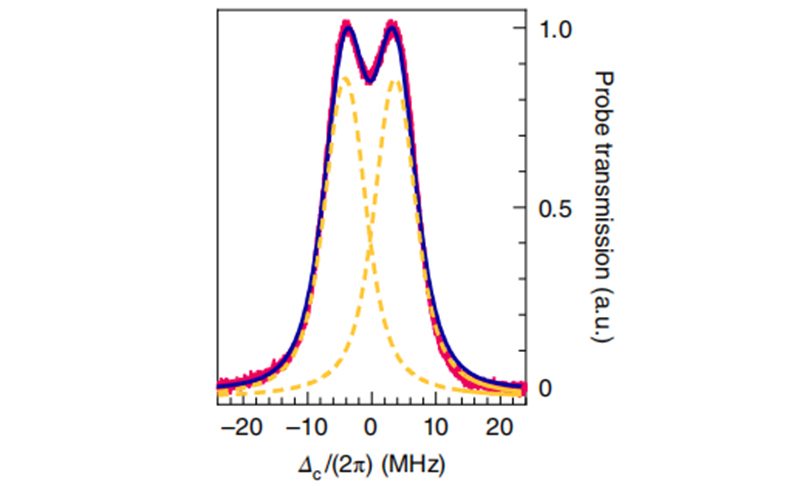
图5 与最大值相对应的EIT谱

图4和图5中的实心曲线代表了理论上的计算，与实验结果一致。图6印证了Ω_S <<Ω_L 时原子超外差的|P(δ_S )| ∝E _S的关系，但当Ω_S～Ω_L 时，线性开始被破坏。要在给定相同的光学读出噪声的情况下，在Ω_S <<Γ_EIT～Ω_L的体系中进一步说明线性检测比非线性检测的优势，将设置转换为原子的标准配置。然后发现其光输出（如图6）的比例正比于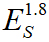（近乎二次方）与E _S的比例，达到了单位信噪比(SNR)，其E_S 值远大于原子超外差。要注意的是，对于Ω_S >Γ_EIT ，E _S的线性检测通过AT分裂测量是可行的。

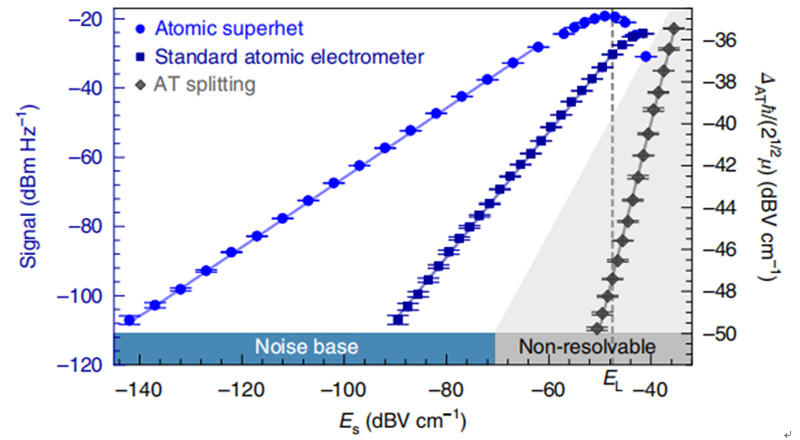
图6 不同设置下的光信号曲线

2.3 技术优势

在建立了传感原理之后，现在根据方程（1）和（2）证明原子超外差在微波测量中的卓越性能。从1s的测量时间内获得的电场E _S（如图7），可得出灵敏度为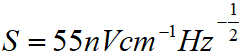，比传统技术提高了38倍。

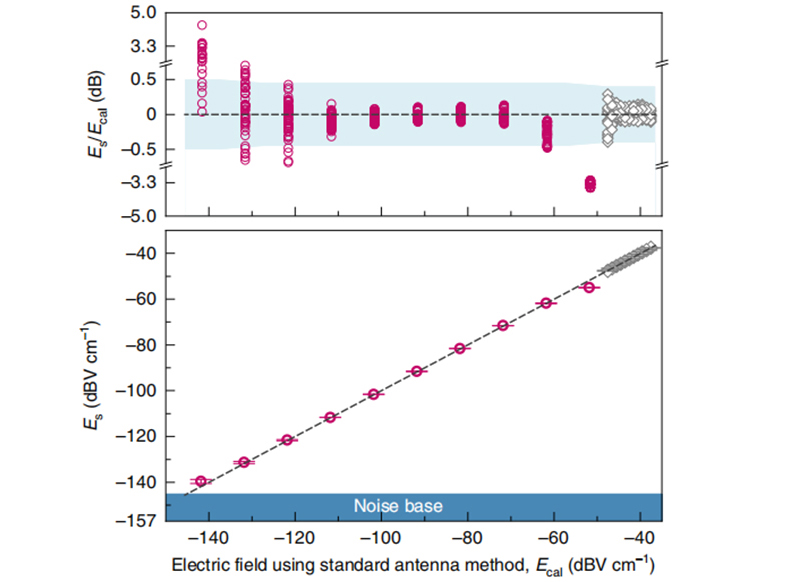
图7 1s的测量时间内获得的电场E_S

为找到可实现的最小的可测场E_min，要降低影响系统长期稳定性的噪声。在不同时间对同一信号的测量显示出一个随机信号在1%范围内波动到T=5000s（如图8），显示出系统在这段时间内的稳定性。测量的E _min(T)和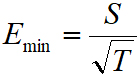相一致，符合预期。因此得到T=5000s时的E _min=780pVcm^-1。

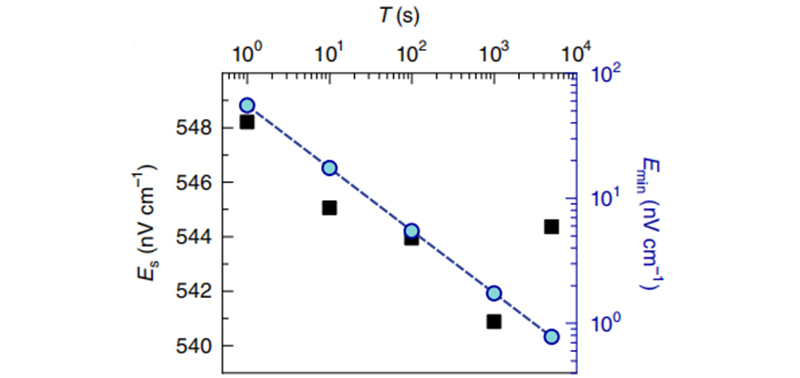
图8 E _S随时间的变化

图9显示了微波电场在T=5000s时的典型单边傅里叶频谱。因为T按原理受外部同步时钟稳定性的限制，可延长到4小时以上，预计达到。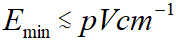

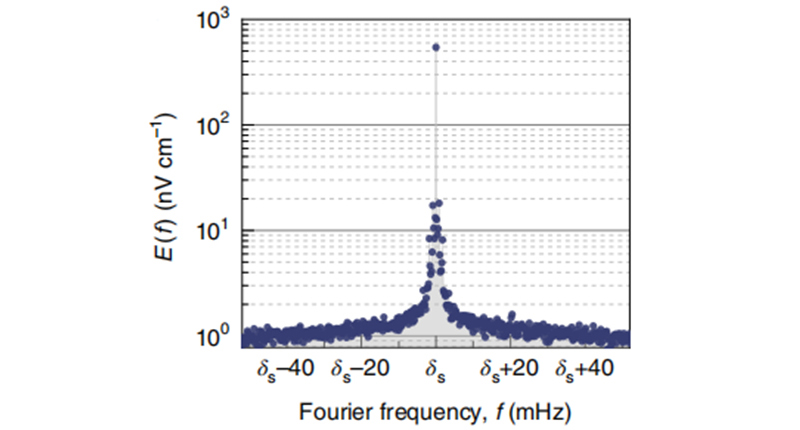
图9 微波电场在T=5000s时的典型单边傅里叶频谱

图7显示，原子超外差也实现了比所有其他原子传感器更高的性能，其微波场测量精度低于8μVcm^-1。最小不确定度在1s的测量时间内为10^-8Vcm^-1，基本上由基于EIT谱的光学测频精度决定。图7还比较了原子超外差法和标准天线法的测量结果。在177nVcm^-1≤E _S≤1.78mVcm^-1的范围内，它们不确定度均为约5%。可以认为，这种不确定性源于与设置微波发生器输出功率的天线方法有关的不确定性。原子超外差单次测量的相对统计不确定度随信号的减小而增大，但可以通过多次测量的平均值来减小。当E _S<177nVcm^-1或E _S>1.78mVcm^-1时，原子超外差的系统不确定性才变得显著，前者由于信号和噪声的非相干和，后者由于线性关系的分解。在极弱场范围的测量补充了对于强磁场的AT分裂测量，。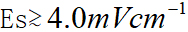

图10显示了原子超外差感知多普勒频移和识别目标运动的能力，在航空、气象和生物医学等领域具有重要作用。在实验中，发射的微波从一个周期性运动的物体反射出来，这个物体被原子超外差接收（连同发射的微波一起）产生P_out (t )，模拟多普勒雷达探测。相应的单边傅里叶振幅谱显示五个明显的峰值（如图10），中心峰值对应于发射频率。测得的多普勒频移δf =±4.4mHz，由此确定物体朝向（或远离）天线的径向速度，即ν=95μms^-1。两个侧峰距中心2δf 远，表明发生了多次反射。频率分辨率为0.2mHz，受快速傅里叶变换（FFT）的分辨率带宽（RBW）的限制。频率精度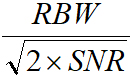，，对于数百nVcm^-1的磁场，达到亚μHz。当前原子超热的带宽超过100kHz，这使我们能够测量从几μms^-1到几kms^-1的速度，涵盖了从细胞迁移到火箭快速飞行的运动。

图10 原子超外差感知多普勒频移的单边傅里叶振幅谱

原子超外差分解微波相位的能力如图11所示。从P (t )中提取的相位Φ_out 和真实相位Φ_S 显示出良好的一致性。通过测量对应于跳跃输入相位Φ_S 的Φ_out ，可估计相位分辨率为0.8°，与理论一致。

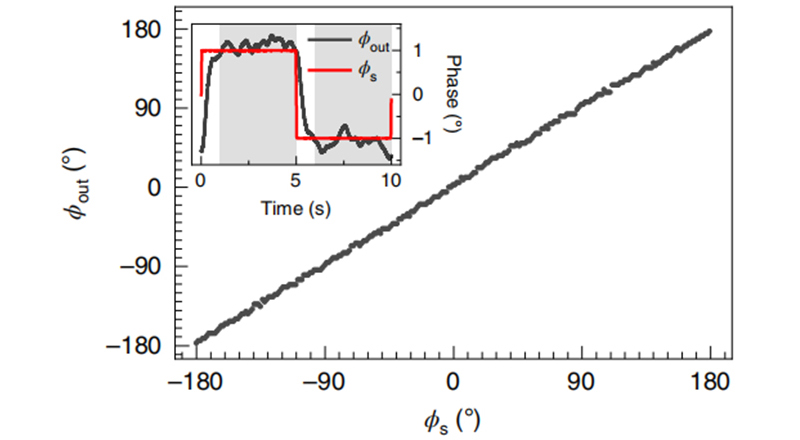
图11 Φ_out 和Φ_S 的关系曲线

2.4 应用前景

以上介绍了一种基于微波修饰里德堡光谱的新型微波传感技术，它可以同时实现超高灵敏度信号电场的SI可追踪测量以及相位和频率的检测。通过产生有利的缩放，该技术显著提高了当前实验工作的效率，以降低灵敏度增益的经典噪声，从而为实现量子投影噪声限制（QPNL）下的灵敏度开辟了一条可行的途径，这在当前的实验中是极具挑战性的。从目前的技术和非经典资源的组合中，可以预期灵敏度将会得到进一步提高。同样吸引人的是将里德堡原子超外差应用于超小场区可追踪微波电场标准的前景。该技术可推广应用于从射频区到远红外区的电磁辐射检测，并具有小型化的可行性。该研究在实现未来量子接收机的道路上迈出了一大步，例如在雷达或射电望远镜中，具有SI可追踪精度和超高灵敏度的优点；在太赫兹通信中，也可通过相位或频率调制恢复太赫兹载波中编码的信息。

三、微波场精密测量的总结与展望

3.1 横向趋势

由于历史发展原因，微波场精密测量技术早期的发展主要集中在美国、西欧等较发达地区，中国在该方面的研究起步较晚。但随着我国对量子研究的不断深入，中国科研团队在国内和国际上取得了一次又一次突破。山西大学贾锁堂、肖连团教授团队、南京航空航天大学潘时龙教授团队等的研究成果，都在国际上引起轰动。当前国内众多高校都在微波场精密测量方向投入甚多，中国在该方向的研究已呈现比肩甚至超越欧美的趋势。

3.2 技术更新

早期的微弱电磁场测量都是基于电子来进行的，但随着技术的不断进步，人们发现基于里德堡原子的微波精密测量具有更高的精度和灵敏度，便发展了原子微波电场计和原子微波磁场计两大分支。同时，基于光子的探测和成像技术也得到进一步发展和成熟。未来，极有可能有更具优势的新技术涌现，微波场精密测量将得到进一步发展。

3.3 纵向趋势

随着时间的推进，由于技术的更新，精密测量技术的精度在纳米级方向得到进一步的发展，精密测量分辨率不断提高，不确定度不断降低。里德堡原子微波电场计刚起步时，实现的微波电场测量灵敏度虽已可达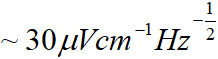，但最新技术已经达到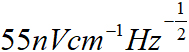。原子微波磁场计和微波光子雷达的灵敏度也同样在不断刷新。可以预见，未来精密测量技术将越来越精密化、精准化，人类对微观领域的度量将越来越得心应手。

3.4 应用前景及展望

目前，微波场精密测量方面的一些新技术尚处于孵化阶段，还未得到成熟应用。随着技术的进一步成熟和可靠性的不断提高，其在科研、军事、探测、医学、制造、通信等各个领域的应用必然会愈加广泛。

譬如，当前我国芯片发展的一大障碍便是芯片的微型化与电磁干扰间的矛盾，而使用微波场测量技术，就可精确探测出芯片整体和局部的电磁场走势，从而为解决方案的提出和实现提供了可能性。并且可以试想，运用该技术，可以精确看出芯片内部正在传输与变换的信号，若是芯片某一部分出现问题，就能轻而易举地检测出^[18-20]。

并且，该技术应用于生活，也将给人们带来极大便利。如在医学检测中运用精密测量，人体中各种生物信号的微弱变化都能被发现，从而许多疑难病症的诊断和治疗，甚至某一生命体征微小异常带来的潜在危害预见，都将得到实现。

综上所述，微波场精密测量技术发展前景广阔，在不远的将来必然会作为一项新兴技术造福社会。

参考文献：

1. BÖHI P, RIEDEL M, HÄNSCH T, et al. Imaging of microwave fields using ultra cold atoms[J]. Applied Physics Letter 2010; 97(5):051101.
2. HORSLEY A, TREUTLEIN P. Frequency-tunable microwave field detection in an atomic vapor cell[J]. Applied Physics Letter 2016; 108(21):211102.
3. AFFOLDERBACH C,DU G,BANDIT et al. Imaging microwave and DC magnetic fields in a vapor-cell Rb atomic clock[J]. IEEE Transaction on Instrument and Measurement 2015; 64(12):3629-3637.
4. HORSLEY A, DU G, PELLATON M, et al. Imaging of relaxation times and microwave field strength in a micro fabricated vapor cell[J]. Physical Review A 2013; 88(6):063407.
5. Dietsche EK, Larrouy A, Haroche S, Raimond JM, Brune M, Gleyzes S. High-sensitivity magnetometry with a single atom in a superposition of two circular Rydberg states[J]. Nature Physics 2019; 15(4):326-329.
6. 孙富宇. 原子微波测量技术[J]. 时间频率学报 2018; 41(3):171-178.
7. SEDLACEK J, SCHWETTMANN A, KÜBLER H et al. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances[J]. Nature Physics 2012; 8(11):819-824.
8. HOLLOWAY C, GORDONJ, SCHWARZKOPF A et al. Sub-wavelength imaging and field mapping via electromagnetically induced transparency and Autler-Townes splitting in Rydberg atoms[J]. Applied Physics Letter 2014; 104(24):244102.
9. GORDON J,HOLLOWAY C,SCHWARZKOPF A,et al. Millimeter wave detection via Autler-Townes splitting in rubidium Rydberg atoms[J]. Applied Physics Letter 2014; 105(2):024104.
10. ANDERSON D,MILLERS,RAITHEL G,et al. Optical measurements of strong microwave fields with Rydberg atoms in a vapor cell[J]. Physical Review Applied 2016; 5(3):034003.
11.ANDERSON D,RAITHEL G. Continuous-frequency measurements of high-intensity microwave electric fields with atomic vapor cells[J]. Applied Physics Letter 2017; 111(5):053504.
12. Jing M, Hu Y, Ma J, Zhang H, Zhang L, Xiao L, et al. Atomic superheterodyne receiver based on microwave-dressed Rydberg spectroscopy[J]. Nature Physics 2020; 16(9):911-915.
13. 史经展. 光子学辅助的微波相位噪声测量方法[R]. 2021.1.20.
14. 潘时龙, 张亚梅. 微波光子雷达及关键技术[J]. 科技导报 2017; 35(20):36-52.
15. Zhang F, Guo Q, Wang Z, et al. Photonics-based broadband radar for high- resolution and real- time inverse synthetic aperture imaging[J]. Optics Express 2017; 25(14): 16274-16281.
16. Fan, H. et al. Atom based RF electric field sensing[J]. Journal of Physics B 2015; 48(20).
17. Sedlacek, J. A. et al. Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances[J]. Nature Physics 2012; 8: 819-824.
18. Guo-Bin Chen, Bang-Xing Gu, Wen-Hao He, Zhi-Gang Guo, and Guan-Xiang Du，“Vectorial Near-Field Characterization of Microwave Device by Using Micro Diamond Based on Tapered Fiber [J]. IEEE Journal of Quantum Electronics 2020; 56, 7500106.
19. B. Yang, M. M. Dong, W. H. He, Y. Liu, C. M. Feng, Y. J. Wang, G. X. Du Using Diamond Quantum Magnetometer to Characterize Near Field Distribution of Patch Antenna [J]. IEEE trans. on Micr. Theo. and Tech. 2019; 67, 2451.
20. B. Yang, Y. Dong, Z. Z. Hu, G. Q. Liu, Y. J. Wang, G. X. Du. Non-Invasive Imaging Method of Microwave Near Field Based on Solid State Quantum Sensing. IEEE trans. on Micr. Theo. and Tech. 2018; 66, 2276.