数字调制系列：IQ调制及解调简述

前面在文章“数字调制系列：如何理解IQ？” 和“数字调制系列：IQ 基本理论”中介绍了IQ的概念、常用数字调制方式及映射星座图等内容，当完成数字比特流到IQ 坐标系的映射后，便可以得到数字I 和Q 信号，然后分别经过DAC 变换为模拟I 和Q 信号，最后经过IQ 调制器完成上变频，图1给出了数字调制的简要架构示意图。作为整个数字调制发射系统的关键部件，IQ 调制器完成了基带信号的频谱搬移，从而达到空口传输的条件。

什么是IQ 调制器？IQ 调制器如何工作？接收侧如何解调出IQ信号？本文将给出具体介绍。

图1. 数字调制发射系统架构示意图

1. 什么是IQ 调制器？

图2给出了IQ 调制器的简要架构示意图，通常包含四个端口：模拟I 输入端口，模拟Q 输入端口，LO (本振) 端口以及射频输出端口。有的IQ 调制器还支持差分模拟I/Q 输入，因此具有更多的端口。IQ 调制器包括两个对称的支路，每个支路包含一个Mixer (上变频)；两个Mixer 的LO 同源，但是要求正交，即存在90°相位差。

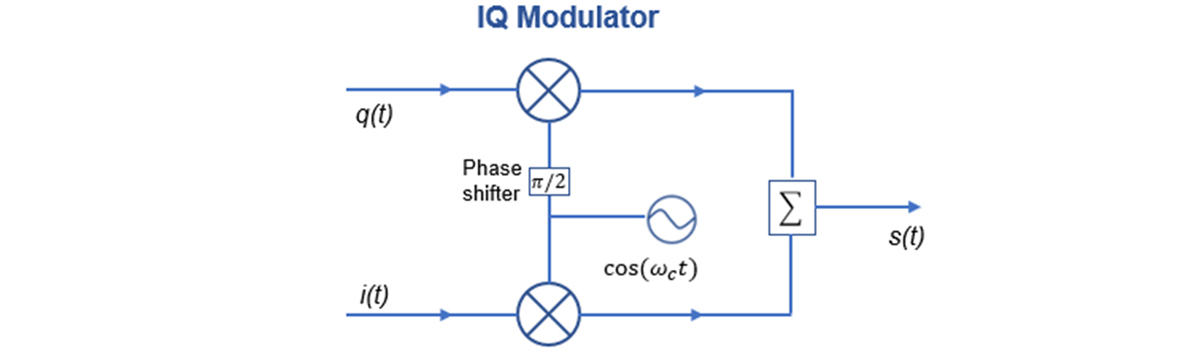
图2. IQ调制器架构示意图

IQ 调制器具有三个比较关键的性能指标：

(1) 整个带宽内的频率响应；

(2) 两个支路间的幅频响应对称性(IQ增益平衡)；

(3) 两路LO 信号的正交性。

这些指标的优劣将直接影响信号调制质量的好坏。IQ 调制器的频率响应包括幅频响应和相频响应，对于理想的线性时不变系统(LTI)，幅频响应是平坦的，相频响应是线性的，信号可以无失真的传输。因此，频响性能越好，调制质量越高，从系统的角度讲，BER 越低。

为什么要强调IQ 调制器两个支路间的幅频对称性呢？如果两个支路的频率响应不同，就会造成IQ 不平衡传输，当产生中心频率与IQ 调制器LO 频率不同的信号时，镜频分量抑制效果会变差。因此，需要控制IQ 调制器支路间的幅频特性差异。

类似地，两个Mixer 的LO 正交性也将会影响镜频抑制能力。如果完全正交，则不会对镜频抑制能力有影响。当偏离正交时，镜频分量会增强。

如果模拟IQ 调制器的特性不是很理想，势必会影响信号的调制质量。但是，可以通过源端预失真来补偿，从而改善信号质量，比如矢量信号源中允许调整I/Q Imbalance 及I/Q Quadrature 参数等。

2. 发射端调制器是如何实现IQ调制的？接收端解调器又是如何实现IQ解调的？

此处信号的调制与解调，仅限于模拟IQ 信号到RF，再从RF 信号解调出模拟IQ 信号。通过下面的介绍，除了调制与解调的过程，您还将会了解为什么基带I 和Q 信号的带宽经过IQ 调制器后会翻倍。

为了便于理解，首先介绍一下信号的单边带频谱与双边带频谱。这两种频谱都可以准确描述信号的频谱，但是出发点不同，应用场景也不同。   

任何一个周期信号，只要满足狄里赫利条件，均可以写为一组完备正交集函数的无穷级数。通常完备的正交集函数为三角函数，比如{cos(n Ωt )；sin(n Ωt )，n 为任意非负整数}；根据欧拉公式，三角函数与虚指数函数存在一定的关系，因此周期信号也可以写为虚指数函数的无穷级数。

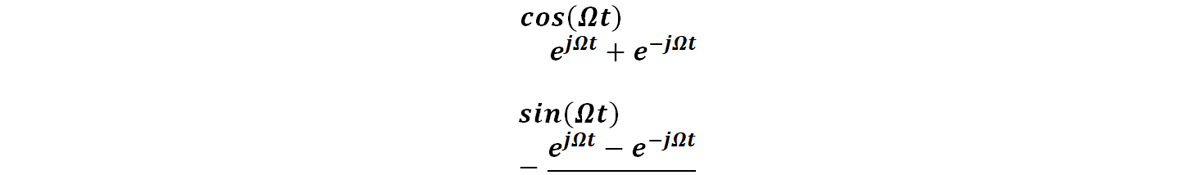
如果按照三角函数级数展开，则对应的频谱为单边带频谱，如果按照虚指数函数级数展开，则对应的频谱是关于零频左右对称的频谱，此时称为双边带频谱。由于运算更加方便，双边带频谱应用更加广泛。

对于调制应用而言，涉及到频谱的搬移，因此采用双边带频谱更加方便。下文所涉及的频谱，均指双边带频谱。双边带频谱包括负频率成分，没有具体物理意义，但是从数学角度讲，这些又是构成傅里叶变换的必不可少的组成部分。

图2所示的IQ 调制器，在上变频的过程中，两个Mixer 实际上起到乘法器的作用，即i(t) 与cos(ω_ct )相乘，q(t) 与sin(ω_ct) 相乘，最后合为一路输出。

假设I(ω) 和Q(ω) 分别为i(t) 和q(t) 的傅里叶变换，而三角函数的傅里叶变换为

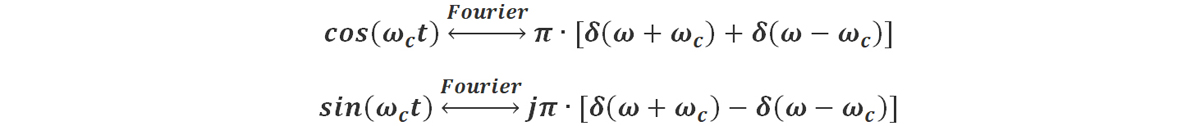
根据频域卷积定理可得：

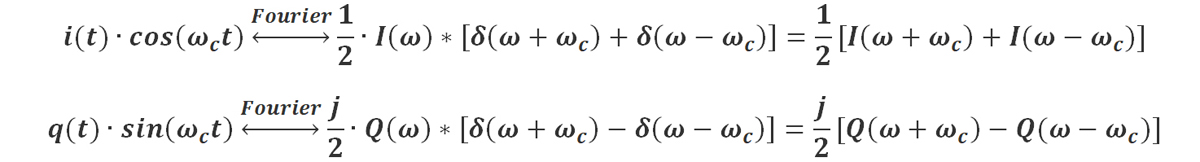
由此可见，i(t) 和q(t) 经过混频器后，从傅里叶的角度看，其双边带频谱发生了搬移，中心频率由DC 搬移至ω_c。傅里叶变换的产物中还包含(-ω_c)频率成分，如前所述，负频率不具有实际物理意义，但是作为傅里叶变换的重要组成部分，构成了整个变换的数学完整性。

虚数 j 的存在表明，两部分信号之间的载波存在90°相差，二者保持正交。

以上数学推导也可以由图解完成，图3给出了正、余弦函数的傅里叶变换示意图，模拟IQ 信号经过调制器后，频谱变换示意图如图4所示。

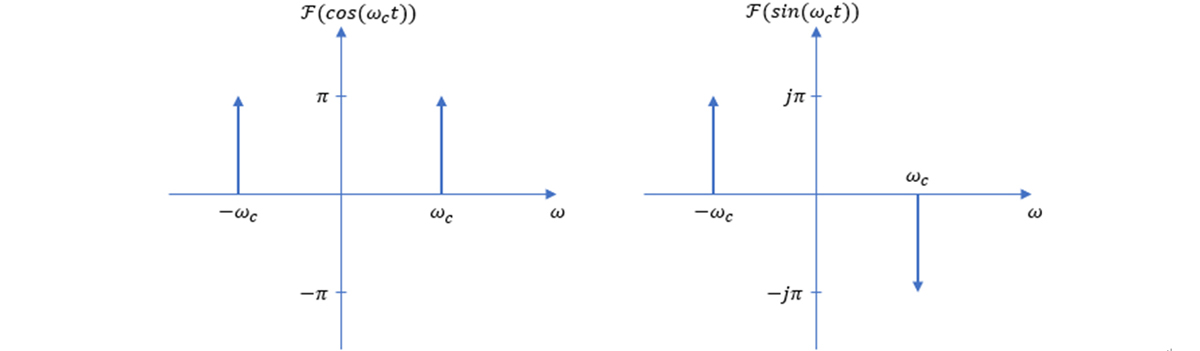
图3. 正、余弦三角函数的傅里叶变换

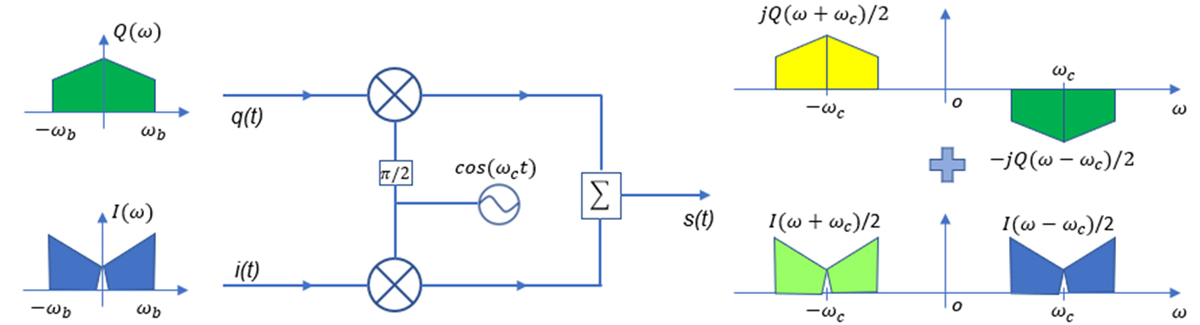
图4. IQ调制频谱变换示意图

因采用双边带频谱描述信号，i(t) 和q(t) 实际带宽为双边带频谱带宽的一半，由上述推导可知，当经过IQ调制器上变频之后，整个双边带频谱搬移至射频，故输出的信号s(t) 的带宽相对于基带模拟IQ信号的带宽翻倍了。

在接收侧，射频调制信号可经过模拟IQ解调器解调，经过低通滤波器之后分别得到模拟I 和Q 信号。数学推导与IQ调制类似，此处不再赘述。图5给出了IQ解调器的整个图解过程，非常清晰地表明了如何由射频信号得到模拟IQ信号。

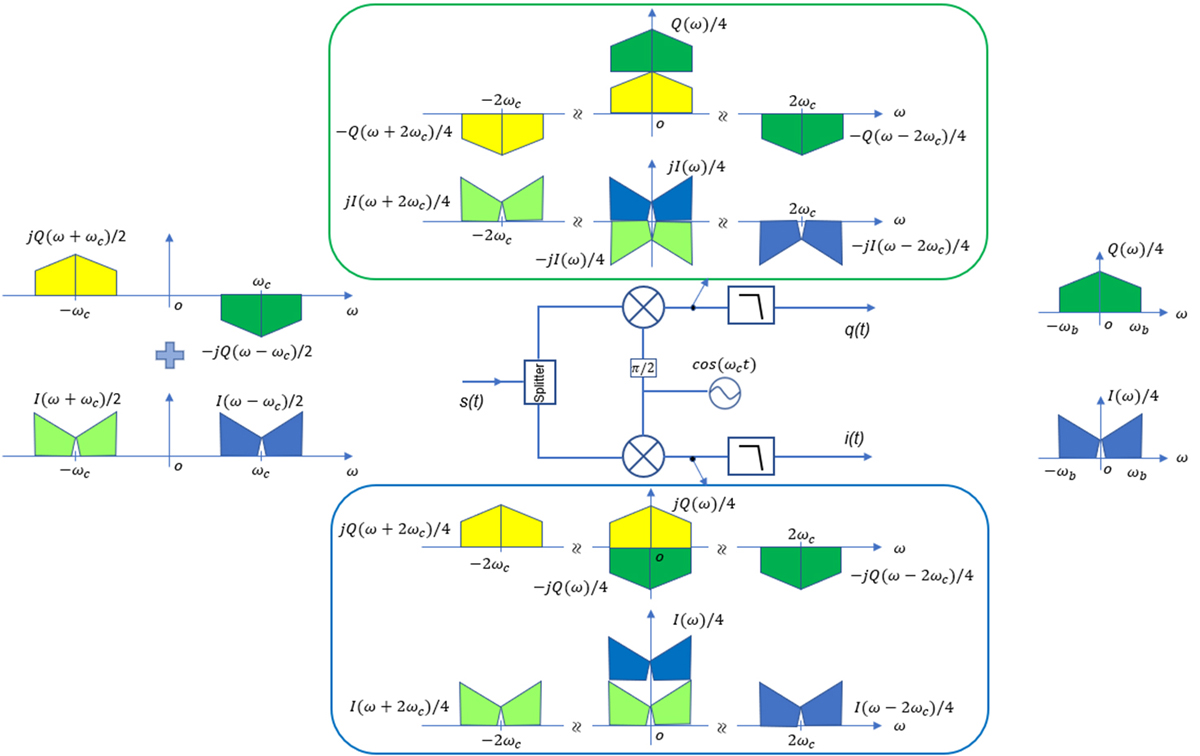
图5. IQ解调频谱变换示意图

3. IQ调制与解调的实现方法有哪些？

前面介绍调制及解调过程时，默认是按照模拟IQ调制/解调器介绍的。现实中绝大多数数字调制发射系统均是采用了模拟IQ 调制器，从测试设备的角度讲，矢量信号源也是采用了模拟IQ 调制器的架构。尽管如此，IQ 调制功能也是可以通过数字的方式实现的，称为数字IQ调制器，在数字侧完成符号映射及IQ 调制，从而得到具有载波的波形，最后经过DAC 直接播放出来。任意波信号发生器(AWG) 产生数字调制信号就是采用这种方式，但是DAC的时钟频率决定了能够输出的最高信号频率。

类似地，模拟IQ 解调器的功能也可以由数字方式实现，称为数字下变频。而且相对于模拟解调器而言，数字下变频应用更加广泛。其基本思路为：射频信号经过下变频至IF 频段，然后经过ADC 直接离散化，对离散的数据作数字下变频便可以得到数字IQ 信号，最后对IQ 数据进一步分析。现在的矢量信号分析仪基本都是采用这个架构，有的矢量信号分析采用示波器及分析软件的方案，也是应用了数字下变频技术，如图6所示，示波器的最大优势就是支持更高带宽信号的分析，这是矢量信号分析仪所远远不及的。

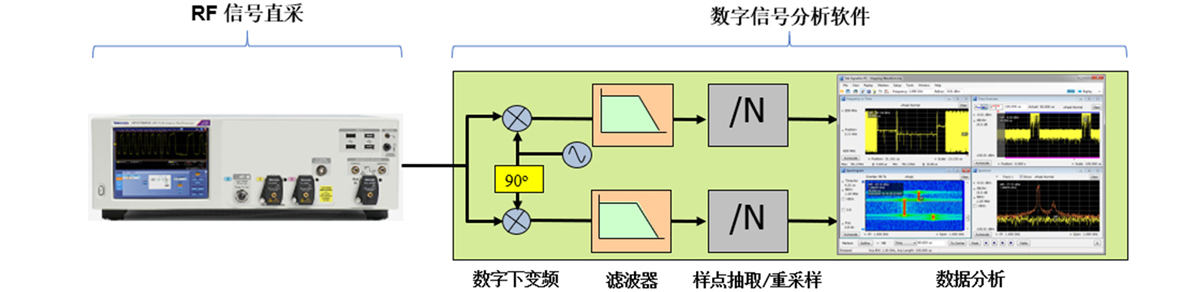
图6. 矢量信号分析架构示意图

小结

之前的文章介绍了关于IQ 和数字调制方式的基本概念，本文继续深入剖析数字调制，重点介绍了数字调制过程中的关键部件——IQ 调制器及其特性，并从解析和图解两个方面详细描述了IQ 调制与解调的过程，以便于理解数字调制。对于目前常用的IQ 调制与解调的实现方式，文末也给出了相应的说明。