射频电缆的无源互调测试

模型的右边是端口2，该端口也会产生一个不希望出现的小互调能量，以IM2表示。所有用于端口1的假设同样适用于端口2。通观完整的集成电缆无源互调的测量模型，以下几条值得关注：

每个测试端口都有与其相关的4个互调响应。其中两个是接头末端产生的，另两个是互调分析仪自身产物。

电缆b端的互调（IMb）和端口2的互调（IM2）会通过电缆反向传输，从而产生的反射互调响应可以在端口1处测量。

电缆a端的互调（IMa）和端口1的互调（IM1）会通过电缆进行传输，从而产生的通过互调响应可以在端口2处测量。

通过这个模型，集成电缆的互调值就可以被确定了。

四、使用模型预计互调特性

虽然预计一个给定的射频器件的互调绝对值是非常困难的，但是单个互调源之间的相互作用在图2的模型中可以很容易地被表现出来。

首先，我们已经知道了每一个互调源的三阶互调公式。以端口1和电缆a端的响应开始，互调响应为：

三阶互调的频率为：
w₃ ≡2ω₂ −ω₁

其中
t：时间
IM1：端口1的三阶互调响应
IMa：电缆a端的三阶互调响应
σ₁：端口1的互调系数，即端口1(=10^[dBc/20.])的dBc响应的简单数字转化
σ_a：端口a的互调系数，即端口a(=10^[dBc/20.])的dBc响应的简单数字转化
ω_{1, 2, 3}：分别为载波1，载波2和产生的三阶互调响应的频率弧度

电缆b端和端口2的互调响应相对稍微复杂。两个载波产生的互调响应可以通过电缆传输函数H(w)表示。为了简化公式，和消除非线性功率对互调产物及其载波的影响，假设电缆是无损耗的。在公式中，这个假设表示为：
|H(w) |= 1

当最终结果出来时，这个假设对于模型精确度的影响是非常显著的。

即使假设电缆是无损耗的，电缆产生的群时延还是被包含在模型中的，具体如下式：

其中：
k：与频率有关的通过电缆(2p/l)的电磁波数
v：同轴电缆的传输速率
L：电缆的长度

电缆b端和端口2的互调响应表示为：

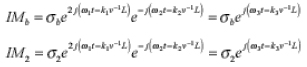
当公式中IMa、IM1、IMb、和IM2已知，落在端口2上，总的通过（前向）互调表达式为：

上式表示同时落在互调测试设备端口2上的四个互调响应，不依赖于互调频率。假设单独的互调源是不依赖于频率的，且电缆的损耗是一个常数，那么整条集成电缆的通过互调响应将不依赖于频率。

我们可以采用相似的过程来描述反射互调响应。反射互调响应可以由下式来给出：
Reflected IM at Port ( 1) = IM_a + IM₁ + H(w)∗(IM_b + IM₂ )

简化为：

上式表示端口1中的反射互调响应是端口1和电缆b端响应的合成，加上由于电缆b端和端口2的互调响应的合成造成的移相响应。由于存在一个不同相位的互调源的合成向量，所以，我们认为反射互调响应是一个与电缆的频率和电长度有关的函数。

五、集成电缆互调响应的测量

为了验证该模型，我们使用SI-1900A型无源互调失真分析仪来测量无线通信应用中一种典型的集成跳线。该集成跳线长1.5米，厂商标注的速率因子为82%，两端分别安装有一个DIN-M型接头。载波功率设置为20W/路。分析仪的自适应逻辑电路确保了测试过程中，载波的功率变化不超过0.2dB。分析仪的底噪不超过-140dBm，即当施加一个+43dBm的载波功率时，分析仪的互调底噪不超过-163dBc。

图3显示了反射和通过互调响应的测量结果曲线，以及相应的预测曲线。电缆每个端口上的互调响应值，是通过假设前向互调响应是由两个分别在电缆两端的等幅互调源之和组成的。反射互调响应值仅由该模型来决定，且不用调节使之与测得的数据相匹配。