低频谐波失真度仪设计

      目前，测量失真度的仪器根据测量原理大致可分为二大类：基波剔除法和频谱分析法。一般模拟式的失真度测量仪都采用基波剔除，这种仪器测量的误差较大;而频谱分析法，则是利用频率分析仪测量各次谐波的含量并计算出波形失真度的方法。它可分析测量出被测信号中的1～10次谐波分量。采用该方法较好地解决了超低频率失真度的测量，缺点是仪器结构复杂，价格较贵，操作繁琐。

　　1 测量原理

　　一个失真的周期振荡信号电压，除有基波电压分量外，还有各次谐波分量存在，把周期失真的正弦信号展开成傅立叶级数，可表示为：

　　其中，f(t)是一含有谐波失真的正弦波，A0＝上式中，A0/2为正弦波中直流分量，An为第n次谐波的振幅，n为失真正弦波中所含最高谐波次数，ω0为标准正弦波的角频率，φn为第n次谐波相对于基波的初相角。

　　一般地，正弦波的失真是用失真度，即所有谐波能量之和与基波能量之比的平方根来表示的：

        数为n次的失真度，只要求出各次谐波的幅值，就可计算出信号的失真度。在实际测量中由于实现困难，模拟失真度仪测量所测出的数值是各谐波电压有效值和总的电压有效值之比，

　　即

        模拟失真度仪的原理框图如图1所示。

　　被测信号经过放大器后，首先直接进入电子电压表，测出其总电压的有效值，并调至100。然后，信号通过滤波器，滤去基波成分，再次进入电子电压表，测出剔去基波后电压的有效值，此时指示即为失真度。显然，它只是失真度的近似值，必要时必须进行补偿。 　　基于FFT的失真度仪，采用频域分析方法，通过计算傅立叶系数，C1、C2…Cn，最后得到失真度大小。

　　由失真度定义得：

　　基本方法就是通过傅立叶变换(FFT)，产生出信号的频谱图，根据频谱含量的大小Cn，计算出失真度。此类分析需要频谱分析仪和同步示波器。本文提出一种由虚拟仪器实现的、基于FFT的失真度测量，该失真度测量仪硬件原理如图2所示。

　　2 虚拟实现

　　(1) 虚拟仪器建立在计算机平台上。计算机通过数字采集卡采集被测信号，经A/D转换后读入计算机，由计算机对采集的信号进行傅立叶变换(FFT)，形成被测信号的二维幅度-频率数组。计算机显示出信号的幅度-频率特性曲线，同时，对数组计算得到基波系数和各次谐波系数，最后，由基波和各次谐波系数计算出失真度。

　　(2) 开发平台使用美国国家仪器公司(National instruments corporation)的Labview,硬件为兼容586计算机及NI公司的数据接口卡PCI-1200。

　　(3) 软件编制采用Labview提供的图形编程语言。完成被测信号的采集和波形显示 、信号的傅立叶变换(FFT)、信号的幅频曲线显示、信号的傅立叶基数的系数计算及信号的失真度的计算和显示。

　　3 测试结果

　　采用该虚拟失真度测试仪分别对两类信号进行了测试比较。其一是计算机产生的数字合成信号;其二是信号发生器产生的正弦波信号。

　　3.1 对数字合成信号的测试 　

    　(1) 计算机产生合成失真的正弦波f(t)=5sin3.14t+0.3sin(7%26;#215;3.14t)。用虚拟失真度仪测量结果如图所示。 　

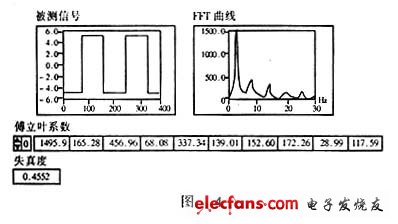
        (2) 数据比较：对于正弦信号f(t)=5sin3.14t+0.3sin(7%26;#215;3.14t)，其失真度的理论值为： =0.06，与测试值相同。

        3.2 对实际信号的测试 　　

         信号发生器采用JRC811(景德镇无线电厂生产)，产生占空比为50%、频率为3Hz、幅度为1的方波信号。由虚拟失真度仪分别测试并与理论值进行比较。

　　3.3 虚拟失真度仪与通用失真度仪的比较 　　

         由信号发生器(JRC811)产生约100Hz正弦信号，用虚拟失真度仪和北京无线电仪器二厂生产的SB失真度仪分别进行测量，其结果如下：

　　SB测量结果约 =0.01，与虚拟仪器测量结果相同。

　　3.4 误差分析 　　

         采用本方法的失真度测量的误差主要包括A/D测量误差、FFT计算时的舍入误差和周期采样FFT分析泄漏引入的。其中FFT分析泄漏引入的误差是最主要的因素。

　　4 结 论 　　

        (1) 具有较高的精度。利用基于FFT失真度分析程序测量失真度具有较高的精度，完全满足一般实验中波形失真度的测量要求。 　　

        (2) 程序采用了FFT分析算法，人机界面良好。　　　　

        (3) 用户只要用一台微机和数据采集卡，不再需要其它硬件电路设计，即可完成失真度测量，省去大笔购置失真度测试仪的费用。 　　

        (4) 易于移值，在其它数字测量仪器上，不用增加其它硬件，通过软件的修改即可增加此功能。