基于软件无线电的FM解调算法

摘要：软件无线电的基本思想是将宽带A／D及D／A尽可能靠近天线，将无线电台的各种功能在一个开放性、模块化的通用硬件平台上尽可能多的用软件来实现。软件无线电已成为移动通信中的关键技术之一。文中基于软件无线电采用软件实现通用硬件调制的目的，通过基带信号处理算法，结合软件无线电接收机中的相关理论对其中的调制方式识别和解调算法进行了仿真，说明了各个解调模块的功能，而且也验证了系统的科学性和可实现性。

关键词：软件无线电；调制解调模型；算法；载波同步；定时同步

无线通信系统有许多种的调制方式，这些调制方式由于其自身特点而也适用于各种不同场合。由于其通讯模式不兼容，所以满足不了不同通讯模式之间的兼容要求。而且，因为不同频段的电台也只能满足某些特定的要求，无法满足各种各样的军事需求。

软件无线电这一新概念一经提出，就得到了全世界移动通信领域的广泛关注。根据软件无线电拥有的灵活型、开放型等特点，使其不仅在军事民用移动通信中得了应用，而且会在其他如电子战、雷达、信息花家电等领域得到更广泛的应用。

1 软件无线电简介

软件无线电的基本原理是在一个通用划、标准化、模块化的硬件平台上，用软件编程来完成无线电台的各种功能，不同于创痛的基于硬件、面向用途的电台设计模式。要用软件来实现功能实现就需要求减少功能单调、灵活型差的硬件电路不分。尤其是减少模拟处理部分，让数字化处理器(A／D和D／A变换)尽可能靠近发射端。软件无线电的核心是整体结构的开放型和全面可编程型，即可以利用软件的更新实现硬件的协调，从而实现新的功能。一般采用总线结构，因为具有标准的、高性能的开放式，方便对硬件模块的升级和扩展。

相应的软件无线电的结构如图1所示。

图1 软件无线电组成结构图

2 研究发展现状

目前，软件无线电在军事通信及移动通信领域研究非常活跃。软件无线电在3G通信系统中也有许多应用实例。国内软件无线电方面的研究尚处于起步阶段，目前只有几家单位进行这方面的研究，而且相互之间很少交流。要在这方面取得突破性的进展尚需一段时间。

3 软件无线电解调模型

从理论上来说，各种通信信号都可以用正交调制的方法加以实现，如图2所示。

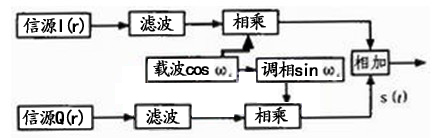
图2 正交调制实现框图

根据图2，可以写出它的时域表达式：
调制信号S(t)为
S(t)=I(t)cos(ωct)+Q(t)cos(ωct)(1)
ωc=2πfc (2)
ωc为采样频率的角频率。在对调制信号和载波频率进行数字化时，其采样频率可能不一样。这里多相滤波器的主要作用就是用来提高数据源的采样速率，使得调制信号的采样速率和载波的采样速率一致。

尽管调制样式多种多样，但实质上调制不外乎用调制信号去控制载波的某一个(或几个)参数，使这个参数按照调制信号的规律而变化的过程。载波可以是正弦波或脉冲序列，以正弦型信号作为载波的调制叫做连续波调制。

对于连续波调制，已调信号的数字表达式为：
S(n)=A(n)cos[ω(n)n+θ(n)](3)

调制信号可以分别“寄生”在已调信号的振幅、频率和相位θ(n)中，相应的调制就是调幅、调频及调相这三大类熟知的调制方式。由于频率与相位有着一定的关系，为便于分析，可将上式改写为：

这就是利用XQ、XI直接计算f(n)近似公式。这种方法只有乘法和减法运算，计算比较简便。最后得到的软件无线电数字正交解调的通用模型。

4 仿真模型

4．1 解调信号的仿真

从理论上说，各种通信信号都可以用正交调制的方法加以实现，正交调制的模型如图3所示。在本例中，首先产生两列二进制的0、1序列I、Q，经过差分编码后，用两列正交载波信号对其进行调制，调制后的信号相加即可得到FM信号。调制后得到的FM信号如图3所示，图中横坐标为时间秒。在这里为了与上节相对应，我们所采用的仿真信号参数与之基本相同，载波频率为20 kHz，采样频率为160 kHz。

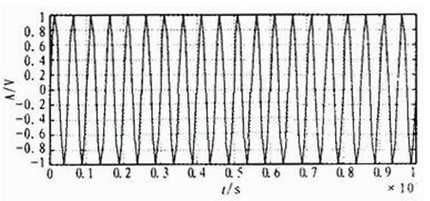
图3 FM信号

全数字FM解调器的核心问题在于对载波和定时的同步，其性能的好坏将直接对通信质量产生影响，因此将主要针对这两个同步来进行仿真。在本解调方案中采用数字相干解调的方式，这就要求接收方必须从接收信号中恢复出发射端载波信号，使双方载波的频率、相位一致。

FM调制信号是抑制载波的信号，无法用常规锁相环或窄带滤波器直接提取参考载波，其载波相位变化只能取有限的几个离散值，这就隐含了参考载波的相位信息。所以可以通过非线性处理，消除信号中的调制信息，产生与原载波相位有一定关系的分量，然后再提纯该信号，恢复己被抑制的载波信号，进而完成信号的相干解调。在这里采用基于判决的数字COSTAS锁相环来提出相干载波。COSTAS环的框图如图4所示。下面对照图4分析一下COSTAS载波同步环的工作原理。

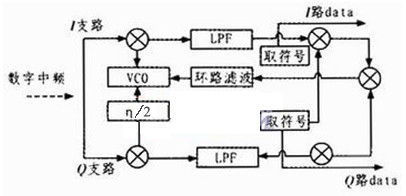
图4 科斯塔斯换的框图

如果不考虑噪声的影响，输入的数字化后FM信号可以表示为：
SFM=a(k)cosωck-b(k)sinωck  (12)

其中，ωc载波频率，a(k)、b(k)为发送的码元信号。假设数控振荡器产生的相干载波为：cos(ωck+△φ)，△φ调制载波与相干载波的相位差，经过相干解调输出的信号为：
I(k)=a(k)cos△φ+b(k)sin△φ  (13)
Q(k)=b(k)cos△φ-a(k)sin△φ  (14)

通过式13和式14可以看出I(k)、Q(k)两路数字基带信号中含有相位误差信息，那么科斯塔斯环的鉴相器得到的相位误差e(k)为：
e(k)=I(k)sign(Q(k))-Q(k)sign(I(k)) (15)

在科斯塔斯环的设计中，采用FIR低通滤波器作为匹配滤波器，通带截止频率为10 kHz，阻带起始频率为20 kHz。环路滤波器采用三阶切比雪夫低通滤波器，阻带起始频率为10 kHz。仿真后，鉴相误差和恢复的载波信号如图5所示。

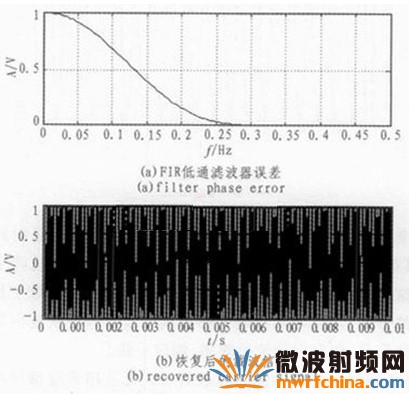
图5 滤波器的误差和恢复后的载波信号

从图5中可以看到，在0．4 s左右载波同步误差趋近于零，也就是说此时载波已经获得了同步，如果码元周期为0．1 s，那么经过4个码元周期就可以完成载波同步。

4．2 定时同步

数字通信系统是一个同步通信系统，应使收发两端信息码流速率和相位保持同步关系，因而需要同步信号来保证系统中传输的信息码流有同样的速率。当系统达到了准确定时后，将能够在接收信号的波形峰值点对其进行采样，使接收端有最大的接收信噪比。

信号经过匹配滤波后，输出数字基带信号，通过一个定时检测电路获取定时误差信息e(k)，通过环路滤波器和控制器反馈给内插模块，这就相当于在时域上再次采样，以得到正确的同步信号。

定时同步的首要问题在于定时误差的提取，在此Gardner算法使用的要更为广泛一些。它对每个信号波形需要两个采样值，而且对载波偏差不敏感，于是我们可以在定时恢复后再去纠正载波偏差，使这一任务得到了简化。Gardner算法求取定时误差为：en=(yn-yn-2)·yn-1，其中yn-1与yn相差半个信号波形周期。

采用Gardner算法进行仿真，输入信号的相位估值如图6所示。

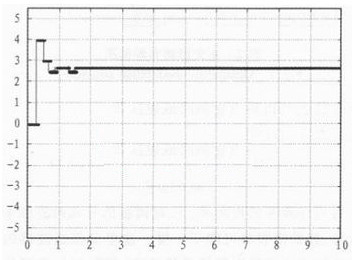
图6 输入信号的相位估值

经过定时同步后的输出信号就是经过相位校正后的输入信号，也就是说上图的I路和Q路信号就是的XI、XQ的值，根据前面介绍的解调算法就可以得到一组码元序列。为了避免相干解调时存在的相位模糊问题，我们在发送端对信号进行了差分编码，所以在接收端，只要进行差分译码就可以恢复出原始的传输信号。

5 结论

文中对软件无线电的结构和目前的关键技术做了一个概括性的介绍，并且对基带信号的处理算法进行了详细的讨论。在对基于决策理论的信号调制样式自动识别的算法进行仿真，该仿真过程不但说明了各个解调模块的功能，而且也验证了系统的科学性和可实现性。最后对一些能够影响接收机误码率的误差源进行了建模，通过仿真重点考察了载波同步和定时同步与接收机误比特率的关系，得到了静态相位误差、符号同步误差以及信噪比对误比特率的影响。

作者：杨明极，马琳