射频毫米波芯片设计11:基于奇偶模法分析设计射频微波Wilkinson功分器

《射频微波芯片设计》专栏适用于具备一定微波基础知识的高校学生、在职射频工程师、高校研究所研究人员，通过本系列文章掌握射频到毫米波的芯片设计流程，设计方法，设计要点以及最新的射频/毫米波前端芯片工程实现技术。

本文共计3部分

（全文阅读大概需8分钟，希望对您开卷有益）

1.前    言——讨论为啥要学奇偶模分析功分器

2.答    疑——对上一期《MOS管…》的疑问解答

3.浅    析——采用奇偶模对Wilkinson功分器分析

——————————————————

前言

​可能看到本期的标题大家就会想说，抛砖老师这功分器有啥好讲的嘛，不就是两根线条条+串一个小电阻就完事，还没我晚上去吃夜宵撸的串的花样多，这难道还能讲出一朵花来？而且我看好多公众号已经讲过了啊，抛砖老师你再不讲讲高端点的芯片设计，我可要取关报警了！

​且慢，其实，，，这个功分器呢，和我们之前讲到的滤波器，耦合器，天线（更多内容可以点击上方的文集列表去查看）一样，也是我们射频无源电路中的一个狠角色，在我们的射频电路中可有着不低的地位，比如说在相控阵系统中多通道是不是需要咱门的功分器出马，平衡式放大器是不是得他来做压舱石，还有混频器里的本振链路信号均分等等都有着她的倩影：

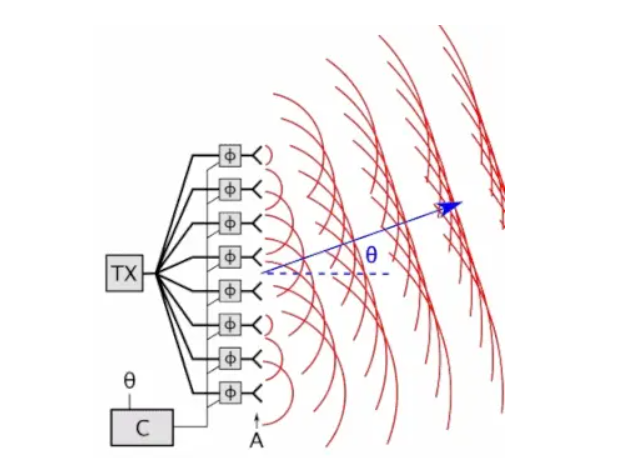
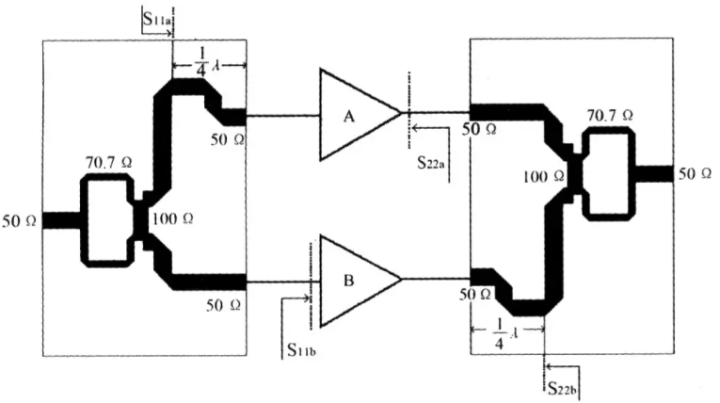
等等，，，我说抛砖老师，请不要转换概念，我说的是这玩意挺简单的，没说他不重要，这么简单的，是不是就没有必要讲了?

这。。。

那行，我先问大家3个关于Wilkinson功分器的问题，如果大家能1分钟之内快速回答出来，那么也就没有必要再浪费几分钟时间看后面的内容了：

1. Wilkinson功分器的隔离电阻是100欧姆，那为啥不是150，250？

2. Wilkinson功分器中的1/4波长线的阻抗，为什么是根号2倍特征值抗？

3. Wilkinson功分器的S参数矩阵是啥？

好了，大家先思考思考，如果心里有这三连的答案了，就大可跳过此篇文章，如果还是那种似是而非，说不出个所以然来的话，那我们可以接着往下看。

答疑

在采用奇偶模分析法去分析Wilkinson功分器之前，我们先对上一期《MOS管基础与特性…》里面的一个小问题进行答疑，这里主要分两点：1.对网友的质疑提出回复；2.对上期我们出的考题给予回应。

1.对网友的质疑的回复

​首先非常感谢该网友提出质疑，因为只有不断交流，很多知识才可以内化成自己的东西，就比如今天我们敞开心扉聊一聊这个P/N MOS的符号问题，如果这个网友看到了今天这篇文章，我相信他对这个知识点可以记忆深刻，以后在遇到类似的问题就会一点就通，因此鼓励大家多多提出自己的想法，多多交流，也可进群去和里面个个是人才说话有好听的老哥们侃大山，聊技术、职业规划、行业八卦等等。 好了，闲话我们少扯，我们先把视线拉回上一期3）中的符号表达式：

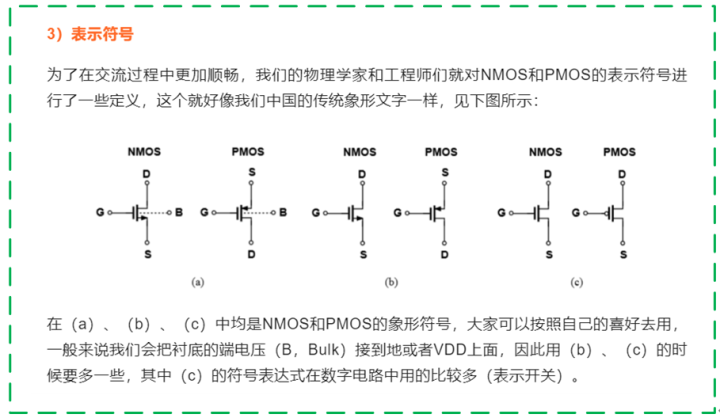
​矛盾点在于：在上一期，我们说到了（a）、（b）两种表达方式的N管符号箭头朝外，P管反之；但是网友提到的是，N管应该朝内，P管反之。 那到底抛砖老师错了，还是网友对了？这，其实两者都没毛病，但是呢，且看上期提到的反相器的原理图和版图：

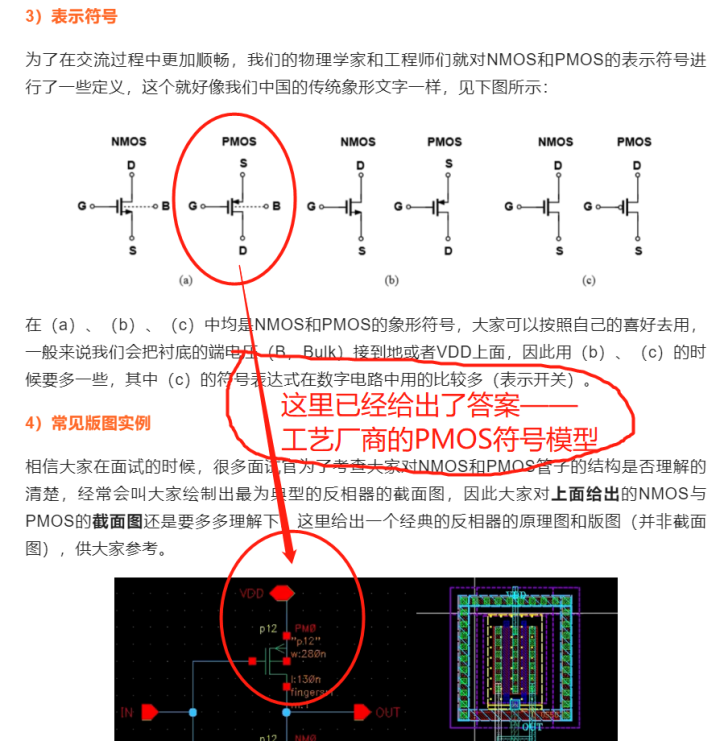
​根据观察，我们不难发现在现代工艺厂商，NMOS的箭头都是朝外，可是，此时又有网友说了，抛砖老师，我从小接受的教育不允许我撒谎，我以前学模电的时候，老师说NMOS符号箭头是朝内的，其实您说的对，之前的教材好多都是如此：

​那么之所以有这个矛盾，个人理解是在于看我们把箭头看成什么了，之前真空管过渡到固态电路的时候，我们往往还在聊载流子的走向，如果是NMOS管，那么我们源端（S）是给沟道提供载流子的，那么作为载流子的电子是朝着里面沟道流向的，换句话说，虽然电子是朝里但电流其实是朝外的，所以看似不同的表达，实则殊途同归。 上面的NMOS、PMOS的符号指向问题就讲到这里了，大家多活学活用，灵活处理各类小细节，比如再举一个关于课本和实际现实的非线性的例子： 上学的时候，我们一定接受过这样的观点，当我们把放大管的输出信号进行泰勒级数展开，得到如下公式，信号的二阶、三阶等高阶项就是非线性的（我们之前在《1.3万字详解射频基础...》中也是如此聊的），从数学层面来看，这没毛病吧！A(t)=a1x(t)是线性函数，多了几个高阶项，自然就是非线性的了，这应该没有什么好说的。

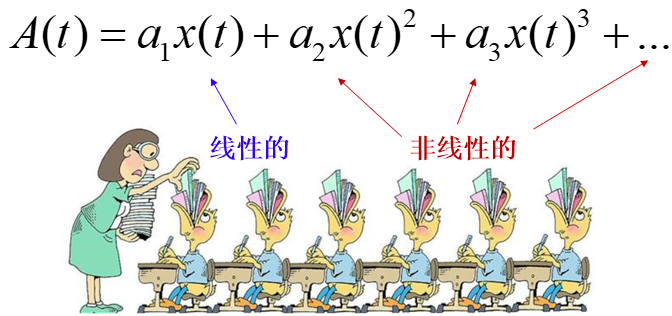
​但是，我们仔细想想，为什么呢，为什么要泰勒展开，背后又是什么物理原因导致的呢？这个时候，可能为了应付考试催眠自己，或许就会想 “泰勒说的嘛，工作在大信号下，MOS还想要线性度，不能，绝对不可能，非线性我泰勒吃定了，耶稣也保不住！”

​为了让大家更好地理解背后物理逻辑，我这里再给大家一个小小的提示，正如上一期我们提到的《MOS管的原理和工作特性》，我们的MOS管处于饱和区时：

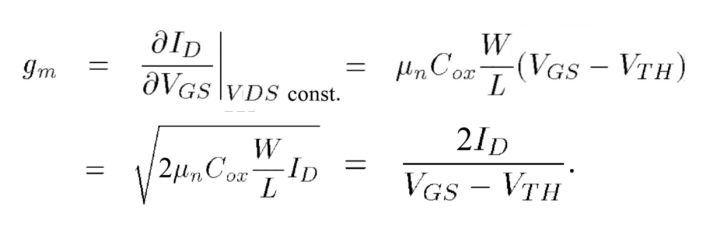
​在座的90%以上个个都是电子行业里说话又好听的人才，都说内行看门道，那我们不难发现上面的公式中，管子的放大能力与输入信号的大小有一定的关系，即gm是一个在特定条件下，与Vin正相关的函数，也就是说原来我们假定的线性放大A(t)=a1x(t)中的a1为一个常数不在成立，原来等式中的a1其本身就是一个关于x(t)的函数，这就会导致直线变成了其他曲线而非直线，也就是成了非线性。当然，这个肯定是有物理学家搞了一套理论的，比如“饱和萨式方程”等等。 好了还有很多电路小细节这里就不一一举例了，有兴趣的话后面有时间和篇幅了再来聊聊。这期继续给大家一个小思考题，上一期我们3）符号的表达里面的PMOS的源极（S极）为什么要标识在下面蓝色框框的位置？？？

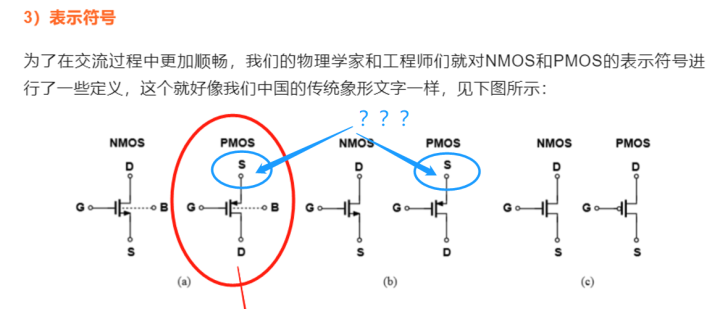
2.上期内容提出的小问题的解答

在上一期，我们提出了这样一个简单的问题，不知道大家有没有答案了呢？

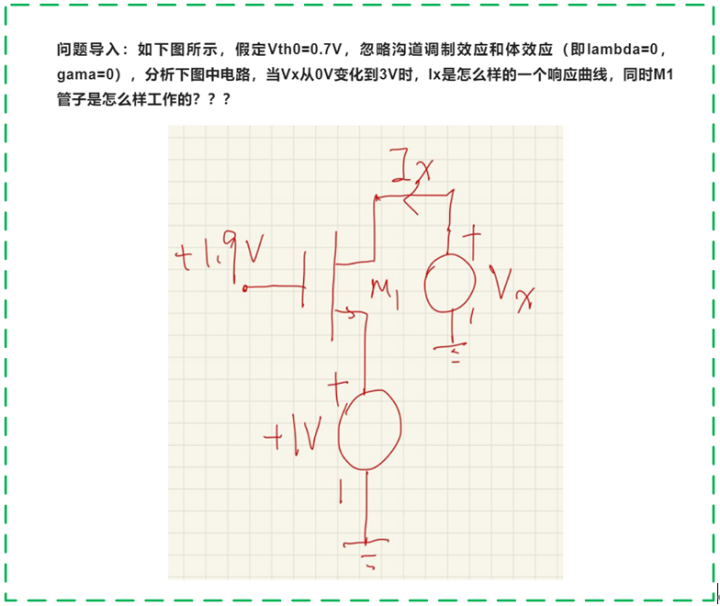
——RFIC抛砖·答案解析——

第一种情况：当Vx的电压为0~1V时，此时的D/S反向，即Ix的电流流向为负数（箭头反方向），此时M1处于线性区；

第二种情况：当Vx的电压为1~1.2V时，此时的D/S再次互换，即Ix的电流流向为正数（箭头方向），此时M1处于线性区；

第三种情况：当Vx的电压为1.2~3V时，此时M1处于饱和区；

具体解答过程如下所示

奇偶模法分析功分器

就如我们第2期《芯片滤波器设计..》谈到的耦合矩阵法去设计滤波器、第7期《低噪声芯片设计..》谈到的最小噪声匹配法以及噪声消除法去设计低噪放一样，每一个射频微波器件设计都会有一些自身比较有特殊的分析方法去进行设计。说到奇偶模分析法，这或许是射频微波人应该、也是尽可能需要掌握的分析方法之一吧，要不然咱可真就成软件的优化大师奴隶咯，即便工作多年，依旧会时不时陷入精神内耗。。。

那么，为什么要用奇偶模法来分析功分器呢？又是如何来利用奇偶模分析功分器？

为了解答这个问题，我们先把视线调整回Wilkinson功分器的基本结构中来，如下图所示，Wilkinson功分器是由对称的上下两支路构成，是一个典型的3端口器件：

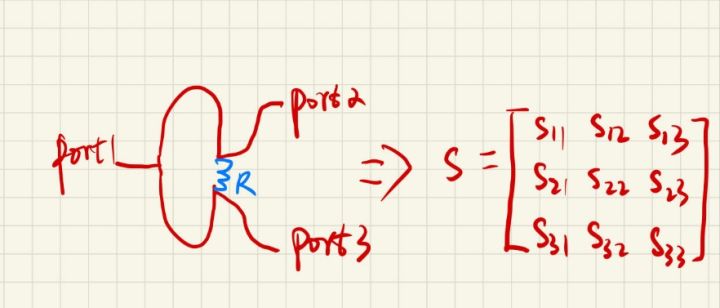
​如果纯粹地按照上面的S参数矩阵去硬分析，大兄弟，咱们怕是就go die了，不是说分析不了，确实是有点复杂了，因此我们在射频微波电路的设计中，为了简化分析模型，常常会采用基于对称轴，进行分析的奇偶模法来分析微波电路的传输特性。

本文中的功分器中我们就是为了减小分析的复杂度，分别采用奇与偶模去得到相关参数，最后推导出整体电路的S参数，这样分方法在有源电路里面同样适用，比如用差模共模法去分析差分电路，当然用理想的电壁和磁壁去分析对称的矩形波导结构也是不在话下的。

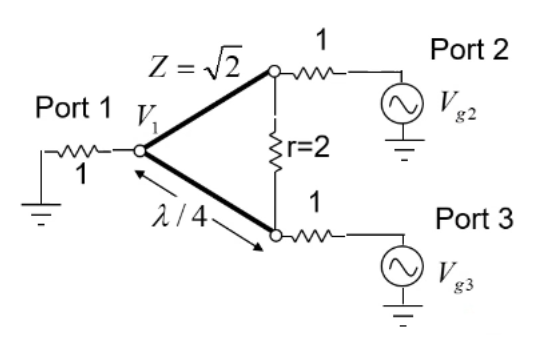
言归正传，我们怎么去分析如下图所示的Wilkinson功分器呢？（大家在看《微波工程》或者网上其他资料，如果还有点疑问的话，那么现在请跟上抛砖的节奏，咱们争取3分钟内解决战斗）

第一步：

先要明白，我们干这么一件事情的目的是什么：基本的需求就是求解在使得各个端口匹配的情况下，用精简的分析模型去分析其网络响应关系（可以换句话说，我们怎么求Wilkinson功分器的S参数矩阵）。

好了，有了上面的问题作为分析的大前提，我们现在又要搞清楚一个问题：如何去求解射频微波网络的S参数矩阵的？

这个就是基础性的东西，求解S参数，我们无外乎就是在一个端口加激励，然后去看想要观察的端口的响应。比如我们常常所说的S21，那就是在1端口加激励，2端口去看响应。

​那么我们令端口2和端口3的信号大小分为：

Vo2=1/2*（Ve+Vo）

Vo3=1/2*( Ve-Vo)

然后我们想办法，利用线性叠加原理，求解出在端口1的响应电压，然后我们就可以得到相应的S参数矩阵。好了，大概的思路有了之后，我们开始对Wilkinson功分网络进行分解。

第二步：

根据Wilkinson功分网络的对称性，首先我对传输线的特征阻抗，端口阻抗进行归一化处理（方便后面我们写算式），然后我们在中心对称轴对其进行剖分，得到如下所示电路：

​第三步：

我们分别来对奇模、偶模的情况，对电路进行拆分，方便后续进行相应的分析。

对于偶模而言，我们对端口2和3分别馈入2V0的电压（即令Vg2=Vg3=2V0），此时由于2,3端口电位一样，即可得到电路分析模型如下：

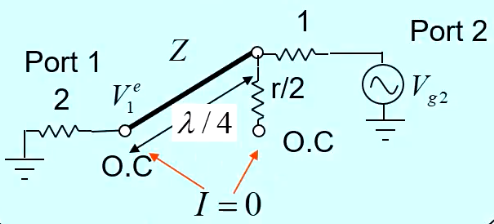
​对于奇模而言，我们对端口2和3分别馈如V0的电压（即令Vg2=-Vg3=2V0），此时得到如下的电路：

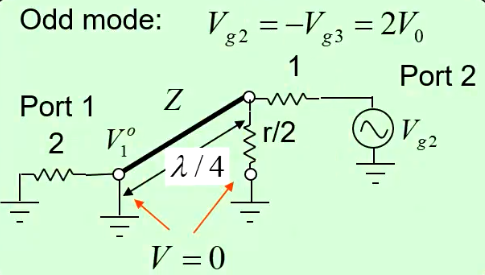
​第四步：

针对第三步中的电路模型，我们分别给出奇偶模模型对应电路端口相应的传函响应。

对于偶模，我们对其假设了端口2的电压为2V0（端口三与其相同，又是对称的，所以我们只要分析出2的激励情况，对于端口3的情况一目了然）

​此时端口2的归一化内阻为1，对于中间的隔离电阻，此时处于开路状态，因此可以对其忽略，为了让端口2处于匹配状态，在上图1点往左看的电阻应该为1，对于一个1/4波长阻抗变换器，端口1的电阻又为2，那么为了实现良好匹配，1/4波长的特征阻抗Z==，说完阻抗，那么对于端口2的激励到了端口1又是怎么样的呢？此时我们可以把1/4波长传输线的ABCD矩阵给求出来，然后，我们可以把端口2那个位置的电压通过ABCD矩阵转换到端口1处，对于一个传输线的ABCD矩阵实际上是十分简单的：

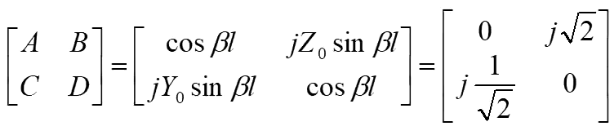
​所以，此时我们可以得传输线两端的转换关系：

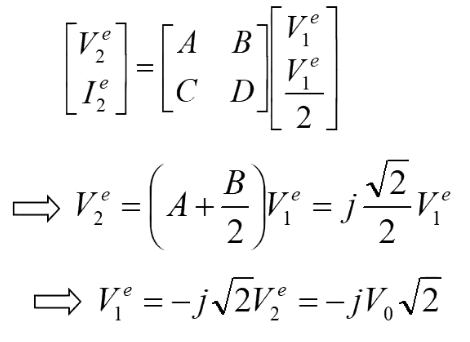
​由于端口2与端口3完全对对称的，所以此时：

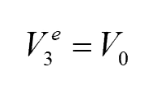
​（题外话：读到这里大家应该就可以明白为啥我们要假设Vg2和Vg3的电压为2V0了吧，主要还是考虑到分压情况，使得在传输线后的端点处的电压为V0，这样我们分析是的解析式更加简洁方便一点，当然这是上帝视角，是站在已知结果的基础上的假设，大家假设其他值也是完全没有问题的）

对于奇模，我们对其假设了端口2的电压为2V0，端口3的电压为-2V0：

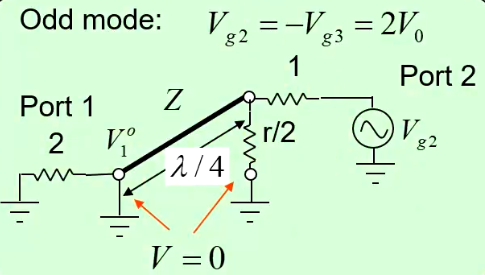
​由于在输入口的端点短路接地，即

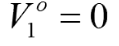
​经过1/4波长传输线变换，就成了开路，此时在传输线右端点的电阻无穷大，因此port2为了匹配，r/2的值就应该等于port2的阻抗值，即r/2=1，即此时r=100Ω（大家应该清楚为啥是100欧姆了吧），

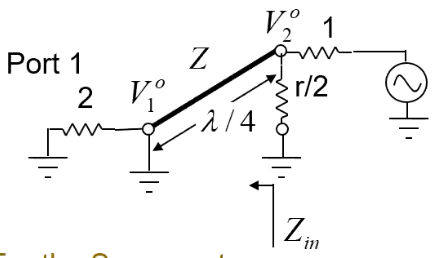
​然后我们继续把端口2（port2）的电压分压到传输线的右侧端点，即：

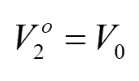
​所以此时端口3下方，在传输线右侧端点的电压：

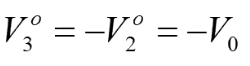
​第五步：

根据上面求得的端点电压，然后根据线性叠加原理，我们可以求得S参数的具体值，并最终得到S参数矩阵：

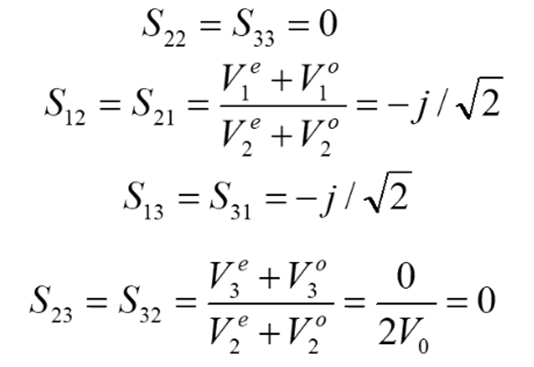
​即，此时

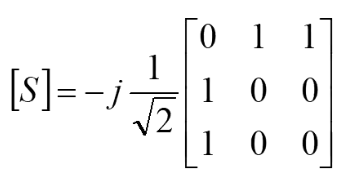
​好了，到目前为止我们就完成了对Wilkinson功分器的分析，相信大家对隔离电阻取值，传输线特征阻抗的认识稍微加深了一点，如果还有什么不明白的，欢迎加入微波射频网的交流沟通的群。

—— END ——