射频微波芯片设计6：射频电路中的噪声概论

《射频微波芯片设计》专栏适用于具备一定微波基础知识的高校学生、在职射频工程师、高校研究所研究人员，通过本系列文章掌握射频到毫米波的芯片设计流程，设计方法，设计要点以及最新的射频/毫米波前端芯片工程实现技术。

噪声的表达

说到噪声，大家应该还是比较熟悉的，这或许是我们射频模拟电路工程师又一个不可绕开的话题。当然谈到模拟电路，一般来说我们会说模拟电路有四大块组成：基带、射频、传感器、电源，其中除了电源外基本上都会重点去讨论信号与噪声的概念，因此对噪声的分析显得格外重要。而电路里面的噪声又极为复杂多样，就算到了后摩尔时代的今天，有些基本的噪声理论都还没有完全搞清楚，还是老规矩，本文旨在抛砖引玉，简单聊下射频电路中的噪声，欢迎大家讨论交流，共同进步。

噪声系数主要是衡量噪声大小的一个指标，当我们对电路里具体产生的噪声来源不清楚时，可以按照黑盒子定义法，把其直接定义为输入信噪比与输出信噪比的比值：

为了在实际工程中表示方便，我们通常采用dB值来表示噪声，即对上面的噪声F取一个对数

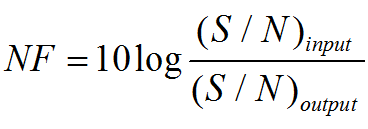
噪声的来源

可能看完上面的表述，较真的朋友们就会犯嘀咕了，既然模电里面除了电源外基本上都会重点去讨论噪声，那么我们可不可以，能不能够简单讨论下电路的具体噪声来源啊？？？

本文简单地归类下电路里面的主要的噪声来源，如下图所示：

 

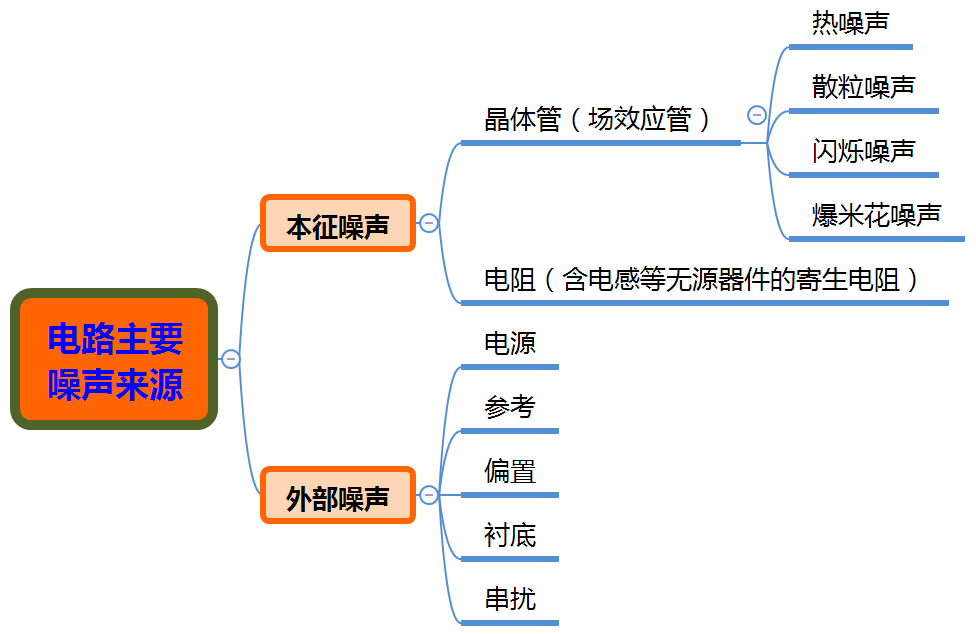
本征噪声是电路本身带来的噪声，主要由晶体管（场效应管）和电阻带来，而外部噪声主要是供电，参考，衬底干扰和串扰（模块间串扰，外部耦合等）。当我们在设计射频低噪声放大器时，主要考虑的是本征噪声带来的影响；而在设计低相位噪声放大器时，除了本征噪声，更为重要的是需要考虑外部噪声给放大器带来的相位噪声的恶化。

针对上述噪声来源，电阻主要是热噪声，我们简单讨论下其基本概念：

热噪声，这个概念大家应该比较好理解，毕竟咱们可以望文生义，一个“热”字就代表了其噪声的产生机理。那么到底是谁热？怎么热的？到底有多热？热和噪声到底有什么不可告人的秘密？

下面来简单探讨下下。首先来说说，到底是谁“热”的问题。简单地来说是电子比较“热”，我们知道在对放大器上电后，晶体管或者场效应管的偏压结内部的载流子会按照我们所加的电压，朝着指定的方向运动，然而现实是打脸的，因为我们的电子一生爱自由，虽然被外部邪恶的电压势力给指定了方向，但是一旦时机成熟，外部温度变化，我们的电子大兄弟就爱朝着非规定方向Run起来，因此，此时受温度影响朝着非规定方向Run起来的电子就是我们的热噪声的主角。下图简单示意了下电子是怎么“热”起来的：

 

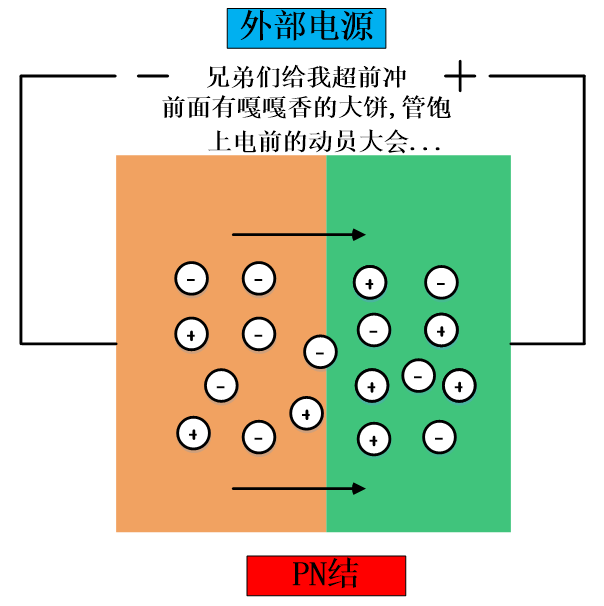
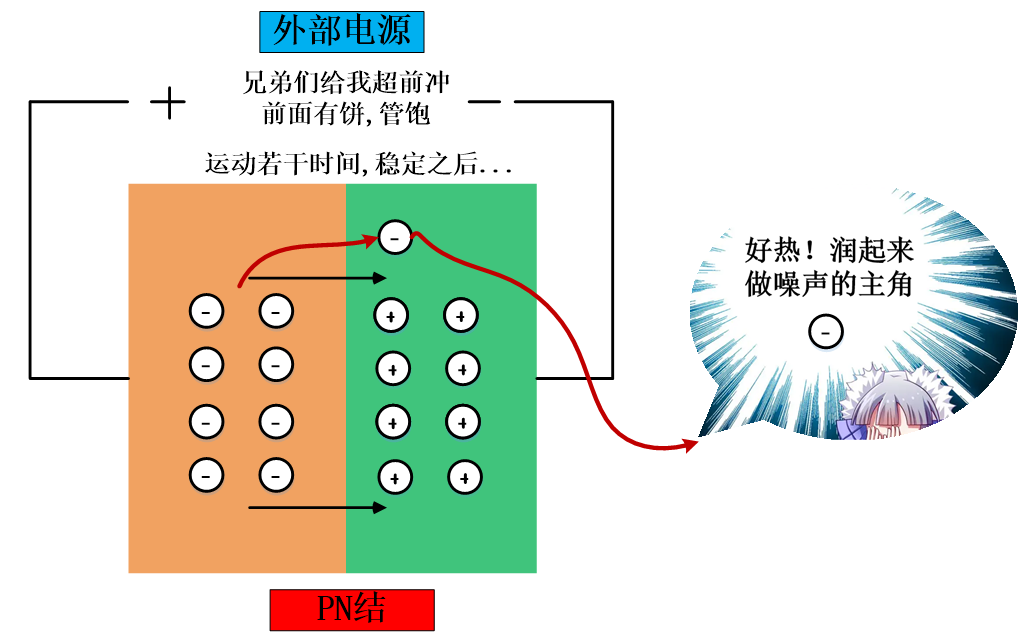
好了，回答完了在电路里面的热噪声，谁热，怎么热的问题，下面简单回答下有多热以及热和噪声的关系。

说到定量研究，我们一般比较科学的方法便是先去把热噪声给测试出来，然后根据相关值去具体表达热噪声，然后再去反复验证，最后得出结论。研究中，我们一般会采用等效法，根据下图所示的基本原理，我们首先把LNA（当然其他有源电路也是一样的）等效为一个热噪声源，那么表示热噪声便是测量其产生噪声的器件的平均噪声功率。我们可以采用下图中的电路结构去完成测试，通过改变负载电阻R的值，使得测到的噪声功率最大。根据最大功率传的原理，我们可以得到等效的热电阻。

 

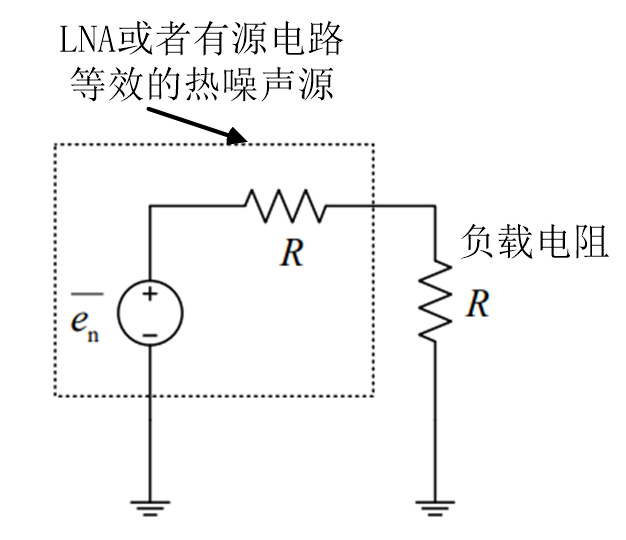
为了朋友们不打瞌睡，我们直接忽略中间的推导过程，这里给出结论，常见的电阻热噪声公式为：

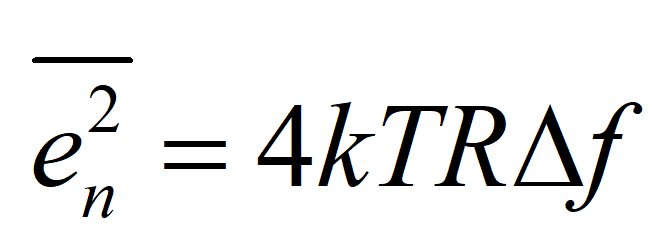
即热噪声的电压均方值与温度，电阻值，带宽成正比（需要注意的是，这里与带宽成正比并不是说热噪声的形成与频率有关，这里只是一个对频率积分求功率谱密度的过程，实际上的热噪声是电子杂乱运动导致的，和频率无关）。上述是在频域中测得的功率谱密度去定义热噪声，后续我们还会讨论在时域怎么去定义噪声。

散粒噪声（shot noise），也可以叫做散弹噪声，这个噪声怎么理解呢？追根溯源我们发现，其原因是在电子传播的时候具有离散性。这好比我们规定的传播方向上有用的电子按照既定路线行军，但有一小波电子由于离散性（符合泊松分布），虽然是按照外部电势朝向运动，但是还是开了一个小差，最终没有到达我们想要的位置上，是不是有点类似两个小年轻友达以上，恋人未满的感觉。为了尝试形象地解释下，我们看下图说话：

根据散粒噪声产生的两个必备条件，我们可以这样一个结论：单纯的电阻没有散粒噪声，或者，场效应管的栅极到沟道没有散粒噪声，大家应该没有什么意见吧。当然有意见的朋友们，也可以加小编好友他会拉你去群里去聊聊天，喝喝茶。同样的道理，我们又一次省去让人打瞌睡的推导过程，这里直接给出散粒噪声的数学表达式：

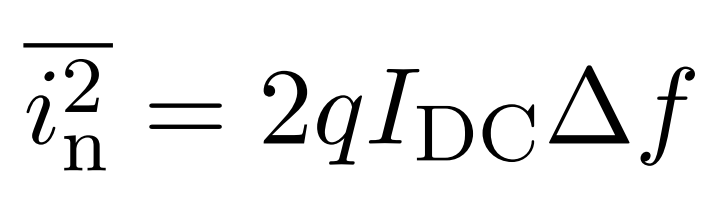
其中IDC就是我们刚刚提到的散粒噪声先决条件之一的直流电流，引入电荷q到表达式，主要也是因为电荷的颗粒性或者说离散性贡献了相应的噪声。

闪烁噪声，从数学层面上来说其是一种非平稳随机过程，其功率谱密度函数在频率低端（f接近于零频）发散，理论上在低频端的噪声谱密度可以到无穷大。从物理层面上来说，我们也把闪烁噪声叫做1/f噪声，没错，它就是大名鼎鼎的1/f噪声，那么它是怎么形成的呢？据笔者了解到的，目前还没有哪位大咖能给出一个标准的答案，大多都是模糊地说是由器件本身决定的，其特征在于噪声功率频谱密度与频率f成反比，当然在拉扎维大师的《RF Microelectronics》一书中给出了MOS管的1/f噪声经验公式：

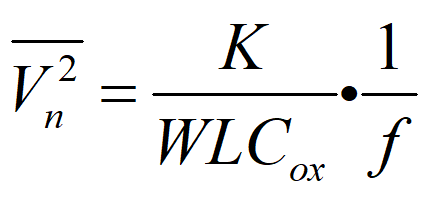
其中K是与制造工艺相关的参数，其大多为经验值，是根据每个工艺不同会有不同的取值，同时拉扎维老师还指出，同一个工艺条件下PMOS的K值一般是小于NMOS的，这也是之前我们博客中聊到的用PMOS做负载减小1/f噪声的原因。随着时代的进步，大家对1/f噪声的产生机理研究得越来越深入，以MOSFET管子为例，业界比较认可的1/f噪声主要是由栅极载波数波动（carrier number fluctuations ，CNFs)导致的。CNFs噪声是由于载波交换引起的近界面栅介质陷阱，栅极电介质中的电荷波动可能也会引起载流子迁移率的波动，上升到所谓的相关迁移率波动（CMF），进而引入了1/f噪声。当然，笔者目前还是没太整明白，也期待大家伙儿去研究研究，争取早日搞清楚这个底层机理，这样我们设计电路的时候也可以根据噪声产生的源头，由底层机理去减弱1/f噪声的影响，而不是根据经验和观察到的现象去减小1/f噪声。

不过可能有朋友又会问，这个1/f噪声不是在低频比较明显吗，那对我们做射频的，又何患之有？？？

其实这个我们在之前的博文中也聊到了零中频接收机中的1/f噪声对系统的影响，除此之外，在部分射频电路中也会有1/f噪声折叠到高频的隐患，因此大家伙还是要多多留意1/f噪声，尽可能地减小其对电路的影响。

爆米花噪声，我们也把此类噪声叫做爆发性噪声（burst noise）。该噪声在掺金的双极型晶体管中被发现有很高的强度，因而被认为与金属离子有关。不过与1/f噪声一样，我们对其产生的物理机理还并不是特别清楚，归纳下学者的研究，大家比较认可的一个原因是：由金属离子两个或两个以上（以两个为主）的离散态之间随机地切换导致的，当这类状态其切换时其频率在音频范围内，并会伴随boom，boom类似爆米花的声音，因此我们把这个噪声叫做了爆米花噪声。

上面的公式给出了，爆米花噪声的经验公式，其中K主要是由工艺和偏置决定的，而fc是拐角（corner）频率，当所在频率低于fc时，爆米花噪声功率谱密度变得平缓，也就是与频率相关性降低（甚至可以说是此时与频率无关）。

外部噪声，在上文我们也提到了，外部噪声主要有电源、偏置、参考信号、衬底耦合以及串扰信号等等，这类噪声通常也会被引入到电路之中，我们设计的时候需要相应地去考虑对策，比如偏置电路提高Q值，比如衬底加隔离墙等等。

噪声的大小求解

当我们整体衡量电路的噪声大小时，可以通过时域去分析也可以通过频域。从时域上来看，可以通过概率密度函数来表示噪声功率谱密度，一般而言，噪声符合正态分布，当然也有例外，比如上文说到散弹噪声（shot noise）符合泊松分布。

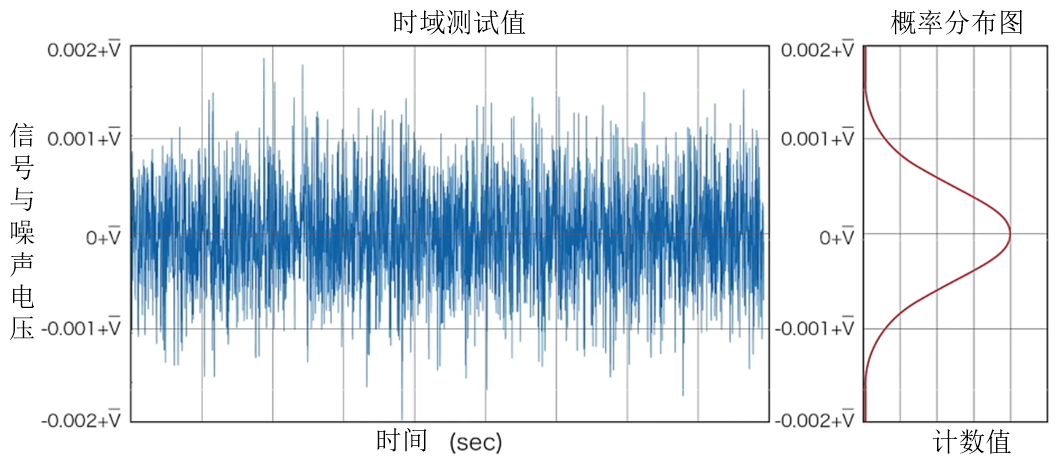
一般我们会对，信号V在时域上面采样分析，先把信号本身在采样点内的均值 求出来，然后再求其均方差，均方差δ基本上就可以反应我们的噪声啦（仅考虑噪声对信号的影响），求其信号均值的公式如下：

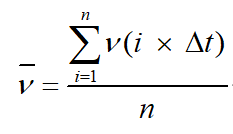
根据上面的n次采样后求得的信号均值，然后我们可以求得信号的均方根（Root mean square，RMS）误差，此时不考虑谐波分量对信号功率谱密度的影响时，通常均方根误差便可以表示我们的噪声。一般99%以上的信号与噪声都分布在信号均值±3δ以内：

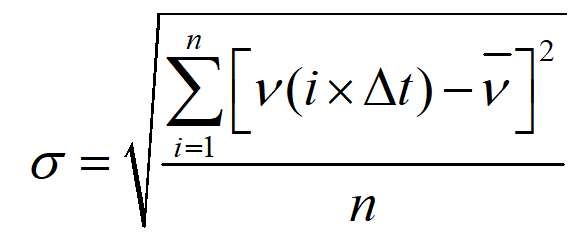
当然，除了通过时域求解电路里面的噪声，还可以通过频域噪声功率谱密度（这也是我们仿真工具，如ADS，AWR，Cadence中常用的仿真噪声-频率的求解方法）求解噪声。如下图（a）所示，我们对所求频率10KHz处1Hz带宽的信号进行采样（中心频率10KHz，带通滤波器带宽1Hz），通过功率计得到信号的功率，同理可以逐点推广到整个频段，如图（b）所示。

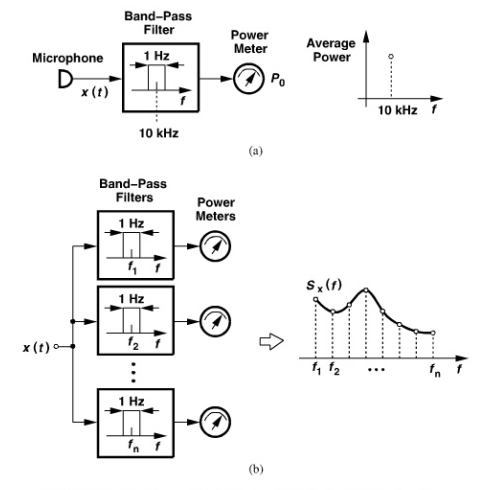
图片来源：拉扎维《RF Microelectronics》第二章

根据上图（b），Sx（f）函数便是功率谱密度，根据这个功率谱密度函数我们积分就可以得到功率的均方根误差，也就是我们的噪声。

好了，我们这里就讨论完了噪声大小的计算方法，接下来我们再来讨论一个有意思的话题——噪声叠加。恰好有机会看到RFASK上面有篇博文分享了《浅析多通道接收单元噪声系数的测试》，这是一个比较有讨论价值的话题，这里也要特别感谢RFASK提供了一个百家争鸣&分享交流的平台，本文就狗尾续貂，接着来简单谈论下噪声叠加的问题。

为了讨论简单化，本文就先假设有两个（两路）噪声叠加，令讨论的噪声电压分别为n1(t)与n2（t），针对单位电阻的平均噪声功率计算公式，我们可以求得两个噪声叠加后的平均噪声功率：

根据上面的公式，我们可以得到这样一个结论：当两个噪声系数不相关时，叠加的噪声总噪声功率可以直接把两个噪声功率直接相加，即上图绿色框框内的积分为0，即Pav=Pav1+pav2，也就是此时两路叠加的噪声比原来未叠加的单路噪声高了3dB；但是当两个噪声相关时，叠加的总噪声不再是两个噪声功率直接相加，还要考虑乘积项的积分项，我们假定两路噪声全相关，即令n1(t)=n2（t）,此时Pav=4*Pav1=4*Pav2，也就是此时两路叠加的噪声比原来未叠加的单路噪声高了6dB。那么四路或者多路噪声叠加的问题，大家可以自行下来推导。在实际电路中怎么去判断噪声是否相关，大家还得根据我们上文分析的噪声的来源去考虑。

本期关于噪声的讨论就到这里，感谢你耐心看到此处。

——END——

作者：RFIC_抛砖​