深入解析GNSS，打造更高精度、更高效的导航定位

作者：Andrew Brierley-Green, Maxim Integrated核心产品事业部资深工程师

现在，我们可以通过智能手机轻松确定位置和方向，如果回想古代探险家绕着圈子找路，尤其是在远离陆地的海上时，就会感到现在的导航技术更加神奇。早期导航依赖于星座，然后利用六分仪测量纬度。到19世纪末期，天文钟被广泛用于天文观测，以确定海上经度。卫星进入导航应用始于1964年，即Transit系统(称为NAVSAT或NNSS)。现在，在20,000km高空地球轨道上运行的31颗卫星组成了美国的全球定位系统(GPS)，为全球任何持有GPS接收机的人提供导航。

GPS系统的基本原理是卫星发射无线电信号，在地球或接近地球的位置接收。卫星在任何时刻的位置是已知的，根据卫星发射无线电信号的传输延迟，可计算出接收机距离每颗卫星的距离或“行程”。知道距离各个参考点(即卫星)的距离后，即可计算得到接收机的空间坐标。

图1. 类似19世纪末期的航海天文钟，当今的卫星导航系统帮助我们寻找道路

GPS系统包括三个部分：空间(卫星)、控制(地面站)和用户(接收机)。空间部分是卫星星座。GPS核心星座为24颗卫星组成的基线，每颗卫星大约12小时绕地球一周。该系统有6个轨道平面，每个平面4颗卫星，以及轨道上的备用卫星。在控制部分，地面站负责监测卫星，收集其在轨道上的位置、卫星时钟误差以及大气造成的信号延迟等信息。收集的信息被注入到卫星，然后再以导航消息的形式发送到地面接收机。

卫星为定位提供参考点，需要知道卫星在地球轨道上的准确位置。卫星绕地球运动的椭圆轨迹取决于地球引力。而由于月球和太阳的引力作用、太阳辐射压力以及地球的不均匀密度等因素，存在一定的影响。在估算卫星位置时，为了获得足够精度，需要准确测量轨道摄动。

GNSS接收机确定三个空间坐标和接收机时钟偏差。三边测量定位技术利用圆和球面的几何学，根据测得的与每颗可见(地平面以上)轨道卫星的距离，确定绝对和相对位置点。例如，如果计算得到与某颗卫星的距离为20,450Km，就知道接收机一定位于以该卫星为中心、半径为20,450Km的球面上的某个位置。如果计算得到与第二颗卫星的距离为19,760Km，就知道接收机也一定位于以第二颗卫星为中心、半径为19,760Km的球面上的某个位置。因此，由于两个条件同时成立，接收机一定位于两个球面的交汇处。根据几何学，两个球面的交点是一个圆，所以这就把接收机的位置限定在圆上的某个位置。将本例扩展到第三颗卫星，即可将位置限定在两个圆的交点，即两个点。如果其中一个点是无意义的，例如地球内部400Km，那么即可将其排除，接收机就必定位于另一个点。

卫星轨道可通过一组轨道参数表示。例如椭圆离心率就是其中一个参数。如果没有随机摄动，可根据轨道参数计算得到卫星任何时刻在轨道上的位置。表示轨道数据的通用术语是星历。NAV包含星历，以及获得星历数据时的时间(epoch)。地面监测站定期测量每个卫星的星历，并将该数据注入到每颗卫星。每颗卫星在NAV中广播其星历数据和epoch。由于摄动的原因，轨道参数存在一定的不准确性。所以NAV包括其轨道摄动的修正因子。

每个卫星发射一个唯一的伪随机噪声(PRN)码，随机码是一个重复的序列码，重复周期足够长，具有与真随机序列类似的统计特性。凭借PRN码，接收机就能够将信号与卫星关联起来。为简单起见，假设接收机知道接收的是哪颗卫星的PRN，接收机即计算本地产生的PRN副本与接受到的PRN的自相关函数。通过重复移位本地随机码副本并计算自相关，接收机最终将找到最大相关系数1.0。为了解析从卫星接收的数据，接收机必须将本地随机码副本与接收到的随机码同步。一旦接收机知道必须将本地测距码副本移多少位才能获得与接收代码的最大相关系数，也就知道了信号传输延迟(模1ms)。有一个“1%分辨率”经验法则，说明实测延时的分辨率可达到1%。GPS L1 C/A码是最常用的民用GPS信号，所有民用接收机都能解码，PRN码的码片率为1.023 Mcps。相关处理支持测量延迟精度为1%码片，对应于0.01/1.023x106 = 9.8 ns。在光速下，对应的距离精度为2.9m。

PRN码的另一作用是扩频调制。由于所有卫星都同时以相同的频率发射信号，必须有一种方法防止这些信号彼此干扰。所选的PRN码使任意两个码之间的互相关系数非常低。对于两个不同的PRN码，两者之间的滞后为任意值时，将这两个PRN码相乘，并对结果进行积分，将产生一个非常小的值。

误差源

计算与每颗卫星的距离时，只是将无线电波的传输延迟与自由空间传播光速简单相乘。然而，这并不能提供真正的距离，而只是给出一个的估算距离：“伪距”。例如，在信号从卫星到接收机的过程中，大部分时间通过的是自由空间，但也要通过地球的大气层。相对于信号在自由空间的速度，信号在大气层的速度将变慢，这就造成计算的距离存在误差。为了产生精度足够高的距离估算值，必须对这些误差因素进行补偿。

每颗GPS卫星都带有精度非常高的原子钟。所有卫星均同步到 “GPS时间”这一公共时基。然而，相对于GPS系统时间，原子钟存在一定的漂移和偏移。由于距离测量基于时间测量，时钟误差将引起距离测量误差。为了进行时间误差修正，地面站监测卫星时钟相对于GPS时间的误差，计算修正项，并将其注入到卫星。随后将在NAV广播。接收机利用从卫星接收到的修正项，有效补偿卫星时钟相对于GPS时间的偏差。

另一项较大的误差源是本地接收机时钟偏差。然而，由于这种偏差是所有从可见卫星上接收的信号所共有，可以计算得到并进行补偿。三个空间坐标和接收机时钟偏差是接收机需要求解的4个变量。所以，准确定位要求至少4颗卫星。

电离层误差来自自由电子的离子化等离子体和带电原子(离子)，范围为海拔50至1000Km，由于太阳紫外线的原因，从原子剥离出电子。电离层随每年季节、每天时辰以及在地球上位置的变化而变化。密度通常在中午前后较高，并且地球在其轨道中最接近太阳时也是如此。更复杂的是，电离层有多个层次，各层对信号的影响不同， 且各层在一天中也发生变化。如果某颗卫星靠近地平面，信号就必须通过更多的电离层，延迟进一步增大。充分利用载频对无线电波延迟的影响，可解决这种较大的随机变化延迟：频率越高，延迟越小。从同一卫星接收的两个载波信号将穿过相同的电离层，延迟不同。通过测量延迟差，即可计算得到绝对延迟。因此，多载波接收可以提供更高精度的电离层延迟测量，有效降低最大距离误差源。地面控制网络利用双载波技术定期测量地球上不同地点的电离层延迟，将修正因子注入到卫星，然后在NAV消息中广播到接收机。如果使用单载波接收机，则必须依赖于电离层模型，根据频率修正电离层延迟。然而，这种方法的精度不是特别高，因为模型往往只每天更新一次，且最近的地面站可能在数千公里之外。

多径干扰是另一需要解决的误差源。理想情况下，无线电信号直接沿着从卫星到接收机的视线通路传输。但是，尤其对于接近地平线的卫星，信号很有可能受到障碍物的反射，例如建筑物和树木。通过天线设计和使用遮蔽角等技术，可减轻多径误差。天线使用垂直接地天线防止接收到地面反射的信号。扼流圈天线可衰减地面反射的信号接触到垂直接地天线边缘时发生的表面波。遮蔽角忽略地平面上仰角小于某个角度(通常为15°)的卫星，因为此类卫星更容易受多径干扰。

GNSS卫星由于其较高速度和高度的原因，如果不进行修正，这些影响会导致系统无法使用。在GPS接收机和智能手机普及之前，相对论一般并不影响我们的日常生活。根据爱因斯坦的狭义相对论，当运动参考坐标系接近光速时，时间变得越来越慢。将该理论应用到卫星，当卫星以相对于地球的时钟高速运动时，卫星原子钟比地球表面的静止时钟“嘀嗒”的慢。可利用洛伦兹变换计算时间延展：

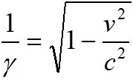
式中：

v = 卫星速度= 4Km/s
c = 光速= 2.998 x 10⁸m/s
1/y = 相对时间膨胀= 10^-10

所以，卫星时钟比地面时钟慢大约10¹⁰分之一。在一天中，这一差异累积达到7µs。现在，根据爱因斯坦的广义相对论，重力会使时间延展，时钟在较高重力变慢。将该理论应用到卫星，我们可以推测，由于卫星高度，其重力比地球表面时钟重力小，所以其时钟走的较快。计算这种影响的重力时间延展公式如下：

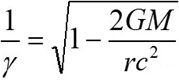
式中：

G = 万有引力常数= 6.674 x 10^-11 Nm²/Kg²
M = 地球质量= 5.974 x 10²⁴Kg
c = 光速= 2.998 x 10⁸m/s
r = 地球质心到卫星的距离
1/y = 相对时间延展

如果我们通过近似来简化方程并计算地球表面时钟与GPS轨道时钟的1/y之差，可得到下式：

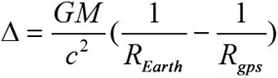
式中：

R_Earth = 地球半径= 6,357,000m
R_gps = GPS卫星轨道半径= 20,184 x 10³ + R_Earth = 26,541,000m
∆ = 卫星和地球上观测者之间的时间延展差= 5.3 x 10^-10

每天累积为45.85µs。卫星的速度致使卫星时钟每天慢7µs，但重力使该时钟每天快46µs，所以最终的结果是每天快38.6µs。

GPS卫星使用的基频全部是10.23MHz，其它时钟都据此获得。例如，GPS L1 C/A码率为该频率的十分之一，即1.023MHz。

为补偿时间延展，卫星上使用的基频被调谐为10.229999995453MHz，而非10.23MHz。所以，从地球上观测者的角度看，卫星时钟的频率恰好是10.23MHz。

伪距中存在一个有意为之的误差源。最初，GPS卫星特意在发射粗码(C/A)信号中增加时变误差，以防敌人利用民用GPS接收机实现精确武器制导。这种特意降低性能的方法被称为选择可用性(SA)。SA误差通常在水平方向为50m，垂直方向为100m。然而，由于SA误差对某个地区的所有接收机具有相同的影响，如果我们利用GPS接收机和某个已知位置，就能够估算出SA误差，并将其发送给其它接收机。该技术称为差分GPS，该技术的应用造成SA失效，所以SA政策于2000年取消。

高精度定位技术

差分GPS (DGPS)提供了一种实现更高定位精度的方法，这对于测绘、农业和无人驾驶汽车等需要精准定位的应用至关重要。典型民用GPS接收机在水平方向可达到2-5m定位精度，但以上所述应用要求亚米级精度。利用DGPS技术，位于已知固定位置的静态参考点接收机计算每颗可见卫星的伪距，也计算定时误差。通过某种渠道将定时误差修正信息发送给附近的“漫游”接收机，后者可将修正信息作用到伪距计算。如果接收机位于参考点接收机的几百公里范围之内，参考接收机和漫游接收机接收的信号通过的大气层相同，所以具有相同的延迟。所有公共误差源都将被修正(多径误差除外，因为这些在接收机本地)。

基于载波的GPS是实现更高精度的另一途径。该方法使用无线电载波的相位而非PRN码来估算距离。利用1%精度经验法则，实测载波相位的分辨率可达到1%。对于GPS L1 C/A码，载频为1575.42MHz，波长为19cm，测量分辨率为1.9mm。这种方法的精度如此之高，致使参考接收机的位置必须考虑地壳构造板块的大陆漂移，为每年几英寸。

为您的设计选择最优的GNSS接收机

GNSS接收机通过处理卫星广播信号，确定用户位置、速度和准确时间(PVT)。如图2所示，典型GNSS接收机由以下部分组成：

· 天线
· 外部低噪声放大器(LNA，可选)，靠近天线位置的低噪声放大
· SAW滤波器(可选)，用于抑制干扰
· 温补晶振(TCXO)
· RF前端IC，对GNSS信号进行放大、下变频、滤波和采样
· 基带数字信号处理器(DSP)，实时接收计算通常在FPGA实现。DSP输出NAV位和信息，例如载波相位和码相位。
· 基带处理器子系统，负责执行所有的数学运算，计算导航参数、解析NAV消息以及应用修正

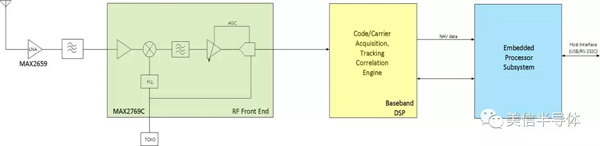
图2. 典型GNSS接收机结构

截至目前，我们在本文中讨论的是美国的GNSS。其它国家和地区开发的星群包括俄罗斯的GLONASS、欧盟的伽利略、中国北斗和印度IRNSS。每个星群都拥有自身的信号结构，使用不同的频带，当然有些是重叠的。表1所示为各种不同的卫星导航系统。

表1：全球卫星导航系统

在评估GNSS接收机时，确保首先考虑目标应用，这将影响您需要的功能以及性能、精度和功耗。例如，如果要求高精度定位，就需要支持多个频率和多个星群的接收机。Maxim拥有经过长期验证的GNSS技术，被多家世界顶级GNSS公司所采用。Maxim产品既包括GNSS RF前端IC，又包括GNSS LNA。例如，Maxim提供MAX2769——业界第一款可完全编程的通用GNSS接收器，单芯片即可支持GPS、GLONASS和伽利略系统。作为一次变频、低中频(IF) GNSS接收器，MAX2769集成单芯片滤波器，无需外部中频滤波器，并提供低至1.4dB的总噪声系数。也提供汽车级产品MAX2769B。MAX2769C单芯片通用GNSS接收器支持L1/E1、B1和G1波段，支持GPS、伽利略、北斗和GLONASS卫星系统。与MAX2769一样，MAX2769C (图3所示)也提供低至1.4dB的总噪声系数，不需要外部IF滤波器。

为实施完整方案，MAX2769C可连接到MAX32631等运行GNSS基带软件的微控制器，实现软件接收机。或者，将ADC采样信号输入到FPGA，在FPGA完成底层基带处理，以实现高性能、基于硬件的方案。

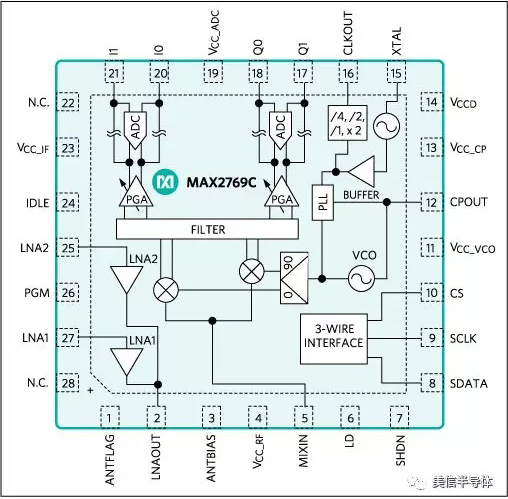
图3. MAX2769C框图

总结

目前，越来越多的电子设备提供位置服务，帮助我们实现全球导航，也根据我们所在位置提供更有用的资源检索。这些设备内部是复杂的GNSS技术，例如为我们提供需精确定位的接收IC。本文介绍了GNSS技术的历史背景，并讨论了需要修正的误差、实现更高精度定位的技术，以及支持多频段和多卫星系统的接收器IC。