专用短波接收机射频前端预选滤波器的设计与实现

1）将实际频率Ω归一化

得归一化幅平方特性

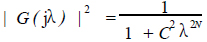（8）

由此可以看出|G（jλ）|²（或|G（jΩ |²）中只有2个参数C和N，N 是滤波器的阶次。

2）求C和N

由（5）式得

α（λ）= 101g（1 + C²λ^2N），（9）

则公式，

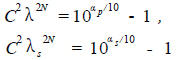（10）

因为λ_p = 1，所以

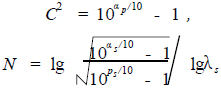（11）

这样C和N 可求。

若令α_p = 3 dB，则C = 1，这样巴特沃兹低通模拟滤波器的设计就只剩下一个参数N。

3）确定G（s）

因为p = jλ，有

（12）

由1 +（-1）^Np^2N = 0

解得

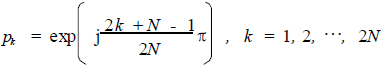（13）
 
这样，G（p）G（- p）的2N 个极点等分在s平面半径为一的圆上，相距为（π/N）rad。
 
为了保证所设计的滤波器是稳定的，应把左平面的极点赋予G（p），即
 
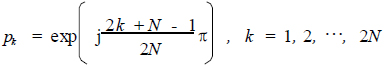（14）

这样

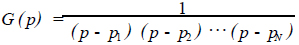（15）

若N 为偶数，G（p）的极点皆是共轭出现，即

p_k，p_{N +1 - k}，1 ≤ k ≤N /2 （16）

这一对共轭极点构成一个二阶系统，即

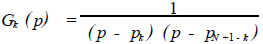（17）

总的转移函数应是N /2类型的二阶系统的级联，即

，N 为偶数。（18）

若N 为奇数，它将由一个系统和（N - 1）/2个二阶系统相级联，即

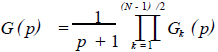，N 为奇数。（19）

这样，就得到了归一化的转移函数G（p）。利用式（7）关系，即得实际需要的G（s）。

为实现二端口梯形的转移函数G（s），重点在于利用G（s）求出z₁₁和z₂₂，然后实现z₁₁和z₂₂。转移函数的零点与z₂₁的零点相一致，所以不必求z₂₁。