现代无线电接收机的系统噪声系数分析一：级联接收机的计算

双边带噪声系数

有些情况下，两路响应同样有用，不适合使用术语“系统的主频率变换”。例子有辐射计和直接转换接收机。直接转换接收机中，LO频率位于有用信号的RF通带的中心，混频器的两路响应形成全部有用信号频谱的连续两半。这种情况如图5所示。

图5. DSB噪声系数。

所以，这种情况下就需要考虑双边带噪声因子：

如果我们假设G_s=G_i，那么：

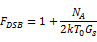
在相同约束条件下：

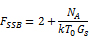
由此可得出结论：当转换增益相等时，混频器的SSB噪声系数比对应的DSB噪声系数高3dB。此外，如果混频器不增加任何附加噪声(N_A=0)，那么F_DSB=1或NF_DSB=0dB .

噪声系数在级联系统噪声系数计算中的应用

基线案例：线性电路模块的级联

考虑以下三个放大器模块简单级联的情况(图6)。

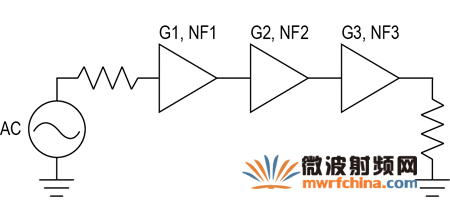
图6. 三个增益模块级联。

输出的总噪声可计算如下：

N_OUT=kT₀G₁G₂G₃+N_A1G₂G₃+N_A2G₃+N_A3

由于级联输入处的热噪声引起的输出噪声为：

N_OT=kT₀G₁G₂G₃

这意味着总噪声因子为：

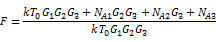
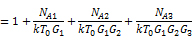
设：

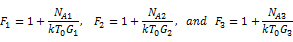
得到：

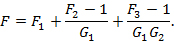
这可作为三个模块的标准弗林斯级联噪声公式。从该式很容易外推至任意数量模块的情况。

外差式转换级

考虑接收机信号通路中的以下频率转换级(图7)。混频器的双边带噪声系数为3dB，其转换增益为10dB。预期载频为2000MHz，选择LO为1998MHz，所以预期和镜像频率均在滤波器的通带范围之内。

图7. 无镜像抑制的外差级。

这种配置的级联性能汇总于表1，其中CF为通道频率；CNP为通道噪声功率；GAIN为级增益；CGAIN为至本级的级联增益，包括当前级；CNF为级联噪声系数。

表1.仿真的级联性能*

器件	CF (MHz)	CNP (dBm)	GAIN (dB)	CGAIN (dB)	CNF (dB)
CWSource_1	2000	-113.975	0	0	0
BPF_Butter_1	2000	-113.975	-7.12E-04	-7.12E-04	6.95E-04
BasicMixer_1	2	-97.965	10	9.999	6.011

* 滤波器无镜像抑制。

这两个模块的总级联增益为9.999dB，SSB噪声系数为6.011dB。这一噪声系数是可通过之前的分析正确预测到的，因为我们预期混频器的SSB噪声系数比DSB噪声系数高3.01dB。由于滤波器存在有限的插入损耗，所以噪声系数稍微变差。总体而言，这一结果满足我们的预期。

现在考虑相同的情景，但LO频率为1750MHz(图8)。LO频率为该值时，镜像处于1500MHz，正好处于混频器之前的滤波器带通范围之外。

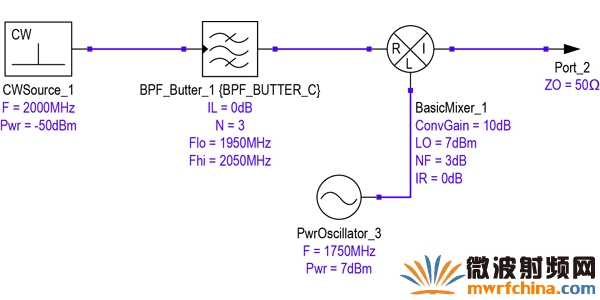
图8. 带镜像抑制的外差级。

这种配置的级联性能汇总于表2。预期信号的增益与之前相同，但是级联噪声系数(CNF)已经变为4.758dB。

表2. 仿真的级联性能*  

器件	CF (MHz)	CNP (dBm)	GAIN (dB)	CGAIN (dB)	CNF (dB)
CWSource_1	2000	-113.975	0	0	0
BPF_Butter_1	2000	-113.975	-7.12E-04	-7.12E-04	6.95E-04
BasicMixer_1	250	-99.218	10	9.999	4.758

* 滤波器具有显著的镜像抑制。

为解释这一结果，我们需要考虑本例中的噪声情景与图4中所述的情况类似，尤其是源阻抗镜像噪声得到了抑制。可利用之前推导的DSB噪声因子公式计算出混频器级增加的噪声：

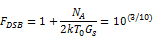
所以：

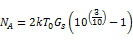
现在，混频器输出的总噪声可由式N_OUT=N_A+kT₀G_s+αkT₀G_i,计算得到，本应用中α=0。因此：

N_OUT=2kT₀G_s(10(^3/10)-1)+kT₀G_s

得到的噪声系数可记为：

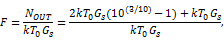
以dB表示，即得到：

NF=10log₁₀ (2(10(^3/10)-1)+1)=4.757dB

结果应该与仿真值4.758dB相当，其中包括滤波器插入损耗引起的微小附加噪声。

一般情况下，混频器级的有效单边带噪声系数可由下式给出：

F_SSBe=2(F_DSB-1)+1+α,

式中，当镜像频率下的端点噪声得到较好抑制时，α=0；当根本未抑制噪声时，α=1。注意，如果α=1，有效SSB噪声系数降低至F_SSBe=2F_DSB,，即本部分开始时所述的情况。在有些情况下，α的值会是小数，例如镜像抑制滤波器未直接耦合到混频器输入端，或者镜像和预期响应之间的频率间隔不太大。