有限带宽信号采样和混叠的数学分析

图1. 信号g(f)的频谱

接下来对g(f)进行采样。我们可以利用数学形式表示该操作，即g(f)乘以一个时间间隔为T的冲激函数序列。通过将g(f)与冲激函数相乘，我们得到对应于冲激函数发生时刻的g(f)值，其它任何时间的乘积都为零。这类似于以fSAMPLING = 1/T的频率对g(f)采样。该操作可用公式1表示，采样后的新信号称为s(t)：

下一步是找出已采样信号s(t)的频谱。通过对公式1进行傅立叶变换可得到：

计算上面的积分比较复杂。为了简化计算，注意到s(t)是g(f)与冲激脉冲序列的乘积。同时我们还知道时域的乘法对应频域的卷积。(关于这一结论的证明可参考任何有关傅立叶变换的资料。) 因此，S(f)可以表示为：

注意公式3中的星号表示卷积，而不是相乘。我们已经知道原始信号的频谱g(f)，因此只需要算出冲激函数序列的傅立叶变换。我们知道冲激函数序列是一个周期函数，因而可以用傅立叶级数表示。如下式：

其中傅立叶系数为：

公式5中积分的上下限只指定为一个周期。当处理冲激函数时，这没有问题。然而，为了使上面的表达式具有更好的通用性，可以进行如下代换处理：用一个从负无穷到正无穷的傅立叶积分代替该积分，并用单个冲激函数―t周期信号的基本信号替代周期性的冲激函数序列。因而，公式5可以改写为：

这样一来冲激函数序列可采用以下易于进行傅立叶变换的简化表达式：

考虑到一个信号可以从其傅立叶变换积分得到，如下式：

并且：

最终表达式如下：

根据以上结果，再重新考虑已采样的基带信号。其傅立叶变换表达式如下：

两个信号A(f)和B(f)的卷积定义为：

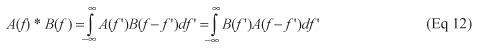
则S(f)可表示为：

计算的结果为公式13，通常称为采样定理。它表明在时域里按周期T (秒)采样得到的信号会以1/T的频率重复原始信号的频谱，如图2所示。这一结果反过来可以清楚且直观地回答先前的问题：如何采样模拟信号才能够保持原始信号的全部信息？

图2. 采样信号s(t)的频谱 

混叠效应

为保留原始基带信号的所有信息，必须确保每一个重复频谱“轮廓”之间不发生交叠。如果相互交叠(这种现象称为混叠)，就不可能再从采样信号中恢复出原始信号。这会使高频成分混叠到低频频段，如图3所示。

图3. 混叠对信号的影响

为了避免混叠，必须满足以下条件：1/T > 2，或1/T > 2BW。该结论也可用采样频率表示为：

因此，不会产生混叠的最小采样频率为2BW。这就是众所周知的奈奎斯特定律。

图3给出了产生混叠的采样信号。注意高频信号分量fH呈现为低频分量。您可以用一个低通滤波器来恢复原始频谱，并将其它频谱分量滤掉(衰减)。当使用截止频率为的低通滤波器恢复信号时，它无法将混叠的高频信号滤掉，从而造成有用信号的劣化。

考虑到混叠会恶化有用信号，再来考虑带通信号这类特定的有限带宽信号。带通信号的低频边界不是零。如图4所示，带通信号的信号能量分布在L与>U之间，其带宽定义为U - L。因此，带通信号和基带信号的主要区别在于它们的带宽定义：基带信号的带宽等于它的最高频率，而带通信号的带宽为最高频率和最低频率之差。

图4. 带通信号


从前面的讨论可知，采样信号以1/T的周期重复原始信号的频谱。因为这个频谱实际上包括从0Hz到原始带通信号低频截止频率之间的零幅值频带，所以实际的信号带宽要比U低。因此可以在频域内做一定的频率偏移，从而允许采样频率低于当信号频谱占据整个零至U范围时要求的采样频率。例如，假定信号带宽为U/2，采样频率取为U即可满足奈奎斯特定律，采样信号的频谱如图5所示。

图5. 带通采样信号的频谱

该采样过程没有产生混叠，因此如果有理想的带通滤波器，可完全从采样信号中恢复出原始信号。在本例中，注意到基带和带通信号的差别是非常重要的。对于基带信号，带宽和相应的采样频率只由最高频率决定。而带通信号的带宽通常都要比最高频率小。

以上特性决定了从采样信号中恢复原始信号的方法。对于最高频率相同的基带信号和带通信号，只要采用合适的带通滤波器来隔离原始信号频谱 (图5中的白色矩形部分)，带通信号就可以采用较低的采样频率。由于信号频谱中包括阴影部分，用于基带信号恢复的低通滤波器在这种情况下无法恢复出原始带通信号，如图5所示。所以如果要用低通滤波器恢复图5中的带通信号，采样频率必须在2U以上以避免混叠。

有限带宽信号必须在满足奈奎斯特定律的情况下才能被完全恢复。对于带通信号，只有用带通滤波器时奈奎斯特采样频率才可以避免混叠。否则就必须使用更高的采样频率。在实际应用中选择转换器采样频率时，这一点很重要。

还要注意的是对有限带宽信号的假设。从数学上分析，一个信号不可能是真正有限带宽的。傅立叶变换定律告诉我们，如果一个信号的持续时间是有限的，则它的频谱就会延展到无限频率范围，如果它的带宽是有限的，则它的持续时间是无限的。很显然，我们找不到一个持续无限时间的时域信号，所以也不可能有真正的有限带宽信号。不过绝大部分实际信号的频谱能量都集中在有限带宽内，因此前面的分析对这些信号仍然有效。 

采样正弦信号

采样正弦信号可以非常简单和方便地展示发生混叠时高频成分呈现为低频成分这一固有现象。纯粹正弦信号的频谱仅包括相应频点上的尖峰信号 (冲激函数)，出现混叠时，尖峰会从一个频点移到另一个频点。

以下结果是用125Msps、12位ADC MAX19541测试得出的。图6所示为输入信号频率fIN = 11.5284MHz时变换器输出信号的频谱。数据显示主尖峰正好出现在该频点上。频谱中还有一些其它的尖峰，它们是由转换器的非线性引起的谐波，和本文的讨论主题无关。由于采样频率fSAMPLING = 125MHz，远大于奈奎斯特定律要求的两倍输入频率，所以不会出现混叠。

图6. MAX19541 ADC采样后的信号频谱。fSAMPLING = 125MHz, fIN = 11.5284MHz.

接下来考虑如果把输入频率提高到fIN = 183.4856MHz，主尖峰的位置会发生什么变化。该输入频率大于fSAMPLING/2，可以想象会有混叠出现。图7给出了得到的频谱，主尖峰落在58.48MHz频点，这就是混叠信号。换言之，在58.48MHz频点出现了一个原始信号中不包含的频率信号。注意图6和图7中都只给出了奈奎斯特频率以下的频谱，因为频谱是周期性的，图中的显示部分已经包含了所有必要信息。

图7. MAX19541 ADC采样后的信号频谱。fSAMPLING = 125MHz, fIN = 183.4856MHz.