高速高频电路电磁场仿真：FDTD和FEM算法各有什么优缺点

以下是两位网友的回答，稍微有所调整：

RanHe的回答：

在讨论电磁仿真前，先要敬仰前辈。

计算电磁学从大的方向可以分为两大类：全波仿真算法，高频算法。

全波仿真是一种精确算法，但是非常消耗计算资源。一种简单的估算方法是：通常我们对物体要进行剖分，剖分至少要达到0.1个波长。那么也就是说，如果这个物体的电尺寸为10个波长，则有100*100*100=一百万个网格。每一个网格你还要存储大量的电磁参数，一般都是单精度浮点型。所以很容易就需要上百兆的内存。如果电尺寸有20个波长，那就需要上G的内存。如果物体的几何特征比较不正常，有很多的细微结构，则需要更密集的剖分，这样很容易就超过了普通计算机的计算能力。例如，1GHZ的波长是0.3米，GSM的频率大概位置，这样也就能对一两米的物体进行仿真。如果是3G通信，频率大概是2GHz,我们也就只能计算不超过一米的物体，而且不能有奇形怪状的结构。

高频算法就是为了解决这一问题而生的。对于军用系统，我们需要对飞机，舰船的电磁性能进行分析，按照前面的讨论，全波仿真显然不行。这样高频算法采用了很多近似，例如物理光学，几何射线法等等，进行近似计算。

FDTD（时域有限差分）、FEM（有限元）、MOM（矩量法）、FIT（有限体积分）都是属于全波仿真算法。其中，FDTD，FIT属于时域算法，代表软件EMPro和CST；FEM，MOM属于频域算法，代表软件ADS、EMPro和HFSS。 时域算法适合宽带信号分析，以为只要仿真一个脉冲输入，就可以得到很宽的带宽信息。而频域算法一次只能计算一个频点，适合窄带信号。

FEM与FDTD相比，主要是剖分精确。因为FEM是三角网格，而FDTD是四边形 。

以上两图很明显的说明了不同网格对物体的近似程度。第一个是FDTD，第二个是FEM。哪个计算结果准确，不用我讲了吧。

现在说说FDTD和FIT有啥区别。FDT2000D直接对微分方程离散，大家都知道，对于每一个网格，我们认为是均匀的。

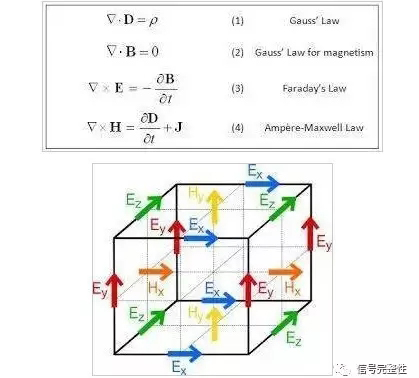
FIT是对积分方程离散，他是沿着积分曲线，取了好多电磁参数，适合处理分非均匀的介质，和交界面，相比FDTD更加精确。

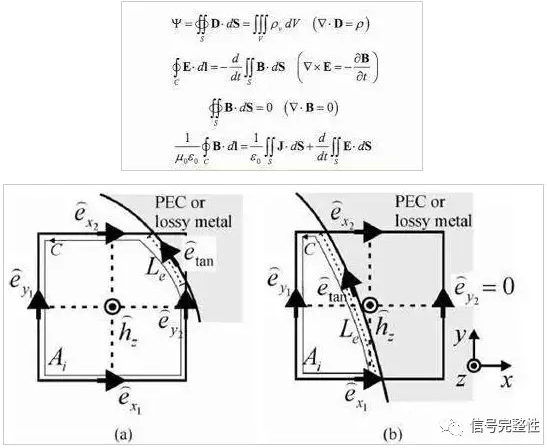
一身孜然的回答:

FDTD作为一种有限差分时间域数值计算方法，有一次性脉冲分析（宽频），自然结合非线性谐波分析、自然结合Lorentz , 导体等电介质的优势。缺点是处理高Q震荡时候需要花费相当长的时间（高Q震荡需要很久才会消失），此外它的空间差分方式单一，只能分割成长方体。对于非常规边界和材料形状的仿真有些力不从心。

FEM则基本克服了高Q仿真，长方体差分的缺陷，可以对空间进行任意分割（不均匀的四面体，例如）。但问题是，他一般是对单一频率频域进行仿真，因此对于脉冲源的仿真比较复杂，并且难以分析系统响应的波形，也难以分析非线性系统出现的谐频。对于宽频源的仿真需要更长时间。但对于高Q震荡的计算不在话下，频谱分辨率也可以达到任意高。