ADS信号完整性专题之串扰

鉴于国内外的很多ADS的资料都是微波射频领域的，接下来，我们会慢慢的分享一些ADS在信号完整性领域经常使用的小功能和技巧。今天给大家介绍使用ADS进行串扰的仿真。

关于串扰的理论，大家可以参照《信号完整性分析》《信号完整性揭秘》等书籍。

大家都知道，串扰与很多因素有关系，如传输线耦合长度、信号的上升时间、传输线的间距等等。这里就以这三个因素举例子对串扰做一些定性的分析：

在ADS中搭建仿真的拓扑结构，这一点非常的重要，因为要是拓扑结构搭建都有问题，那么就使得仿真结果变得不可分析，所以，在如下的仿真中，都尽量以单一变量做仿真实验。

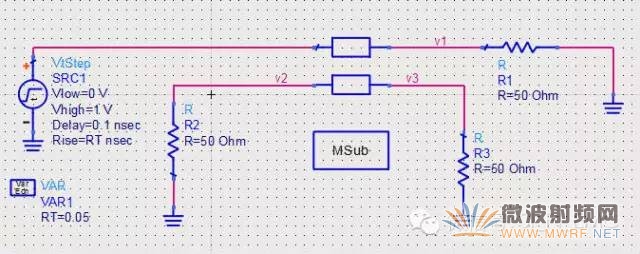
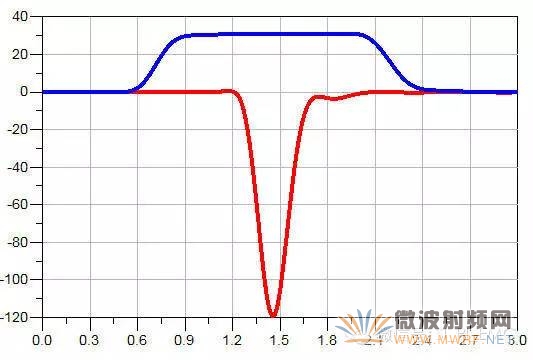
得到的串扰结果如下（蓝色为近端串扰NEXT，粉色为远端串扰FEXT）：

1、上升时间：考察上升时间时，其他的参数都不变，只改变上升时间的变量，所以需要加入变化参量和扫描参数，如下所示：

上升时间从50ps开始，300ns截止，每隔50ps仿真一次，得到的仿真结果如下：

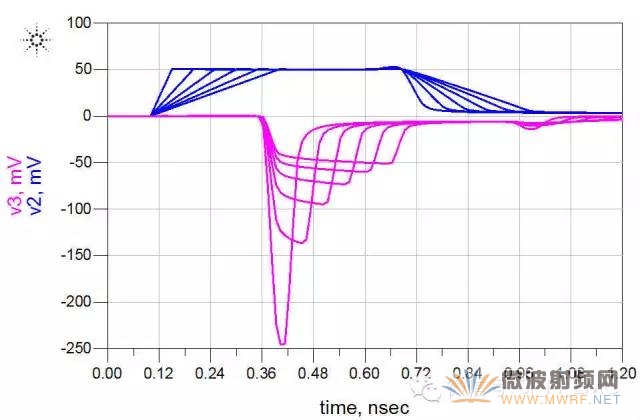
显然，随着上升时间边长，其远端串扰变小，饱和长度变大。

2、耦合长度：改变耦合长度，其他参数保持不变。长度由1inch开始，截止到6inch，每隔1inch仿真一次，变化参量和扫描参数如下：

得到的仿真结果如下：

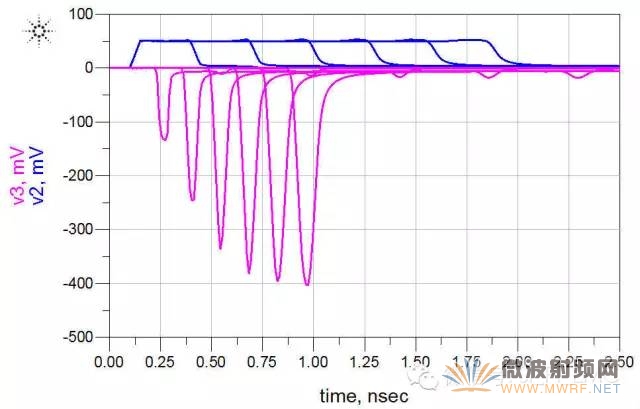
随着耦合长度的增加，其远端串扰一直在增加，在1inch之前就已经达到饱和长度，所以在此实验中，1inch之后增加耦合长度对近端没有影响

3、传输线间距：改变传输线间距，其他参数保持不变。间距由4mil开始，截止到10mil，每隔1mil仿真一次，变化参量和扫描参数如下：

得到的仿真结果如下：

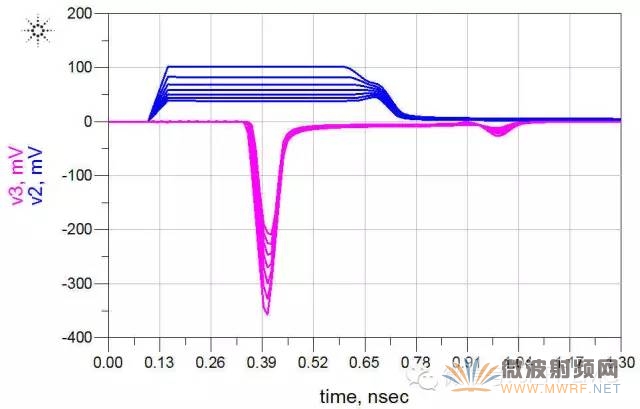
由仿真结果可知，其间距越大，其近端串扰和远端串扰都会变小。

由于ADS对数据的处理比较好，所以在以上实验中，还可以进行很多数据的测量，这里只是讲解串扰的参数sweep的仿真，所以没有对数据处理做进一步的阐述，后面会专门做一篇数据处理的文章。

很多时候我们都在死记硬背很多公式和结论，记得住也记得对当然很好，但是如果记不住也不知道对不对，还不如使用一些仿真软件对相关的问题进行仿真，这样我们可以自己得到很多实用的经验和结论。

欢迎关注：信号完整性（SI_PI_EMC）