一种结构新颖的双通带超导滤波器设计

闫鑫^1,2，季来运¹，张浩^1,2，李颢毅^1,2，王昭月^1,2，曹凤莹^1,2

（1.天津海芯电子有限公司，天津300380；2.天津师范大学物理与材料科学学院，天津 300387.）

摘要：本文基于双模谐振器设计了一款新型双通带高温超导(HTS)滤波器。双模谐振器由一个短路枝节和两个开路枝节构成，可以激发两个谐振频率。探究了谐振器枝节的物理尺寸对两个谐振频率的影响，通过合理设计双模谐振器各枝节的长度、谐振器间耦合间距、以及输入输出馈线的激励型式，完成了双通带超导滤波器的设计，滤波器电路在厚度为0.5mm的MgO基片上的DyBa₂Cu₃O₇高温超导薄膜上设计。该双通带滤波器的两个中心频率为350MHz和817MHz，其相对带宽分别为0.71％和1.93％。

关键词：双通带滤波器；短路枝节；开路枝节；高温超导薄膜

1  引言

随着通信行业的快速发展，能够满足不同通信频段要求的双频段通信系统受到越来越多的关注。双通带滤波器作为射频前端的关键部件，直接影响到系统的性能。随着高温超导材料和制造技术的快速发展，高温超导双通带滤波器以其插入损耗低、衰减陡峭、选择性好等优点成为近年来的研究热点之一^{[1, 2]}。

双通带滤波器的基本设计方法有三种。第一种就是将多个滤波器组合形成双通带。例如在[3]中，通过将两个带通滤波器并联形成双通带。在[4]中，通过将带通滤波器和带阻滤波器级联形成双通带。这种方法虽然在设计理论上相对简单，但是会使滤波器的尺寸增大，不利于小型化，而且还要考虑两个滤波器匹配所引入的额外损耗。第二种方法是耦合矩阵综合法。在[5-8]中，通过采用交叉耦合产生的传输零点，将单个通带分为两个通带。这种方法的优点是逻辑清晰，但耦合矩阵往往比较复杂。第三种方法基于多模谐振器^[9-11]，如阶跃阻抗谐振器、短截线负载谐振器等。这种方法虽然会使滤波器的尺寸变小，但是难以独立设计带宽。针对以上问题，本文提出了一款新型的双模谐振器。该双模谐振器由一个短路枝节和两个开路枝节构成，基于该谐振器结构完成了双通带超导滤波器设计。

2  双模谐振器的分析

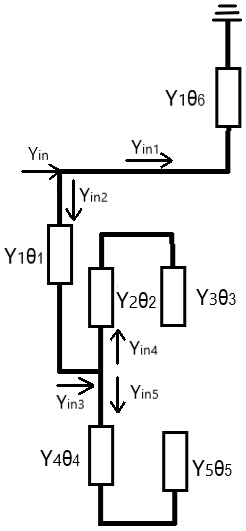
本工作要求滤波器的两个通带的中心频率分别为350MHz和817MHz。作者给出了一种结构新颖的双模谐振器，该双模谐振器由一个短路枝节和两个开路枝节构成，结构示意如图1（a）所示。谐振器的传输线模型如图1（b）所示。该双模谐振器可以激发两个谐振频率，通过改变短路枝节和开路枝节的物理尺寸来设计这两个谐振频率。

基于传输线理论，该谐振器的输入导纳由下列公式得出^[12]：

式中：θ_n(n=1,2,...,6)表示谐振器对应各部分枝节的电长度。根据（1）~（6）式得出双模谐振器的输入导纳Y_in，由谐振条件Y_in=0得出双模谐振器的谐振频率，再根据传播常数β、谐振器的物理长度L和谐振器电长度θ的等效关系：θ=βL，可以得出各枝节物理尺寸。

                   

(a)                                                                (b)

图1 (a)双模谐振器示意图 (b)双模谐振器传输线模型

基于θ和f之间的数值关系，可以得到f与L之间的数值关系。双模谐振器的谐振频率主要取决于L₁+L₆、L₂、L₃、L₄、L₅。L₁+L₆、L₄、L₅对f₁、f₂都有影响。L₂、L₃主要影响f₂，对f₁影响较小。以L₃、L₅与f₁的关系和L₃与f₂的关系举例说明，通过改变L₃、L₅的物理尺寸可以改变f₁的数值，而f₂的数值不变，如图2（a）所示。通过改变L₃的物理尺寸可以使f₂的数值改变，而f₁的数值不变，如图2（b）所示。

   

(a)                                                                      (b)

图2（a）f₁与L₃、L₅的关系（b）f₂与L₃的关系

根据仿真软件分析双模谐振器的频率响应特性，参考双模谐振器计算的物理尺寸，调节各组成枝节的长度得到双模谐振器频率响应曲线，如图3所示。

图3频率响应曲线图

3  滤波器的设计

3.1 谐振器之间的耦合

在两个谐振器之间存在两条耦合路径，分别是通过S₁之间的耦合和通过S₂之间的耦合，如图4（a）所示。两个谐振器的耦合频率响应曲线如图4（b）所示，每个谐振器激发两个谐振频率。每个通带谐振器间的耦合系数由公式（7）（8）得出：

图5（a）（b）显示了两个通带相邻谐振器的耦合系数和谐振器间距的仿真结果。从图5中可以看出，随着S₁的增大，第一通带和第二通带的耦合系数均减小。随着S₂的增大，第二通带的耦合系数变大，而第一通带的耦合系数基本保持不变。这与前面的结果分析一致，可以独立调整S₁、S₂的大小，使其满足滤波器耦合系数的设计要求，增加了滤波器设计的自由度。

  

(a)                                                                           (b)

图4（a）双模谐振器耦合布局（b）耦合谐振器频率响应曲线图

   

(a)                                                                       (b)

图5（a）耦合系数与S₁的关系（b）耦合系数与S₂的关系

3.2 外部品质因数

在上述分析中已经确定了滤波器的尺寸和耦合系数，接下来需要确定所需要的外部品质因数和对应的馈线位置。每种模式的双模谐振器的外部品质因数由公式（9）确定:

其中f₀为耦合谐振频率，BW_-3dB为耦合曲线-3dB的带宽。滤波器采用弯折T型馈线的耦合方式，如图6所示。两个通带的外部品质因数Q_e1和Q_e2主要和g有关，其关系如图7所示。可以看出，第一通带和第二通带的外部Q_e值随着g值的增大而同时增大。因此，在设计滤波器时，根据滤波器的带宽来确定相应的g值。

图6 外部耦合布局

图7 Q_e与g的关系

3.3 滤波器的仿真结果与分析

该高温超导滤波器是在厚度为0.5mm的MgO基底上的双面DyBa₂Cu₃O₇薄膜上设计，布局如图8所示。该滤波器的整体尺寸为19.65*20mm²。最终优化滤波器的尺寸为：L₁=15.88、L₂=1.02、L₃=5.9、L₄=1.24、L₅=7.22、L₆=4.45、W₁=0.3、W₅₀=0.48、S₁=0.68、S₂=1.42（单位：mm）。

 

图8 双通带高温超导滤波器布局图

通过全波电磁仿真软件对电路进行模拟，结果如图9所示。两个通带的中心频率分别为350MHz和817MHz，对应的相对带宽分别是0.71％和1.93％，回波损耗低于25dB，带外抑制度高于50dB。由于该滤波器外部品质因数的独立设计有局限性，因此在此基础上如何实现外部品质因数的独立设计将是以后的工作重点。表1是本设计的滤波器参数与部分已报道的双通带滤波器参数进行的对比。

 

图9 S参数响应曲线

表1 本工作与其他工作对比

文献	C.F./MHz	FBW/%	RL/dB	S/mm2
[5]	1490/2340	2.69/3.42	18.5/18.1	17.2*14.7
[6]	240/540	16.7/25.92	16.65/17.17	36.65*32
[8]	1500/2400	9.6/12	21/23.5	12.04*7.74
[9]	1800/3500	10月14日	25/28	12.9*10.3
本文	350/817	0.186/0.56	43.31/28.55	19.65*20

注：C.F.为通带的中心频率；FBW为相对带宽；RL为回波损耗；S为滤波器尺寸。

4  结论

设计了一款基于双模谐振器的双通带高温超导滤波器。双模谐振器由一个短路枝节和两个开路枝节构成。通过调整谐振器结构的相应物理参数，完成了滤波器两个通带中心频率及带宽的独立设计，具有较高的设计自由度；采用双模谐振器，与传统单模谐振器的设计方式相比，结构更紧凑，滤波器的物理尺寸更小，为无线通信系统双通带高温超导滤波器的应用提供一种新的设计思路。

参考文献

[1] Lee K C, Su H T, Haldar M K. A review of centrally loaded multimode microstrip resonators for bandpass filter design [J]. AEU-International Journal of Electronics and Communications, 2015, 69(10): 1533-40.

[2] Xiong Y, Zhang W, Zhong Y-P, et al. Dual-tri-band bandpass filters with fully independent and controllable passband based on multipath-embedded resonators [J]. International Journal of Microwave and Wireless Technologies, 2020, 12(10): 1012-9.

[3] Heng Y, Guo X, Cao B, et al. Tri‐band superconducting bandpass filter with high selectivity [J]. Electronics Letters, 2013, 49(10): 658-9.

[4] Heng Y, Guo X, Cao B, et al. Compact superconducting dual‐band bandpass filter by combining bandpass and bandstop filters [J]. Electronics Letters, 2013, 49(19): 1230-2.

[5] MA P, WEI B, HONG J, et al. Coupling Matrix Compression Technique for High-Isolation Dual-Mode Dual-Band Filters [J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(6): 2814-21.

[6] Yu X, Xi W-B, Wu S-T, et al. Design of a dual-wideband high temperature superconducting filter [J]. Physica C: Superconductivity and its Applications, 2021, 589.

[7] Zhou L, Li H, Long Z, et al. Design of High-Temperature Superconducting Dual-Band Filter With Multiple Transmission Zeros [J]. IEEE Transactions on Applied Superconductivity, 2019, 29(6): 1-12.

[8]季来运,马杰,孙钧,王朗,李演奇,刘彬.双通带高温超导滤波器的研制[J].中国科学:信息科学,2011,41(01):121-126.

[9] Gao L, Zhang X Y. High-Selectivity Dual-Band Bandpass Filter Using a Quad-Mode Resonator With Source-Load Coupling [J]. IEEE Microwave and Wireless Components Letters, 2013, 23(9): 474-6.

[10] Haiwen L, Pin W, Yulong Z, et al. Dual-Band Superconducting Bandpass Filter Using Quadruple-Mode Resonator [J]. IEEE Transactions on Applied Superconductivity, 2014, 24(2): 130-3.

[11] Sun S-J, Su T, Deng K, et al. Compact Microstrip Dual-Band Bandpass Filter Using a Novel Stub-Loaded Quad-Mode Resonator [J]. IEEE Microwave and Wireless Components Letters, 2013, 23(9): 465-7.

[12] POZAR D M. 微波工程 [M].第三版. 张肇仪，周乐柱，吴德明，等，译. 北京: 电子工业出版社，2006: 49-55

本文MWRF.NET独家版权所有，未经允许不得转载！