行波管中的混沌现象

一、引言

通常我们在分析有反馈行波管振荡系统的振荡建立过程时，可以利用行波管的输入-输出特性以及反馈系数计算出每次循环后行波管的输出功率。这样的过程可以用下面的离散化的演化方程来描述。

P_out,n=f(P_in,n)，

P_in,n=P_out,n+Fd，

其中，P_out、P_in、Fd以dB计。

显然这是一个非线性系统，这类似于一维抛物线映射。只要关系式f(P_in)满足一定的条件及Fd为合适的值时，这样的反馈系统就可以出现混沌现象。基于上述考虑我们用实验的方法对此反馈系统进行了实验研究。观察到行波管可以工作在三种状态下：单频振荡、分岔及混沌。

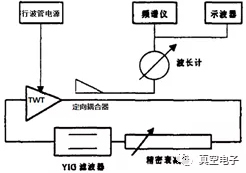
图1、实脸装置简图

二、实验及数据

为了观察行波管中的混沌现象，我们采用了图1所示的实验装置。图1中的行波管为某一储频行波管,此行波管在Uh=2047V,  Ic=4.0mA 下的输入-输出特性曲线如图2所示。由图2可知此管的输入-输出曲线 的后半段随输入功率的增加，输出功率下降较快，符合产生混沌的要求。

图2、某行波管的输入-输出特性曲线

实验观察时，首先使反馈量为最小，然后逐渐增加反馈量,同时在频谱仪上观察行波管的输出结果。在增大反馈量的过程中可以看到：首先为单根谱线，其次是等间隔的多根谱线（两分岔），且谱线的高度由中间向两边逐渐降低，再次在原多根谱线中央出现新的谱线（第1次倍周期分岔），而后几次在原谱线中央出现新的谱线（多次倍周期分岔），最后出现中央高两边低的杂乱谱线（混沌），如图4所示。

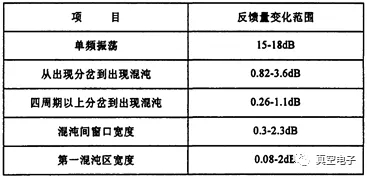
实验时我们在7.9-13.0GHz范围内观察了改变反馈量时，行波管从单频振荡到分岔再到混沌的发展过程。发现只有在9-12.6GHz范围内才能出现混沌。我们在此范围内每隔500MHz进行一次观察。观察结果如表1所示。

表1

在有反馈的情况下,行波管的输出可以计为A(t)cos(ωt)。在N周期分岔时，设幅度分别为A1，A2，…，As，…，AN，作幅度的傅里叶分析结果为:

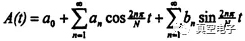
其中

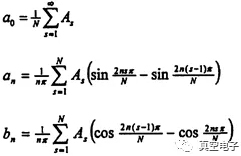
由以上的分析，谱线的间隔与反馈系统的延时有关。实验中改换不同长度的电缆作试验，证实了这一点。实验采用的反馈系统延时为39.0-40.0ns，测得两分岔时，谱线的间隔宽度为12.0-13.0MHz。

以上作傅里叶分析时，未考虑噪声的影响，可得出在两分岔时主谱线与相邻的副谱线间隔应是两相邻的副谱线之间距的一半。而在两分岔时实验中观察到的是，所有的谱线间距是相等的。这是因为实际系统是有噪声的，造成在一个循环周期内行波管的输出不恒定所引起的。

实际系统中用了YIG磁调滤波器，不用此滤波器能不能观察到从分岔到混沌的发展过程呢？回答是能。只是不用滤波器时，能量分布在较宽的频带中，谱线的高度要大幅度的降低，如图3所示。而用此滤波器能起到集中能量的目的，同时控制混沌的中心频率，如图4所示。

实验观察表明，螺旋线电压的微小变化，就可明显影响行波管中的混沌产生。利用此性能，可以在螺旋线上加10伏左右的调制电压对行波管产生的混沌进行调制，从而产生强烈的闪烁效应，这对电子对抗是很有用的。

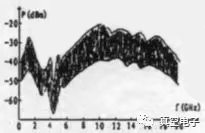
图3、无滤波器时的混沌频谱

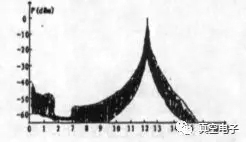
图4、有滤波器时的混沌频谱

三、结束语

行波管中的混沌现象研究开始的较晚，但在海湾战争之后美国及西方各国一直在强化这方面的研究工作。

本文介绍了用实验方法对行波管中的混沌现象进行研究得出的一些结果。这对进一步探索研究行波管中的混沌现象有很大的作用。利用行波管中混沌现象产生的微波噪声，可以制成噪声雷达，提高雷达的抗干扰性，也可以作为电子对抗中干扰机的噪声源，因此对行波管中的混沌现象的进一步研究是有现实意义及应用前景的。