微波笔记·参数提取法设计带通滤波器

有人说微波技术是匹配的艺术，而滤波器又是匹配电路的典型结构，它的理论在微波电路中有重要作用。前辈们花了大量的时间来研究如何准确设计一个滤波器，从拓扑结构的数学综合到结构件的LC等效等产生了很多实用的方法和工具。

大部分的匹配结构都具有带通特性，因此掌握高效带通滤波器的设计方法对微波电路的设计有很大的帮助。我了解到的带通滤波器设计方法有：

· 外部Q值+耦合系数提取+经验调谐优化
· 逐级回波群时延提取耦合系数和谐振频率法
· 逐级回波相位提取耦合系数和谐振频率法
· 参数提取法（通过测试或仿真出的S参数，用特定的拓扑结构提取出对应的耦合矩阵，然后和理想耦合矩阵对比从而设计出理想的滤波器）
· 回波时域响应法

这些方法的核心都是为了简单高效的找出谐振频率和耦合系数，从而准确的实现理论拓扑到实际结构的转换。详细的理论介绍可以参考《通信系统微波滤波器-基础·设计及应用》，王松林译。这篇文章主要介绍参数提取法。逐级回波群时延提取法可参考之前的文章《如何设计一个带通滤波器》。

写这篇文章时我采用了混合方法（回波时延法+参数提取法），逻辑可能会产生跳跃，但仔细理解，我认为会比较好的了解参数提取方法及我的用心。

1、参数提取法简介

参数提取法的核心是任何一个S参数曲线均可以通过一个多项式进行拟合，而多项式又可以通过耦合矩阵表达，这样如果已知仿真或测试所得的S参数曲线，便可以通过线性回归的方法解算出对应的耦合矩阵。这样就提取出了实际滤波器的耦合及谐振频率参数，因此称为参数提取法。知道了实际产品的耦合系数和谐振频率，通过和理想的耦合矩阵进行比对我们就可以将滤波器设计或调谐至理想状态。

参数提取法的详细理论可以参考《通信系统微波滤波器-基础.设计及应用》及该书引用的论文。该方法核心是曲线拟合，所有曲线拟合的方法均可以用来解决此问题（牛顿法，神经网络法，梯度法……），同所有曲线拟合存在问题类似，该方法存在假收敛等问题。比较好的方法是逐级参数提取，这种方法将在后面详细介绍。（个人经验仅供参考：通过逐级时延法+参数提取是精确仿真滤波器的很好方法，这也是为什么本文采用了混合方法的原因）

2、参数提取在滤波器设计中的应用

这里通过一个9阶18900MHz～24100MHz（中心频率：21500MHz；带宽：5200MHz）的交趾滤波器来说明如何应用参数提取法。相关设计文件见：链接：https://pan.baidu.com/s/1nwPnTVj 密码：0rmv

该滤波器理想的9阶切比雪夫耦合矩阵及群时延数据见图1，该excel工具见：链接：https://pan.baidu.com/s/1ggGCD4R 密码：t712

图1、理想的耦合系数及群时延数据

· 本征谐振频率的确定

这里不做过多展开，仿真结果见图2

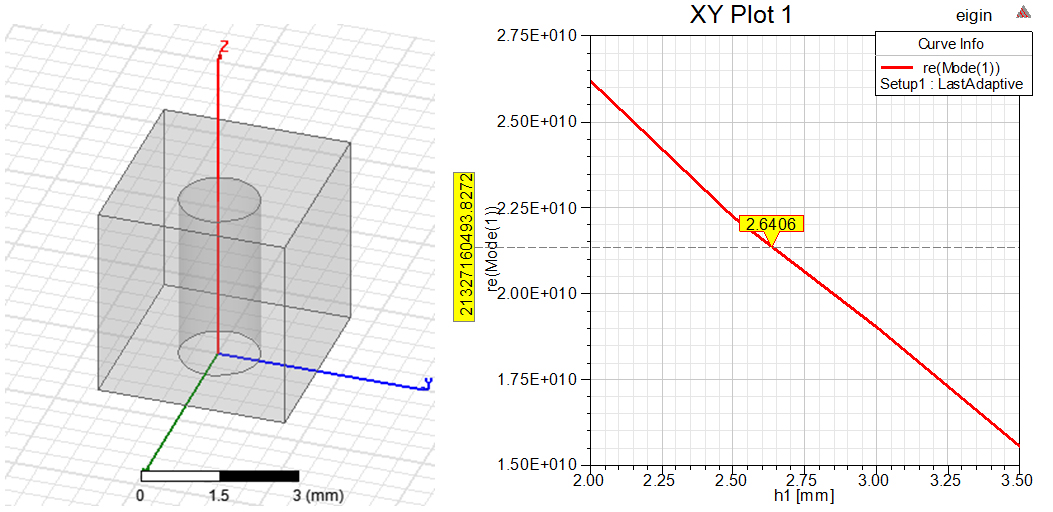
图2、谐振柱本征模式仿真

· 输入耦合确定

输入耦合采用群时延法是比较简便的，这里不做更多展开，直接通过仿真确定参数，通过查图2的结果可以知道输入抽头高度tapin=2.8mm，h1=3.5mm时接近理想输入耦合所需群时延0.1ns。

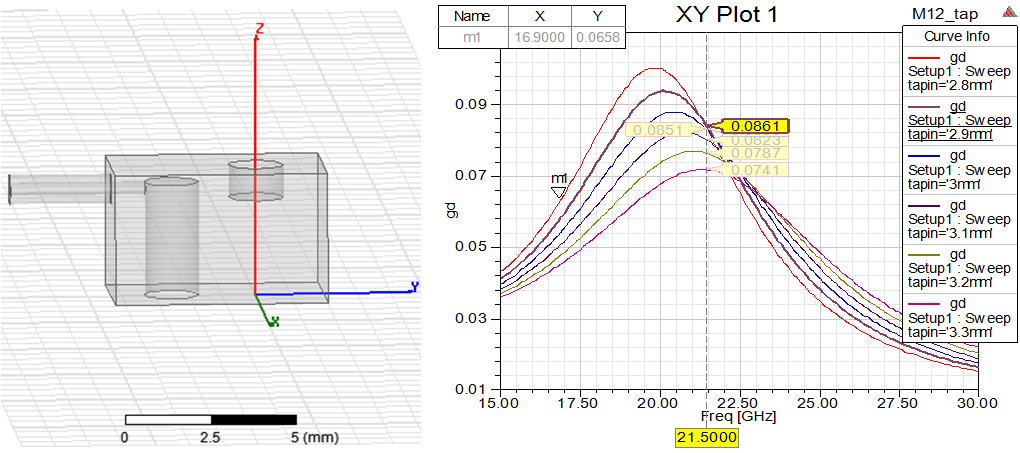
图3、输入耦合的确定

· 12耦合系数及谐振频率确定

个人经验是两个谐振器用群时延法找耦合系数是最实用的方法，但这里采用参数提取法来说明参数提取方法的的实现过程。保持输入耦合确定的参数不变，令第二个谐振器高度为本征模式仿真确定的谐振器高度，h2=2.6mm.仿真获取S11参数，如图4所示。

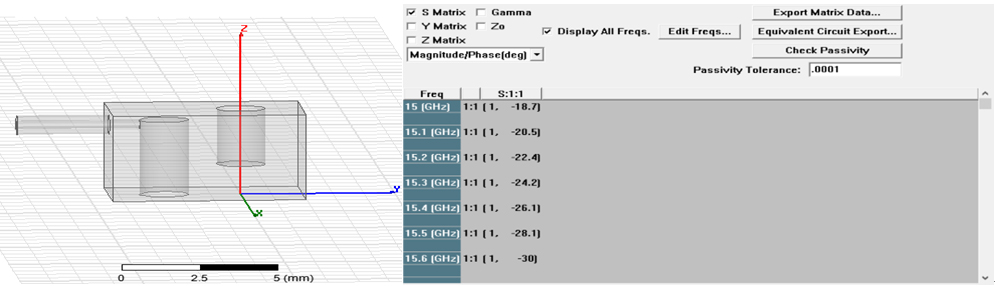
图4、HFSS中获取两个谐振器耦合的S11数据

获得S11数据后，在ADS中建立如图5所示的参数提取模型，模型的核心是使S11严格等于S33，通过ADS优化功能计算得到的参数提取结果和实际数据对比结果见图6所示。

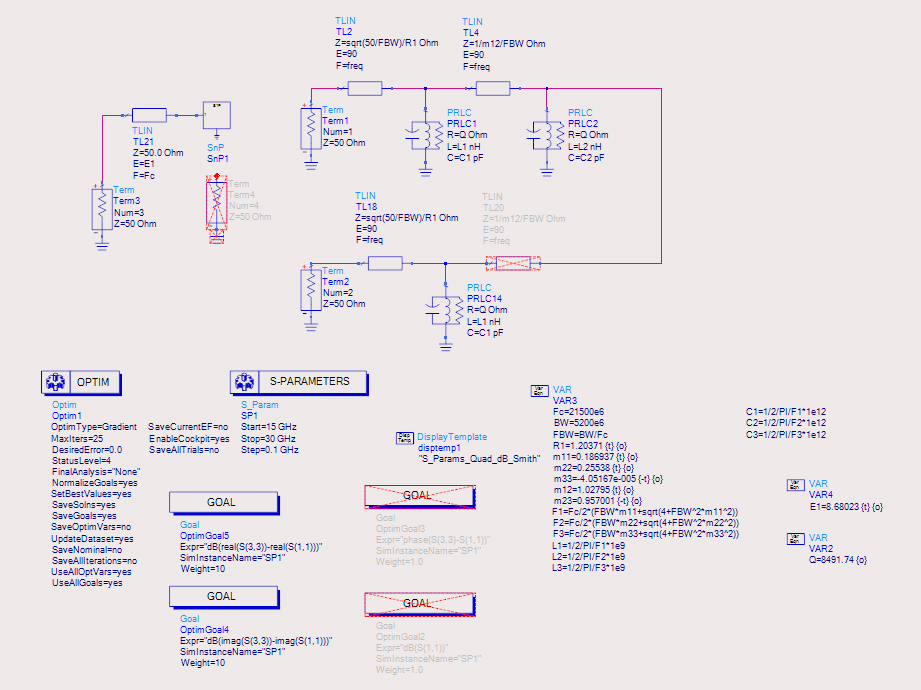
图5、ADS中参数提取模型

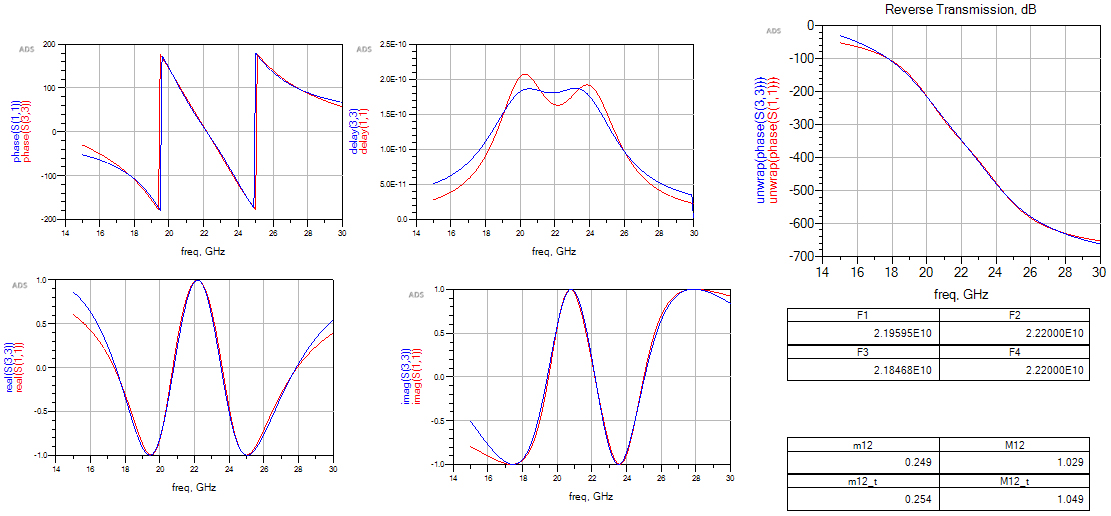
图6、参数提取的拟合曲线和实际曲线对比

通过图6的结果对比可以看出拟合曲线及实际曲线差异非常小，说明提取参数的准确性。图6最后两个表格是通过相位提取法获得的谐振器1和2的谐振频率及耦合系数，通过对比可以发现模拟数据和实际数据吻合的非常好，从侧面印证参数提取的准确性。通过参数提取得到实际模型的耦合矩阵见表1所示。

表1、提取参数和理想参数对比

	F1（MHz）	F2（MHz）	R1	M12
理想数据	21500	21500	1.08	0.9
实际数据	21950	22200	1.2	1.03

通过参数对比对结构尺寸进行调整，进过几次迭代便可以准确找出所需的理想数据，这里不进行详细叙述了。

（个人经验中参数提取最核心的内容就是在ADS中用理想的耦合矩阵提取模型同实际数据进行对比，利用ADS的优化控件实现参数的提取，避免个人编写复杂的数学代码。）

· 3个谐振器耦合系数及谐振频率确定

获得理想的2个谐振器的参数后，建立3个谐振器模型，重复上面的步骤获取3个谐振器的理想结构参数，这里不进行过多叙述，请自行感受。通过上述步骤重复，可以获取3D模型电磁仿真的初始的结构参数见表2或附件的仿真模型

表2、初始3D仿真模型核心尺寸

	Tapin	Ls12	Ls23	Ls34	Ls45	H1	H2	H3	H4	H5
尺寸	2.8	2.5	2.9	3.1	3.1	3.5	2.6	2.6	2.6	2.6

· 参数提取在滤波器整体仿真中的应用

根据表2获取的初始模型尺寸，建立整体模型仿真，获取初始模型的S参数数据用于参数提取。模型及ADS中参数提取的原理图见图7所示，通过ADS中的调谐操作让模型曲线和实际曲线大致接近（曲线拟合的初值很重要），然后通过优化控件对模型进行优化提取耦合系数。

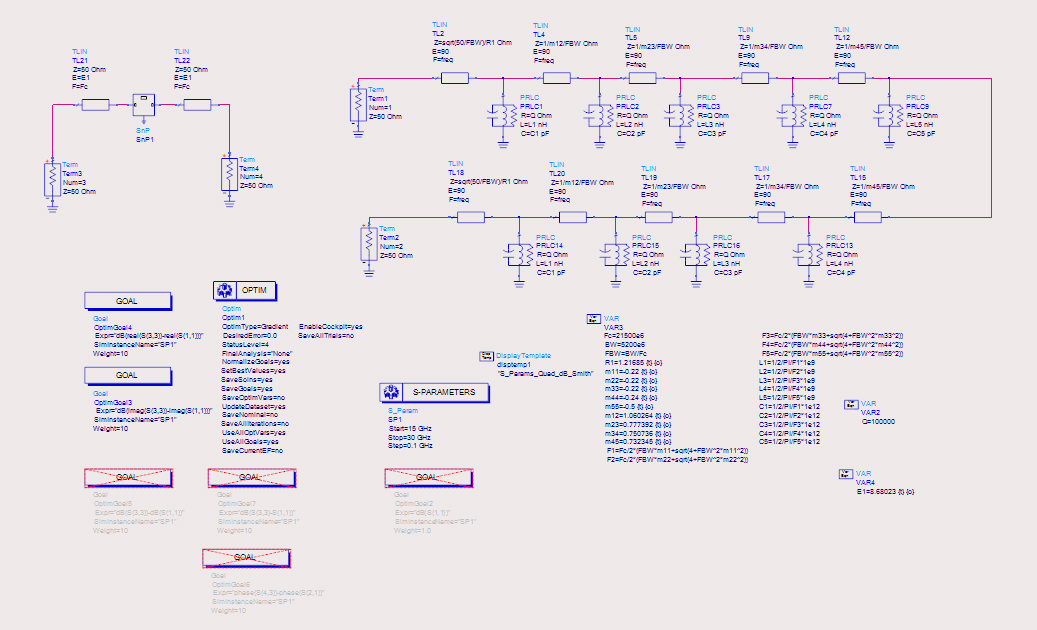
图7、整体仿真模型及参数提取原理图

通过优化，获得的参数提取曲线和实际曲线对比见图8，通过对比可以发现参数提取曲线和实际曲线吻合度非常高。提取参数和理想参数对比见表3。

表3、提取参数和理想参数对比

n	R1	m12	m23	m34	m45	m11	m22	m33	m44	m55
理想数据	1.08	0.9	0.61	0.56	0.55	0	0	0	0	0
实际数据	1.11	1.15	0.84	0.73	0.74	-0.48	-0.05	-0.27	-0.32	-0.33

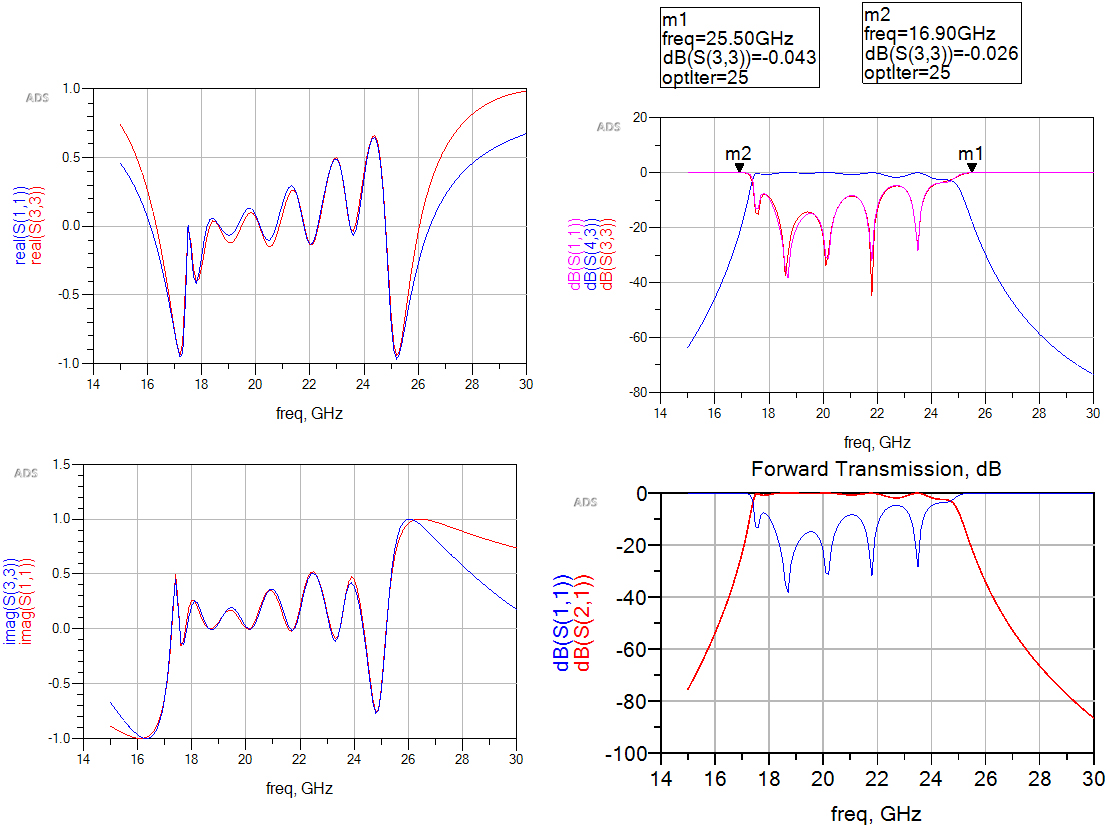
图8、参数提取曲线和实际曲线对比

通过提取的参数和理想参数进行对比，可以判断出各关键尺寸的调谐方向，经过几次迭代后就可以准确设计出滤波器了。通过表3提取的数据可以判断谐振器1/3/4/5谐振频率偏低，m12/m23/m34/m45耦合偏大，根据经验对这些尺寸进行微调进行第二次仿真，仿真结果及参数提取结果见图9所示。

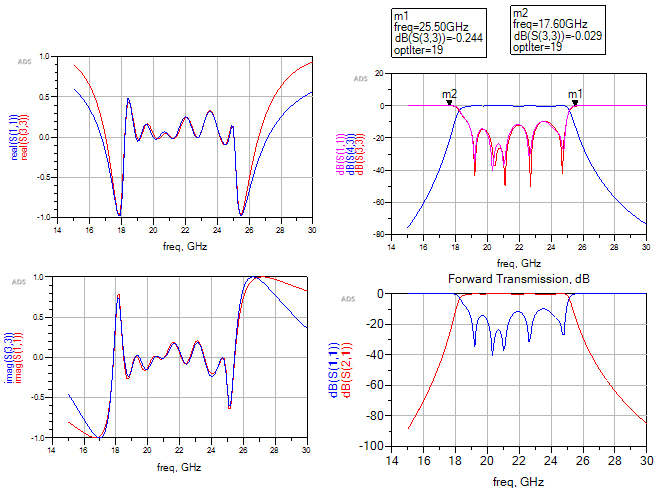
n	R1	m12	m23	m34	m45	m11	m22	m33	m44	m55
理想数据	1.08	0.9	0.61	0.56	0.55	0	0	0	0	0
第一次拟合	1.11	1.15	0.84	0.73	0.74	-0.48	-0.05	-0.27	-0.32	-0.33
第二次拟合	1.12	1.13	0.78	0.68	0.68	-0.06	-0.06	-0.11	0	0

图9、第二次参数提取结果及数据对比

通过第二次拟合发现结果更加接近理想值了，就这样通过多次的迭代就可以设计出完美的滤波器了。

作者：赵强 微信号：q_zhao_ls

简介：
2004～2011 华中科技大学 微电子学与固体电子学 硕士
2011～2015 中电29所西科微波通讯有限公司
2015~ 2018 华为技术有限公司
2018～至今 航天微电科技有限公司成都分公司

本文为MWRF.NET原创文章，未经允许不得转载，如需转载请联系market#mwrf.net(#换成@)