由于微波频段存在趋肤效应,导致微波器件导体内的电流通常集中在表面微米级的厚度内,这是大家所熟知的概念。依据这一原理,业界通常采用下述方法来改善微波器件的损耗,同时降低器件成本:在导体表面(比如铝合金)沉积厚度约为数个趋肤深度的良导体层(比如镀金、镀银)。这一原理也同样应用在改善微波无源器件的无源互调性能方面:低互调器件通常采用镀银表面。
为了衡量导体材料的损耗性能,人们定义了表面电阻R的概念:

换句话说,表面电阻反比于电导率与趋肤深度之乘积。依据这一概念,可以方便地对器件损耗进行评估。以矩形波导为例,如果只考虑矩形波导宽边的损耗,则在工作于基模TE10的条件下,波导传输线的损耗可以按下式计算:
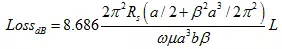
相位常数的计算方法:
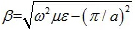
对于趋肤深度的形象理解是:由于电磁波在良导体内部呈现指数衰减,当电磁波渗入导体内部一个趋肤深度的厚度时,电磁波幅度将衰减1/e,也就是36.8%。如果导体厚度达到三个趋肤深度及以上,通常就认为电磁波幅度衰减为零。
以上是我们对于导体损耗与趋肤深度关系的通常认识,下面本文要讨论的问题是:如果良导体的厚度等于趋肤深度甚至小于趋肤深度,电磁波会穿透良导体吗?上面提到的“表面电阻等于电导率与趋肤深度乘积之倒数”该如何应用于导体厚度小于趋肤深度的情形?
实际上,教科书中有关趋肤深度的讨论是针对导体厚度无限大的理想模型来进行的。当导体厚度等于趋肤深度甚至远小于趋肤深度而演变为导电薄膜时,电磁波渗入导体内部以后,将在出射导体薄膜时由于导体薄膜阻抗与空气阻抗的失配而发生发射(假设导电薄膜背面为空气介质)。因此,即便导电薄膜的厚度只有一个趋肤深度,此时电磁波的衰减量也不再是上文中所说的36.8%。
依据A E Kaplan的论文《on the reflectivity of metallic films at microwave and radio frequencies》,在自由空间中,电磁波垂直入射导电薄膜时,其功率透射系数可按下式计算:
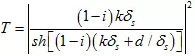
下图给出了依据该理论得到的金属铝厚度对电磁波衰减量的影响规律(电导率为38.6 MS/m,频率为10 GHz)。
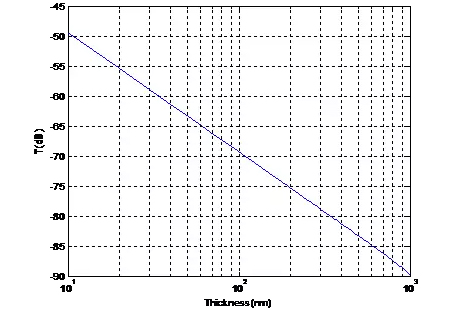
图1、导电薄膜对电磁波的衰减
由上图可见,即便铝膜厚度只有10 nm,其对10 GHz电磁波的衰减也可以达到50 dB,远大于我们通常从趋肤深度角度所理解的衰减量。
实际上,对于导电薄膜的情形,表面电阻可表示为:

亦即,假设矩形波导的壁厚小于趋肤深度,则计算其导体损耗时,需要将教科书中表面电阻公式中的趋肤深度替换为薄膜厚度。下面,我们给出HFSS的仿真结果,并与理论计算结果对比。电磁波形如图2所示,类似地,这里仅考虑波导宽边的损耗。仿真结果如图3所示(图中loss项表示辐射损耗;黑色线对应左侧纵坐标,红色线对应右侧纵坐标):当电导率为0.5 MS/m时,辐射损耗显著,且随膜厚增加而减小;而当电导率为30 MS/m时,辐射损耗明显降低。
图2、宽边为导电薄膜的矩形波导模型
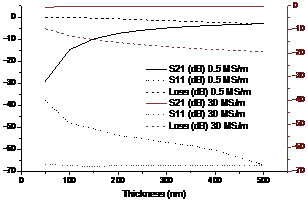
图3、电导率及膜厚对矩形波导S参数及辐射损耗的影响仿真结果
图4给出了HFSS仿真与理论计算结果的对比:采用电导率与膜厚定义的表面电阻得到的理论计算结果与HFSS仿真结果吻合良好,表明针对导电薄膜的情形,其表面电阻应为电导率与膜厚乘积的倒数。
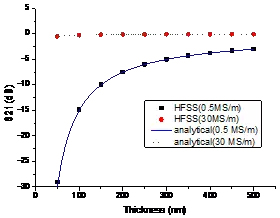
图4、HFSS仿真与理论计算的对比
主要结论:如果良导体的厚度等于趋肤深度甚至小于趋肤深度,电磁波仍然会穿透良导体,但是远小于我们通常从趋肤深度角度所理解的衰减量;“表面电阻等于电导率与趋肤深度乘积之倒数”对于导电薄膜的情形,应当替换为“表面电阻等于电导率与膜厚乘积之倒数”。

 粤公网安备 44030902003195号
粤公网安备 44030902003195号