无线电科学与技术中的因子4

摘要：作者早就注意到数字4是无线电科学与技术中一个重要的因子。许多天线、无线电波传播、射频电路与系统常用计算公式中都有它的身影，现罗列如下，供大家学习参考。

正文：无线电科学的基础是麦克斯伟方程。无线电技术的起源是赫兹的工作。赫兹不仅仅证明了麦克斯伟方程所预测的电磁波之存在，也开发了最早的天线，是天线界的鼻祖。马格尼的贡献在于改进与组装，资助与开发了一系列无线电报系统，并在商业上取得成功。

一．天线

天线使无线通信与探测成为可能。因子4在天线基本性能指标定义及设计中发挥着重要作用。

1. 天线方向性系数

天线方向性系数D 可以按照如下公式计算：

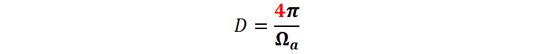(1)

公式(1)中Ω_α 是天线波束的立体角。据此定义，天线方向性系数是大于或等于1的无量纲的量。

2. 天线散射口径

天线散射口径A_s 是天线最大有效口径A_em 的4倍。

(2)

3. 天线噪声

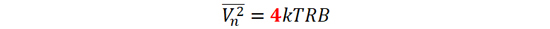(3)

公式(3)中k 是玻尔兹曼常数，T 天线噪声温度，R 是辐射电阻，B 是频带宽度。

4. 单极子天线

马格尼将“有线电”中的接地慨念，引入到无线电中，发明了单极子(monopole)天线^[1]。单极子天线工作长度 l 可以按照如下公式选取：

(4)

公式(4)中λ 是工作波长。

5. 短路微带天线

短路微带天线保持了传统微带天线低剖面、易集成等优点，同时还具有谐振尺寸更小及主辐射面波束宽度大致相等的优点。短路微带天线谐振尺寸可以按照如下公式选取：

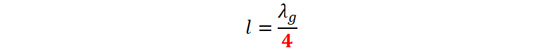(5)

公式(5)中λ_g 是介质波长。但是，为什么短路微带天线没能得到很好的应用？究其原因主要是交叉极化辐射非常严重^[2]。

微带天线的基本理论是腔模理论。后人在腔模理论的基础上发展出了寄生模及多模设计方法来进行微带天线设计。作者认为这些后续发展起来的设计方法存在着先天的缺陷。虽然基于这些方法所设计的微带天线，一些指标确实改善了，但同时又恶化了微带天线其它指标。作者还是非常推崇腔模理论中的主模工作原理，发展出主模耦合理论及设计方法。基于主模耦合理论所设计的微带天线几乎改善了微带天线的所有性能指标，而且还同时可以实现天线小型化^[3-5]。沿着这一学术思想，我们完美地解决了困扰了微带天线界近半个世纪的短路微带天线交叉极化辐射非常严重的难题。改良式短路微带天线H面交叉极化电平可以表示为：

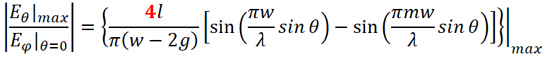(6)

公式(6)中w 是辐射片宽度，g 是耦合缝隙宽度，θ 是俯仰角，m 的取值主要影响天线的交叉极化方向图而基本不改变天线的主极化方向图。当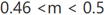时，交叉极化辐射从单个零点变成三个零点。

6. 折叠半波偶极子天线

设半波偶极子天线辐射电阻为R_d 欧姆, 折叠半波偶极子天线辐射电阻R_fd 可以按照如下公式计算：

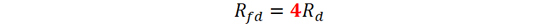(7)

7. 布克关系（Booker’s Relation）

亨利•乔治•布克(H. G. Booker) 将光学中的巴比涅原理推广到电磁场^[6]，并以此发现了互补天线阻抗之间存在如下关系：

(8)

公式(8)中Z_s 是缝隙天线阻抗，Z_d 是缝隙天线之互补天线的阻抗，Z₀ = 377欧姆是自由空间的波阻抗。布克关系告诉我们：如果缝隙天线阻抗已知，它的互补天线的阻抗也就知道了。

8. 德尚关系（Deschamps's Relation）

乔治•德尚（G.A. Deschamps）将布克关系扩展到了多端口天线^[7]。对于两端口互补天线，德尚关系可以表达如下：

(9)

公式(9)中Z₁₁ 与Z₂₂ 分别是一端口与二端口自阻抗，Z₁₂ 是一端口与二端口之间互阻抗。

9. 输入阻抗关系（Input Impedance Relation）

为了顺应系统级集成的潮流，促进天线与电路协同设计的发展，作者正在努力统一天线与电路之间的一些术语，增进天线与电路工作者之间相互了解，尽量减小因术语差异而造成的误解。作者从定义差分与单端口天线入手，引入了天线的差分输入阻抗Z_dif ，共模输入阻抗 Z_com ，单端口输入阻抗Z_sig ，并发现了它们在谐振天线之间的如下关系：

(10)

 

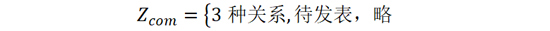(11)

公式(10)与（11）中Z_s 是端口自阻抗，Z_m 是端口之间互阻抗。上述关系对集成无线系统中天线与电路协同设计有着重要的理论指导意义^[8]。

二．无线电波传播

无线电波传播在不同传播区域遵循不同传播规律。因子4在确定传播区域及表征传播规律中起着重要作用。

10. 地平面上视距传播拐点位置

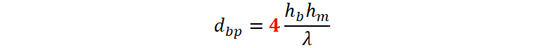(12)

公式(12)中h_b 是基站天线高度，h_m 是移动台天线高度，λ 是工作波长。

11. 地平面上视距传播拐点后路径衰减指数

在地平面上视距传播拐点位置之前，传播区域属于第一菲涅耳净空区，路径损耗可以使用自由空间公式计算。在地平面上视距传播拐点位置之后，路径损耗可以使用如下公式计算：

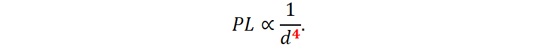(13)

如果读者想知道诸如隧道等限定空间中视距传播拐点位置如何确定及路径损耗如何计算？请参阅作者2003年发表的有关无线电波传播的文章^[9]。

三．无线电系统

无线系统中的有源器件、无源零件、电路、阻抗变换都会遇到因子4。

12. 约翰逊-奈奎斯特噪声

该噪声又称热噪声，它是平衡状态下电导体内部电荷载流子（通常是电子）的热搅动产生的电子噪声，无论施加何种电压，都会发生这种噪声。

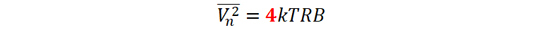(14)

公式(14)中k 是玻尔兹曼常数，T 是电导体的温度，R 是电导体的电阻，B 是频带宽度。

13. 场效应晶体管沟道噪声

(15)

公式(15)中γ 是经验数，与沟道长度有关，由实验来定；g_m 是沟道电导。

14. 阻抗变换器

当传输线长度为λ/4 ，输入阻抗Z_i 与负载阻抗Z_l 之乘积等于传输线特征阻抗Z_c 的平方。

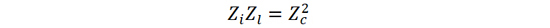(16)

15. 非线性增益压缩

当输入信号幅度A 增加时，所有电路或系统的增益都会受到因非线性所带来的压缩。如下公式（16）中a₁ 是电路或系统一阶线性系数，a₃ 是三阶非线性系数，a₃ 为负数 ^[10]。

(17)

16. 三阶截取点

当输入信号幅度A 增加到A_IP3 时，电路或系统的输出信号中三阶交调分量与一阶线性分量相等。A_IP3 可以由如下公式计算 ^[10]：

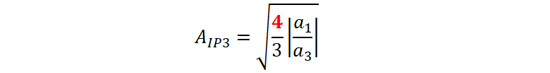(18)

结论：数字4作为无线电科学与技术中的一个重要因子，作者认为其主要原因有：莫里茨•赫尔曼•冯•雅哥比（Moritz Hermann von Jacobi）定理所决定的最大功率传输条件所要求；球体的立体角；三角函数计算等。此外，作者相信上述罗列肯定不完整，欢迎大家补充。最后，有感于上面简单明了的公式，让我用一句名言“简洁即精致 （Simplest is the utmost sophistication）”来结束此文。

参考文献:

[1] US patent 586193, Guglielmo Marconi, Transmitting electrical signals, filed December 7, 1896, granted July 13, 1897.
[2] E. Penard, J. P. Daniel, “Open and hybrid microstrip antennas,” IEE Proc. Pt. H, vol. 131, no. 1, pp. 38-44, Feb. 1984.
[3] Z. Shao, Y. P. Zhang, “Differential shorted patch Antennas,” IEEE Trans. Antennas Propag. vol. 67, no. 7, pp. 4438-4444, Jul. 2019.
[4] Z. Shao, Y. P. Zhang, “Cross-polarization reduction of shorted patch antenna by coupled TM01 mode,” to appear in IEEE Trans. Antennas Propag.
[5] Z. Shao, Y. P. Zhang, “Coupled shorted patch antennas with both broadside and conical radiation patterns,” to appear in IEEE Trans. Antennas Propag.
[6] H. G. Booker, “Slot aerials and their relations to complementary wire aerials,” JIEE (London), vol. 93, pt. IIIA, no. 4, pp. 620-626, 1946.
[7] G. A. Deschamps, “Impedance properties of complementary multiterminal planar structures,” IRE Trans. Antennas Propag., pp. 371-378, Dec. 1959.
[8] Y. P. Zhang, “Impedance relations for differential antennas and single-ended counterparts,” submitted to IEEE Trans. Antennas Propag.
[9] Y. P. Zhang, “Novel model for path loss prediction in tunnels,” IEEE Trans. Vehicular. Tech. vol. 52, no. 5, pp. 1308-1314, Sep. 2003.
[10] Y. P. Zhang, Lecture Notes on Radio-Frequency Integrated Systems Design, NTU, Singapore 

作者简介: 张跃平，男，山西省万荣县西村人，博士，教授，无线电电子学家，IEEE Fellow，IEEE天线与传播学会杰出讲师，IEEE天线与传播学会谢昆诺夫论文奖与克劳斯天线奖得主。