随着家庭、建筑和工业应用走向无线化,短距无线装置正成为众人关注的焦点。这些应用通常采用专属或以标准为基础的做法,例如900MHz和2.4GHz ISM(工业,科学和医疗)频带的ZigBee。由于短距无线装置日益流行,终端系统设计人员也须深入了解无线通讯的传输距离。本文讨论无线讯号传播,并建立模型来估算短距无线装置在室内环境的路径损耗及传输距离。设计人员可利用这些模型初步估算无线通讯系统的效能。
在探讨距离估算公式前,设计人员必须了解无线信道和讯号传播环境。无线电信道是发射机与目标接收机之间的传输路径,它具有随机和时变特性,故很难建立模型,这与固定和可预测的有线通道极为不同。因此,设计人员必须使用统计模型来分析这些随机通道。
无线电波传播模型传统的重点是预测发射机外特定距离的平均接收讯号强度,以及某个位置附近的讯号强度变化。无论发射机与接收机的距离为何,大尺度传播模型都能预测其平均讯号强度,这对估算发射机的传送距离很有用。相形之下,小尺度或衰落模型则能分析接收讯号强度在数个波长距离内的快速变化。本文主要讨论大尺度传播模型,它能用来估算无线传输距离。
当发射机与接收机之间没有任何阻碍,并能直接看到对方时,就能利用自由空间传播模型来预测接收讯号强度。自由空间传播模型预测接收讯号强度会随着发射机与接收机之间距离的n次方而衰减,这个函数关系又称为幂次法则函数。当接收机天线与发射机天线之间有段距离时,它所接收的自由空间功率是由下列Friis自由空间方程式决定:

其中PT是发射功率;PR(d) 是接收功率,也是发射机与接收机距离d的函数;GT是发射机天线增益;GR是接收机天线增益;d是发射机与接收机的距离,单位为公尺;λ则是波长,单位也是公尺。
Friis自由空间方程式显示接收功率随着发射机与接收机距离的平方而减少;换言之,接收功率将随着距离增加而以20dB/decade的速率下降。
路径损耗对估算无线传输距离很重要,它等于发射功率与接收功率的相差值(以分贝为单位),代表讯号的衰减程度。从方程式(1)可导出路径损耗等于发射功率除以接收功率,方程式(2)将路径损耗定义为:
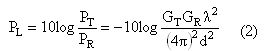
其中PL是路径损耗。假设发射与接收天线都是单位增益,则方程式(2)可简化为:
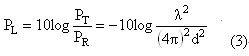


其中d是距离,单位公尺。
只有当d值在发射天线远场时,Friis自由空间公式才能估算接收功率强度。发射天线的远场又称为Fraunhofer区域,是指天线远场距离dF以外的区域。天线的dF等于2D2/λ,其中D是天线的最大实体线性尺寸;另外dF还必须大于D,而且要在远场区内。这个路径损耗公式仅适用于发射机与接收机在对方视线内的理想系统,而且只应用于初步估算。
传播模型把近程距离(close-in distance) d0当成接收功率参考点,设计人员必须利用该参考点的接收功率PR(d0) 计算距离大于d0时的接收功率。设计人员可以利用方程式1和4预测PR(d0),或是测量发射机附近许多点的接收功率,再把它们的平均值当成PR(d0)。设计人员选择近程参考点时,必须确定远场区在近程距离之外。
设计人员可利用这项信息和下列公式计算任何距离的接收功率: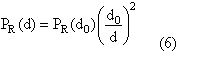
900MHz和2.4GHz频带的短距无线装置设计人员须能根据公式了解那些参数会影响及如何影响传输距离,并将这些参数运用在公式中,以便透过统计方法计算室内和户外环境的路径损耗及传输距离。
随着家庭、建筑和工业应用走向无线化,短距无线装置正成为众人关注的焦点。这些应用通常采用专属或以标准为基础的做法,例如900MHz和2.4GHz ISM(工业,科学和医疗)频带的ZigBee。由于短距无线装置日益流行,终端系统设计人员也须深入了解无线通讯的传输距离。本文讨论无线讯号传播,并建立模型来估算短距无线装置在室内环境的路径损耗及传输距离。设计人员可利用这些模型初步估算无线通讯系统的效能。
在探讨距离估算公式前,设计人员必须了解无线信道和讯号传播环境。无线电信道是发射机与目标接收机之间的传输路径,它具有随机和时变特性,故很难建立模型,这与固定和可预测的有线通道极为不同。因此,设计人员必须使用统计模型来分析这些随机通道。
无线电波传播模型传统的重点是预测发射机外特定距离的平均接收讯号强度,以及某个位置附近的讯号强度变化。无论发射机与接收机的距离为何,大尺度传播模型都能预测其平均讯号强度,这对估算发射机的传送距离很有用。相形之下,小尺度或衰落模型则能分析接收讯号强度在数个波长距离内的快速变化。本文主要讨论大尺度传播模型,它能用来估算无线传输距离。
当发射机与接收机之间没有任何阻碍,并能直接看到对方时,就能利用自由空间传播模型来预测接收讯号强度。自由空间传播模型预测接收讯号强度会随着发射机与接收机之间距离的n次方而衰减,这个函数关系又称为幂次法则函数。当接收机天线与发射机天线之间有段距离时,它所接收的自由空间功率是由下列Friis自由空间方程式决定:

其中PT是发射功率;PR(d) 是接收功率,也是发射机与接收机距离d的函数;GT是发射机天线增益;GR是接收机天线增益;d是发射机与接收机的距离,单位为公尺;λ则是波长,单位也是公尺。
Friis自由空间方程式显示接收功率随着发射机与接收机距离的平方而减少;换言之,接收功率将随着距离增加而以20dB/decade的速率下降。
路径损耗对估算无线传输距离很重要,它等于发射功率与接收功率的相差值(以分贝为单位),代表讯号的衰减程度。从方程式(1)可导出路径损耗等于发射功率除以接收功率,方程式(2)将路径损耗定义为:
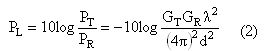
其中PL是路径损耗。假设发射与接收天线都是单位增益,则方程式(2)可简化为:
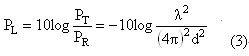


其中d是距离,单位公尺。
只有当d值在发射天线远场时,Friis自由空间公式才能估算接收功率强度。发射天线的远场又称为Fraunhofer区域,是指天线远场距离dF以外的区域。天线的dF等于2D2/λ,其中D是天线的最大实体线性尺寸;另外dF还必须大于D,而且要在远场区内。这个路径损耗公式仅适用于发射机与接收机在对方视线内的理想系统,而且只应用于初步估算。
传播模型把近程距离(close-in distance) d0当成接收功率参考点,设计人员必须利用该参考点的接收功率PR(d0) 计算距离大于d0时的接收功率。设计人员可以利用方程式1和4预测PR(d0),或是测量发射机附近许多点的接收功率,再把它们的平均值当成PR(d0)。设计人员选择近程参考点时,必须确定远场区在近程距离之外。
设计人员可利用这项信息和下列公式计算任何距离的接收功率: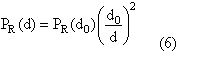
对于在1-2GHz范围操作的实际系统,室内环境的参考距离是1公尺,户外环境则为100公尺。
常用的射频功率强度单位是毫瓦分贝或瓦分贝,而不是绝对功率强度。因此方程式(6)可表示为:
下例说明这些观念。假设发射频率900MHz,发射功率6.3mW (8dBm),并且使用单位增益的发射和接收天线,则在户外视线范围1200公尺处的接收功率可计算如下:户外环境的参考距离为100公尺,900MHz讯号的波长为0.33公尺,因此可先利用方程式(1)的值计算100公尺处的接收功率如下:
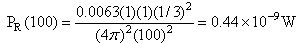


利用方程式(7)可得到1200公尺处的接收功率为:

以及:

您还可利用方程式(5)验证接收功率就是这个值。
故在没有障碍物且视线可及的理想环境里,当发射功率为8dBm时,距离1200公尺位置的接收功率约为-85dBm。当然,实际环境下的接收功率会低于该理想值,因为目标点与发射机之间可能有障碍物,或根本就在视线外。从前述例子得知路径损耗为PT – PR,因此它等于8dBm – (-85dBm) = 93dB。
实际路径损耗公式
任何实用的无线传感器系统都必须知道其最大可靠传输距离。这个无线系统传输距离直接由链路预算参数决定:

其中LB是以分贝表示的链路预算,PT是以毫瓦或瓦分贝表示的发射功率,GT是以分贝表示的发射机天线增益,GR是以分贝表示的接收机天线增益,RS是接收机灵敏度,代表系统能够侦测并提供适当讯号杂波比的最小射频讯号。接收机灵敏度如方程式14所示:

其中-174dBm/Hz是热噪声基准,NF是以分贝表示的接收机总噪声指数,B是接收机总频宽,SNRMIN则是最小讯号杂波比。如果发射机与目标接收机之间的总路径损耗大于链路预算,数据就会遗失,通讯也无法进行。因此,设计人员在发展最终系统时必须精确分析路径损耗特性,并与链路预算比较以获得初步的距离估算值。
室内信道路径损耗
室内无线电信道不同于户外信道,这是因为室内通道的传输距离较短,通道损耗的变动也较大,所以接收讯号强度的变化较大。但对固定无线装置而言,这个部分却可忽略不计。建筑物的平面配置、类型和建筑材料都会对室内讯号传播产生很大影响。研究人员将室内通道分为两种,一种视线可及的信道,另一种是受到不同程度阻隔的通道(参考文献1)。建筑物的内部与外部结构可能含有许多不同的隔间和障碍物,隔间方式取决于该建筑是在家庭或办公室环境。建筑结构的隔间是固定隔间,活动隔间则能到处移动,而且隔间顶端不会碰到天花板。家庭通常采用木板隔间,办公室建筑则会在楼层之间使用钢筋混凝土,并且采用活动隔间方式。
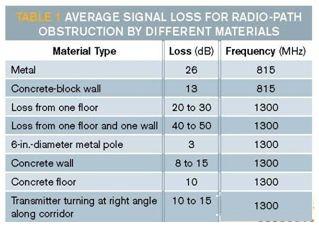
建筑物有许多不同的隔间方式,它们的实体和电气特性也差异很大,很难靠着通用模型来分析室内信道。但经由广泛的研究,业界已将常用材料的讯号损耗制成表格(表1)。

方程式(15)是利用对数距离路径损耗模型所得到的室内信道实际路径损耗模型:

其中X是以分贝为单位的零平均值高斯随机变量,σ则是标准差。如果为固定装置,则可将Xσ的影响忽略不计。利用方程式(4)计算1公尺距离的路径损耗值,再将结果代入方程式15即可得到:


建筑物内的传播模型包含建筑物类型和障碍物的影响。此模型不但有弹性,还能将路径损耗测量值与预测值间的标准差减到4dB左右,胜过仅使用对数距离模型时的13dB。方程式17代表衰减因子模型:

其中nSF代表同楼层测量时的路径损耗指数,FAF则是楼层衰减因子 (表3),设计人员可根据表2决定楼层衰减因子。下面的例子示范如何使用前述表格及方程式,它利用下式计算915MHz和2.4GHz讯号在户外空旷环境中1200公尺距离的路径损耗:

从上式可得到915MHz的路径损耗为:
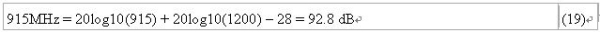
2400MHz的路径损耗则为:
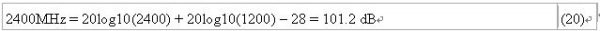
传输讯号的频率越高,路径损耗就越大,这会缩短高频讯号的无线传输距离。例如在户外空旷环境里,2.4GHz无线装置就比915MHz装置多出大约8.4dB的路径损耗。
另一个例子则是以同一层楼和三个楼层的固定隔间办公室环境为对象,利用表2的数据来计算915MHz和2.4GHz讯号在100公尺距离的路径损耗。从表3可知同楼层的平均路径损耗为3dBm,把这个n = 3的值代入下式:

其中σ=14dB。
从表2可算出三层楼传播的楼层衰减因子约24dB,标准差则为5.6dB。把这项信息代入下式:

其中σ = 5.9dB。
第三个例子则假设系统使用单位增益发射与接收天线、发射功率为8dBm、以及接收机灵敏度为-100dBm,然后估算915MHz讯号在前两个例子里的传输距离。注意此时的系统链路预算为8 – (-100) = 108dB。
为了说明路径损耗公式里的标准差,链路预算最好预留10dB左右的边限。这表示可供使用的链路预算为98dB,超过了第一个例子92.8dB路径损耗;因此,设计人员可将系统的户外传输距离视为1200公尺。在室内环境里,路径损耗为91.2dB,预留10dB边限时的可用链路预算约为98dB,这同样超过路径损耗。因此,设计人员可将系统的室内传输距离视为100公尺。
[参考文献]
Rappaport, Theodore S, Wireless Communications Principles and Practice, Prentice Hall, 2001.

 粤公网安备 44030902003195号
粤公网安备 44030902003195号