自从我学会了如何从右端握住电烙铁后,与射频相伴的工作便成了我的酷爱。数字化电磁学(EM)已经吸引了我过去二十年的注意力。渐渐地,我开始了以“在过去的好时光”的方式来回味麦克斯韦方程。我开始对麦克斯韦这个家伙产生了兴趣(图1)。历史学家们公认他是19 世纪最出色的物理学家,与爱因斯坦(Einstein)和牛顿(Newton)齐名。任何一个书店或图书馆都有爱因斯坦和牛顿的传记…那么麦克斯韦的传记又在哪里呢?

图 1 詹姆斯·克拉克·麦克斯韦创建了电磁场理论,并且被认为与牛顿和爱因斯坦齐名。
确实,很难找到麦克斯韦的传记。在过去大约十年中,我做了很多努力找到了一些,并且在管理公司,编程,写文章和做研究之余,我已经决心要了解一点我们领域的这位创始人。虽然无论从哪方面讲我都算不上是一个历史学家,但我愿意与你们分享从一个微波工程师的视角出发所得到的一个体会。为此我所取得的一个成就便是作为一个MTT-S 杰出演讲人无偿地来讲述“詹姆斯·克拉克·麦克斯韦的一生” [1] 。在这篇文章中,我花费了比演讲所允许的更多的时间详细地讨论了影响麦克斯韦最重要的遗产的事件。有趣的是,他最重要的遗产并不是位移电流。甚至不是麦克斯韦方程。
了解麦克斯韦一生最好的信息来源可能是刘易斯·坎培尔(Lewis Campell)和威廉·加内特(William Garnett)所写的1882 年的传记[2]。图2 是来自于传记的根据现实场景所绘制的水彩画。这幅画展示出当麦克斯韦还是个孩子时便对波现象(小提琴)产生了兴趣。通常,这本书只能在大图书馆的稀有图书室中才能找到。我们还是回到当我第一次对麦克斯韦产生兴趣时,我得到了一本这样的书,我对它进行了扫描,再转为文字形式,这是一个相当长的处理过程。今天,你可以从[3]所列出的网址上免费下载PDF 格式的完整的传记,包括第二版中的特别部分。

图 2 在麦克斯韦六岁时,他便对小提琴是如何工作的产生了兴趣,完全忽略了舞蹈者。这幅画是取自描述生活情景的水彩画。
坎培尔在下面这段话中预示了还是个孩子的麦克斯韦未来的工作:
但是他最感兴趣的事还是户外活动…跨越沟渠,爬树,看着树倒下,并且在它们倒下时爬上去进行盛大的游戏,在七月的热天去捅马蜂窝,吹肥皂泡,惊异于它们颜色的改变…
我相信对一个年轻男孩子来说,从正在倒地的树上往下跳,捅马蜂窝来玩是非常刺激的,但是他对肥皂泡的兴趣才说明了他的未来。
在亚里斯多德时代之前,光的本质便成为人们思考的课题。在麦克斯韦之前的一个世纪里,牛顿理论和惠更斯理论(图3)在为征服自然哲学家的思想而进行着竞争,在那时,他们被认为是物理学家。牛顿认为,光是很小的微粒,颜色是由于微粒加速穿越以太时发生振动而产生的。惠更斯认为光完全是一种波动现象,是在以太中进行传播的。

图 3 (a)牛顿和(b)惠更斯在18 世纪提出了具有竞争性的光理论(微粒与波)。
托马斯·杨证明肥皂泡上的颜色是波相互干涉的结果,从而支持了惠更斯的波理论。然而,这个假设还有一些困难,这是麦克斯韦在15 岁时便看到的。坎培尔这样记录着:
在 1847 年的春天…他的叔叔,约翰·柯(JohnCay) 先生,…带着詹姆斯和我…去看望尼可( Nicol ) , 戴 维 · 布鲁斯特( David Brewster)先生的朋友,他是偏振棱镜的发明人。即使在此之前,詹姆斯通过冰洲石已经被“偏振光”吸引了,…但是这次访问又为他对这种现象的兴趣增添了新的重要的动力,以及由此而产生的思考。
冰洲石是一种纯净的晶体形式的方解石,是双折射性的。在一个极化方向有一个折射率,在与之相正交的另一个极化方向上有另一个折射率。如果在纸上画一条线,将水晶放在纸上,你可以看见两条线。二个未经极化的光束射到晶体上,这个光会被分成“常规光束”和“非常规光束”。尼可找到一种方法可以将两块冰洲石相粘合来将两种光线分开。
尼可对年轻的麦克斯韦印象极其深刻,他给了麦克斯韦两套偏振棱镜。回到家后,麦克斯韦把玻璃迅速熔化,然后将其倒入模具中。他随后将玻璃迅速冷却,这样在玻璃中便存在着很大的应力。他将一块偏振棱镜放在玻璃的后面(“偏振仪”),第二块棱镜放在玻璃的前面(“分析仪”)。他制作了一个显画器,并且亲手做出了玻璃应力模式的水彩画,见图4。然后,他解出了斯托克斯(Stoke's)方程,并且将测量和计算结果发表在文章中。

图4 作为一个少年,麦克斯韦使用偏振光探索了在未经过退火的玻璃中的应力。因为光被极化了,因此它必须是横波,这是光的波理论所面临的主要困难。
有两个原因使得这件事情变得意义重大。首先,麦克斯韦实际上在进行场的工作。应力和张力纯粹属于力学,完全属于物理场;没有什么抽象的意义,但他们都是场;(一个场是在空间内定义的一个矢量)。
第二个具有明显意义的是这个实验所展示的与光的波理论相关的关键问题。声音是一个纵波。空气在发射机到接收机这条线上来回振动。因此,它无法被极化。另一方面,不存在在媒介中(空气)传播所存在的剪切强度的问题。
如果波被极化了,它必须从一边-向-另一边进行横向振动。它能够上下振动(垂直极化)或一边-向-另一边振动(水平极化)。一个小提琴的弦(图2)产生一个横向驻波。一个波必须有一个让它可以在其内进行振动的媒介(记住,这是在19 世纪),这几种未被探测到的媒介被称为以太。以太的剪切强度必须为零。例如,星光在这个以太中通过振动向我们走来。而地球在它的轨道上没有阻力地穿过同样的空间。
问题是,你如何可以在一个没有剪切强度的媒介中得到一个横向起伏的波?光的波理论毕竟还不是完美无缺的。
麦克·法拉第(Michael Faraday)(图5)随后进入了人们的视野中。就在麦克斯韦出生后几个月,法拉第正在进行着磁感应实验。这似乎是在做非常合理的事。给出一个线圈,电便会产生磁。因此,根据对称性的本质,为什么磁不能产生电呢?以前曾多次试图进行实验,但全都失败了。磁不能产生电,法拉第经历了相同的失败。
等等!那是什么?法拉第注意到当他打开实验用的开关时,他的仪表出现了轻微的晃动。合上开关。又一个轻微的晃动。他得到了。窍门是须将磁铁接通和关闭时才能得到它。磁的感应需要一个变化的电流。随后出现了发电机。注意我还没有提到磁场;这个概念在那个时候还不存在。
法拉第来自于一个贫穷的,地位卑下的家庭,没有受过大学教育,并且也没有什么数学技能。然而,他具有超凡的直觉。他观察到了沿着磁铁“力量线”的磁以太的涨落而产生的感应(与光以太不同)。他将磁以太的状态称为“电紧张状态”。存在两个问题:法拉第没有数学技能来发展他的思想,并且“远距离的作用” 概念在那个时候已经牢固地树立起来并且得到了确认。
由普利斯特里(Priestly)首先提出,随后是卡文迪什(Cavendish),库伦(Coulomb)使用扭力平衡将远程作用进行了量化。按照这个理论,两个电荷之间的作用力与它们之间距离的平方成反比。对于磁力也同样适用。确实,当事情发生变化或移动时,便出现了困难,但已经做了一些尝试来解释说明,那么为什么要抛弃别人已经做了的工作,而要使用法拉第复杂的,想象出的力量线呢?
更重要的是,由于在重力作用物体之间缺乏力学连接,从而使得牛顿对此不是很满意,但牛顿还是用它的万有引力理论解释了远距离作用力的正确性。将这些现象纳入牛顿理论框架中是很重要的,因为,那时牛顿是物理界的上帝。如果你在物理方面的工作不能推回到f =ma 及牛顿,你不用奢望别人会认真地对待你。
当麦克斯韦20 多岁,还是剑桥大学的学生时,他便开始进行法拉第的力量线的工作。当他得到了Aberdeen 的教授职位而离开剑桥时,他的工作便中断了,在这期间,麦克斯韦进行了土星环的构成方面的研究[4][见图3(b)]。通过他发表的文章,麦克斯韦树立了其具有一流数学能力的声望。
麦克斯韦在随后的几年时间里进行了法拉第力量线的工作(这只是他所做的许多事情中的一件,包括色彩的感知和热力学),他在1865 年发表的动态电磁理论中对其研究工作的积累做了总结。这个震撼世界理论的发表,恐怕是整个世纪中最重要的事件,它受到了许多赞美…一个伟大的呐喊!后来发生了更多的事。
要知道麦克斯韦的理论是如何开发的,我们研究一下他所发表的描述工作进展的三篇文章。第一篇是“关于法拉第力量线”[5],发表于1865 年,当时他是24 岁,就在他离开剑桥去Aberdeen 之前:
此时还不能使用任何电理论,除非它不仅可以反映静态的电与电流之间的关系,同样可以显示出两种状态的电的吸引和感应效应。这种理论必须能准确地满足这些定理, 即所知晓的数学形式,还必须提供一种方法来计算当这些公式不再适用时的极限情况。因此,为了满足这些科学要求,学生必须使自己熟悉大部分最错综复杂的数学,仅仅将它们记在脑中而不去应用是会阻碍自身的进一步发展的。

图 5 麦克·法拉第(Michael Farady )发现了磁感应,并且提出了力量线,从而产生了麦克斯韦的电磁理论。
在这里我们看出那个时期的物理已认识到电流仅仅是运动的静态电。他们还不知道这种电流的形式,甚至不知道它是否有两种形式的流动(正方向和负方向),当其中一种流动形式不存在时,便是第二种流动形式,或者是两种形式的混合。
我们同样看到麦克斯韦的目标是将静态的电效应与电流效应相联系。他意识到很难将所有存在的极其复杂的部分结果协调进入一个统一的理论中。
他进一步强调“这种简化的结果可以用纯数学公式表达或一个物理假设的形式来表达”。
麦克斯韦在这里指出数学抽象的这种折衷会忽略事实。但是通过物理模型,你可能只能得到一个部分的解释。他指出自己的研究是数学的,但会紧密地与物理模型相联系,从而可以吸收两种方式的优点。麦克斯韦随后完全摒弃了物理假设,但在那个时候,物理模型是很重要的。如果麦克斯韦想要受到别人的认真对待,则必须在某些地方出现牛顿和f = ma。
麦克斯韦经常引用他的好友威廉姆· 托马斯(William Thomson,后来叫做Lord Kelvin)的工作,指出自然界中常见的相似性。
我们已经发现热在均匀媒介中的均匀移动与那些与距离的平方成反比的吸引力的变化是相同的。我们只需用中心引力来替代热量,任何一点的吸引力的加速度来代替热流,用势能来代替温度…
麦克斯韦在这篇文章中使用“比拟思维”,用液体流动来解释电磁力。麦克斯韦定义法拉第的力量线是一个无惯性物体在磁力作用下的运动路径。麦克斯韦随后想象出在每一个法拉第力量线上有一个管子。这个管子是有尺寸的,因此一个单位的流体总是在单位时间内在这个管子中流过单位长度。这意味着在距离磁铁的某些距离上,由于流动速度(磁力)变小,而使得管子变大。麦克斯韦指出管子在任何地方都不存在未占用空间;磁力像不可压缩的液体一样流动着。
麦克斯韦指出知道了在闭合表面流动的液体,根据已知的传导定律便可决定(无源的)其在内部的整个体积内的流动。磁力是由这个流体的压力之差所决定的,磁导率(现代用的名词)可以解释为流体流过管子的容易程度。类似的模型可被用于静电问题。
麦克斯韦急切地告诫读者:
通过将假想的流体运动中的一切都用纯几何来表示,我希望能够获得其一般性和准确性,避免从自称可以解释造成这种现象之原因的不成熟的理论所带来的危险。
麦克斯韦强调,他并不想假设某种流体的流动实际上引起了所观察到的电磁力。相反,他试着用与流体流动的类似性来看看是否对将来的研究有用。麦克斯韦文章中剩下的部分逐渐地开发了一个流体流动的详细的数学理论,并且显示出它如何对电磁力产生类似的结果。
想像中的或其它方式的不可压缩的流体流动是不可能支持像光这样的横波的。1862 年,在麦克斯韦30 岁时发表的第二篇文章[6],“关于物理力量线”中,麦克斯韦保留了物理模型的模拟性:
我现在建议从力学的角度来研究磁现象,并且确定什么样的媒介中的张力或媒介中的运动能够产生所观察到的力学现象。如果在同样的假设条件下,我们能够将电磁现象中的磁性吸引现象与所感应电流的现象联系起来的话,我们就已经找到了一种理论,如果不对的话,只能由实验来证明是错误的。这个实验可以极大地扩展我们对这部分物理的认识。
历史学家们承认麦克斯韦是 19 世纪最伟大的物理学家,与爱因斯坦和牛顿齐名。
这个新的力学模型仍然采用了流体,但现在流体中充满了涡流。这些涡流围绕着法拉第的力量线。这些力量线是流体的张力,张力是由涡流产生的。麦克斯韦所提供的一个例子(见图6)显示出磁铁的北极(图6(a))是镶嵌在均匀“磁力场”之中的(磁场的概念那时仍然不存在)。磁铁的南极是镶嵌在同一个磁场之中的(图6(b))。当力量线(来自磁铁和来自均匀场)是同向时,涡流相加(产生张力,从而产生磁力)而增大。当力量线反向时,结果相反。净效应是磁铁会受到一个力矩试图指向北极,就像指南针一样。
麦克斯韦给出了对这个力学模型详细的数学分析,指出涡流周边的周转率与磁力成正比,并且流体的密度与“产生磁感应的介质的容量”成正比,即,磁导率。
麦克斯韦并不知道这些涡流究竟是什么,但是他认为这可能是电流以某种方式产生的。
图 6(b)特别重要:
我们应当总是用箭头来标出方向,我们必须沿着这个箭头方向才能看到涡流是沿着手表指针的方向来旋转的。这个箭头便指出了磁场中朝北的方向…
这是我所看到的最早发表的右手定则的描述和示意,最近也同样被用作IEEE 的标志。

图 6 (a)1862 年:当力量线是同向时,麦克斯韦演示出它们的力量线是相加的,将罗盘的北极指针拉着指向北。(b)麦克斯韦使用的右手定则。
在麦克斯韦之前的一个世纪,牛顿理论和惠更斯理论在为征服自然哲学家的思想而进行着竞争,虽然他们那时都被认为是物理学家。
麦克斯韦指出涡流模型没有解释电流,这个模型还有一个很明显的问题:
我已经发现很难将媒介中存在的涡流在同样方向上以并行形式一排一排地旋转表达出来。相邻涡流的联接部分必须以相反方向来运动;很难理解媒介一部份的运动如何能够和与之相连的另一部份进行相反运动的媒介共存。
为了修正这个问题,麦克斯韦插入了“一个粒子层作为一个空载层来介入”,如图7 所示。这个粒子层允许涡流按相同方向进行旋转。他同样用这些粒子来模拟电流作为粒子的净运动。麦克斯韦指出,与涡流相比,这些粒子的尺寸和质量非常小。他还指出,它们的转动在分子内部没有产生滑动和碰撞。但是如果它们从一个分子传到另一个分子,它们便会受到阻力,并且产生热量。在今天看来,这些模型或多或少与导体中的“电子海”相类似,涡流是导体的原子,空载轮是电子。
这个力学系统同样可以模拟静电,麦克斯韦对今天被我们称之为极化的电荷进行了描述:
在被感应的电介质[静电]中,我们可以想象每个分子中的电被移动了,一端显示出正的极性,一端显示出负的极性,但电是完全与分子整体连接在一起的,因此没有从一个分子穿越到另一个分子内。
麦克斯韦随后指出这种电的位移并不是电流,因为它还是被束缚在涡流之中的,但“它是电流的开始”。涡流被赋予了一定程度的弹性,这样,当位移中止时,移动的电荷又弹回到分子中。这看来似乎是麦克斯韦位移电流的开始,他将这个关键项加入到今天被称为麦克斯韦的方程中。
既然涡流有弹性,力学模型便可以支持横波,从测量的电气和磁力弹性所计算出的横波速度与测得的光速吻和得很好。因此,麦克斯韦提出光和电磁波现象可能是同样媒介的波动引起的。他还没有真正提出实际上光本身可能就是电磁。
麦克斯韦的主要文章[7],题为“电磁场的动态理论”,是在1864 年底才被宣读的(在一次会议上介绍的),当时麦克斯韦是33 岁。在这篇文章中,他完整地提出了电磁理论,但它还不是我们所熟悉的4 个方程。首先,麦克斯韦没有使用现代矢量代数,这是在麦克斯韦去世后由吉布斯(因Gibbs 现象而著名)所推导出的(见图8)。在这篇文章中,麦克斯韦用迪卡尔坐标系中的三个标量方程来表示矢量差分方程。后来,在他论文的第三版中[8],他使用了“四元法”,将事情变得更糟了[9]。在这篇文章中,麦克斯韦确实使用了,但他仅仅是为了标记上的方便。
其次,麦克斯韦以磁矢量势能(这便是法拉第的“电紧张状态”(electrotonic state))为主。磁场和电场为次。亥维塞(Heaviside)注释到[9]:“我一直没有任何进展直到我将所有的势能都扔掉,而将E 和H 作为注意的对象…”
坦率地说,亥维塞同样注意到了现代的全双工形式(这种形式显示出了E 和H 的对称性,是由亥维塞推导出的):
…带来了许多有用的联系,这种联系以前是由于被隐藏在矢量势能的干涉和其杂散的表示而未能看到。
麦克斯韦在这篇文章中提出了含有20 个变量的20个方程。亥维塞用数学手段将它们放入现代的形式。赫兹(Herz)(见图9)通过对在距离模型中的作用施加一个无限系列的局部修正也独立地推导出了同样的现代形式的方程。两个人都废弃了用作主要参数的势能。具有讽刺意义的是,物理学家们现在又回过头来将势能作为主要参数[10]。
麦克斯韦在这篇文章中指出:
我所提出的理论可能被称为电磁场,因为它是与电或磁铁自身的周围空间有关的…
他还指出:
电磁场是在电或磁的条件下含有实体及围绕在实体的空间部分。
对于我来说,这意味着麦克斯韦是使用术语“场”来代表一个感兴趣的区域,就好比“战场”。我这么强调是因为这是一个个人观点;历史学家们很可能具有不同的观点。我不知道矢量场的概念是什么时候正式引入的。然而,正如上面所提到的,我们确实知道正式的矢量代数是在麦克斯韦去世后才引入的。
我个人的印象是麦克斯韦完全意识到了他所引入的位移电流的重要性,因为,他将它放在自己理论的第一组的三个方程中。然而,由于麦克斯韦谦虚的个性,他没有提及它的重要性。在现代版本中,这一套迪卡尔坐标的三个标量方程说明总电流是传导电流和位移电流之和,在这里用其在文章中的表示方法完全相同的形式表示出来:
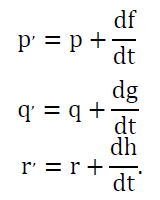
历史学家着重强调的是麦克斯韦没有将位移电流加进来达到其方程的对称性。在麦克斯韦所表达的20 个等式的方程中,对称性是很明显的。事实上,麦克斯韦没有将对称的磁荷或电荷包含进来;是亥维塞将它们加入进来的。历史学家们还指出并不完全清楚是什么灵感促使他将位移电流加入的,但在我看来,这似乎与上面所描述的边界电荷的类似性有关。麦克斯韦确实在“所谓的真空”中提到了传播问题,并且指出EM 力不是由物质传播的,但必须是由某种即使在真空中也存在的以太类的物质来传播的。
当麦克斯韦 20 多岁,并且还是剑桥大学的学生时,便开始进行法拉第的力量线的工作。
就是在这篇文章中,在测量和计算结果相等的基础上,麦克斯韦最后得出结论:
这个速度与光的速度是如此接近,以至于我们有强有力的理由来得出结论,光本身(包括辐射热,和其它辐射,如果存在的话)是按照电磁定律以波的形式传播通过电磁场时所产生的一种电磁扰动。
当测量磁导率和介电常数时,麦克斯韦确实开玩笑地进一步指出,“在实验室中光的唯一用途是能看见仪器”。
这篇文章中最显著的是麦克斯韦完全放弃了力学模型。虽然仍然存在力学模拟对比,并且他的理论中是以出现EM 力为结果的,但缺少力学模型则意味着,牛顿,整个物理界的上帝,与这个理论内在的工作原理是毫无关系的。从政治上说,这是个坏消息;但麦克斯韦从来就不是个搞政治的。
让事情变得更糟的是,麦克斯韦特别谦虚。例如,在1870 年,他担任英国科学促进协会A 部的主席。他的就职演说发表在新的自然杂志的第二卷。麦克斯韦演讲的大部分用来宣传他的好朋友开尔文勋爵(LordKelvin)的多少有些荒诞(用今天的标准来看)的原子理论,而不是宣传他自己的EM 理论。在结束时,他提到,“我要介绍的另外一种电的理论…”甚至没有用自己的信誉来推荐自己的理论。
弗雷曼·代森(Freeman Dyson)在一篇论文[11]中指出了这一点,在这篇文章中他讲述了物理学家迈克尔·扑平(Michael Pupin)的例子。扑平在1883 年从美国赴剑桥向麦克斯韦本人学习麦克斯韦理论时,才发现麦克斯韦已于四年前去世了。然后他发现整个剑桥大学竟然没有一个人可以讲授麦克斯韦理论。他最后到德国,向亥姆霍兹(Helmholtz)学习麦克斯韦的EM 理论。扑平回到美国,在那儿他在哥伦比亚大学向一代又一代的学生讲授EM 理论。
麦克斯韦随后指出这种位移电并不是电流,因为它被束缚在涡流中,但它是“电流的开始”。
今天我们经常会认为电场和磁场是实际存在的。其实并非如此。这些场纯粹是抽象的数学结构,可以让我们预测实际上会观察到的现象。
正如代森指出的,我们可以很容易地理解和测量诸如能量和距离这样的事物。我们可以用焦耳每立方米来表示与E2 成正比的电能密度。用热量计来测量焦耳。用一根棍子来测量距离。但是我们如何来直接测量电场?你首先需要一个热量计的平方根。然后,用什么样的棍子来测量立方米的平方根?我们只能通过直接测量的如焦耳,牛顿和米来推断麦克斯韦的抽象的电场。
如果我们不能直接测量或感受电场或磁场,那么它们有什么好处呢?正如代森所指出的,当我们解出了这些场后,便可以产生实际上可以感受和测量的量,如E2,H2 或E×H。我们在量子电动力学中也有同样的情况(QED,麦克斯韦理论只是它的一个特殊例子),正如理查德·费曼极为干练的描述[12](见图8)。
麦克斯韦理论经过了20 年才被认识到它究竟是什么。这至少部分地由于它的复杂性(当在一个距离上的作用力工作得很好时,为什么还要操心这些复杂的“场”的问题呢?)。这同样还归因于缺乏基本的力学模型(由于这个原因,直到开尔文勋爵进入坟墓,他还坚信麦克斯韦的理论是不正确的)。最后,还由于麦克斯韦自己的谦虚。
同样在这篇论文中,代森提出由于麦克斯韦的谦虚使得物理界受了20 年的挫折。这个失败并不是由于没有意识到麦克斯韦方程本身的重要性而使物理界受了20年的挫折;相反,是由于没有认识到麦克斯韦用抽象的数学所打开的与牛顿毫无关系,并且没有任何借口通过事实来理解现实的新世界。根据代森所言:
麦克斯韦理论的最根本的重要性远远超出他的最直接的成就,即能够解释并且将电学和磁学统一起来。它最根本的重要性在于成为二十世纪所有重大成功的框架。它是爱因斯坦相对论的模板,是量子力学的模板,…以及熟知的将场和粒子统一起来的理论,粒子物理的标准模型。所有这些理论都是基于麦克斯韦在1865 年所引入的动态场这个概念之上的。
所以这便是麦克斯韦的遗产,它用通过数学抽象出来的场的概念将物理从牛顿力学的禁锢中解脱出来,为20 世纪物理学的重大进步做好了准备。
作者: James C.Rautio IEEE microwave magazine
参考文献
[1] New DMLs for 2005–2007 named [Online]. Available: http://www.mtt.org
[2] L. Campbell and W. Garnett, The Life of James Clerk Maxwell, 2nd ed. London:Macmillan, 1884.
[3] J.C. Maxwell Biography [Online]. Available: http://www.sonnetsoftware.com/bio/maxwell.asp
[4] S.G. Brush, C.W.F. Everitt, and E. Garber, Maxwell on Saturn’s Rings. Cambridge,MA: MIT Press, 1983.
[5] J.C. Maxwell, “On Faraday’s lines of force,” Trans. Cambridge Philosoph. Soc.,vol. X, Part I. 1855. Repr. The Scientific Papers of James Maxwell, 1890. New York:Dover, pp. 155–229.
[6] J.C. Maxwell, “On physical lines of force,” Philosoph. Mag., vol. XXI, Jan–Feb.1862. Repr. in The Scientific Papers of James Maxwell, 1890. New York: Dover, pp.451–513.
[7] J.C. Maxwell, “A dynamical theory of the electromagnetic field,” in Royal Soc.Trans., vol. CLV, Dec. 8, 1864. Repr. in The Scientific Papers of James Maxwell,1890. New York: Dover, pp. 451–513.
[8] J.C. Maxwell, A Treatise on Electricity and Magnetism, 3rd ed. New York: Dover,1954.
[9] P.J. Nahin, Oliver Heaviside: Sage in Solitude. New York: IEEE Press, 1987. Repr. with a new introduction. Baltimore, MD: Johns Hopkins Univ. Press, 2002.
[10] F. Gronwald and J. Nitsch, “The structure of the electromagnetic field as derived from first principles,” IEEE Antennas Propagat. Mag., vol. 43, pp. 64–79, Aug.2001.
[11] F. Dyson, “Why is Maxwell’s theory so hard to understand?” in James Clerk Maxwell Commemorative Booklet, Fourth Int. Congress Industrial and Applied Mathematics, Edinburgh, Scotland, July 1999.
[12] R.P. Feynman, QED: The Strange Theory of Light and Matter. Princeton, NJ: Princeton Univ. Press, 1985.

 粤公网安备 44030902003195号
粤公网安备 44030902003195号