计算电磁学基础知识及数值方法汇总

积分方程类方法主要包括各类基于边界积分方程(Boundary Integral Equation)与体积分方程(Volume Integral Equation)的方法。与微分类方法不同，其未知元通常定义在源区，比如对于完全导电体(金属)未知元仅存在于表面，显然比微分方程类方法少很多;而格林函数(Green’s Function)的引入，使得电磁场在无限远处的辐射条件己解析地包含在方程之中。场的传播过程可由格林函数精确地描述，因而不存在色散误差的积累效应。

(3)计算电磁学常用方法汇总

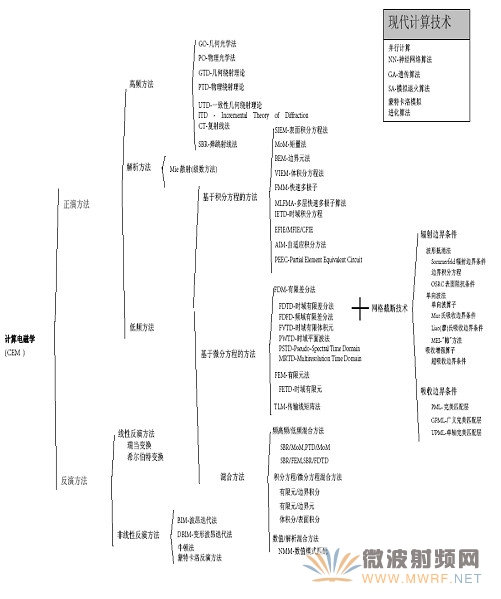
(4) 几种主要方法之间的比较

这里对计算电磁学中几种主要的数值方法进行简单的比较，即时域有限差分法(FDTD)、有限元(FEM)、矩量法(MoM)、多极子法(MMP)、几何光学绕射法(GTD)、物理光学绕射法(PTD)和传输线法(TLM)。

性能	MoM	GTD/PTD	MMP	FDTD	FEM	TLM
使用求解的问题	天线建模、线建模和表面结构、导线结构的问题	大电尺寸结构的范围的应用	直接计算，不需要中间步骤	可以直接求解麦克斯韦方程	电的和物体几何尺寸的特性可分开定义和处理	所有的场分量可以在同一点进行计算
数值建模特点	可以对任意结构形状的物体上的电流结构建模	在高频散射问题中非常有效，例如雷达散射截面问题		不需要存储空间形状参数	可以克服FDTD中必需的阶梯建模空间问题	可用于非均匀煤质建模和分析
适于计算电磁场的区域	辐射条件允许求解在辐射物体外的任何地点的E和H场	满足远区平面波近似的空间，节省计算机资源		很容易对非均匀煤质的场问题建模	适于分析复杂结构，对内部EM问题建模有效	适于分析复杂结构，对表面域建模很有效
适于研究的问题	计算天线参数、输入阻抗、增益、雷达问题			对内部复杂煤质问题可以有效地建模	可以对非均匀煤质问题建模	比FDTD有较小的数值色散误差
数值建模中存在的问题	对内部区域建模问题困难大	几乎不提供有关天线参数的信息	场强以外的其它参数必须进行计算	对无边界问题需要吸收边界条件处理	对无边界问题需要对边界进行建模	比FDTD使用更多的计算资源
计算机实现遇到的问题	在非均匀煤质中会遇到困难，要用大量的内部资源，所以，通常只用于低频问题	只在高频有效，不能提供任何电流分布的情况	计算密集型，占用的计算量和内存都很大，使用者必须熟悉多极子理论	计算密集型，有数值色散误差，内存量大	计算密集型，处理开放区域内的封闭面上的未知场点问题难	带宽受色散误差限制，不能解围绕散射体和需要大空间的问题
计算场强以外的其它物理量的能力		只能计算远区场		计算场传播和电流分布等参数很难		同FDTD