共形微带天线的全波分析

摘要：本文以柱面、球面等规则形状微带天线为例，采用基于面积分方程法研究了共形微带天线的特性。采用细条带等效探针馈电模型，通过引入半Rao-Wilton-Glisson (RWG) 函数以及边界电荷，分析了电压源以及电流源模型中阻抗矩阵Z 以及V 向量的计算过程。针对共形微带天线阵列未知量大、效率低的缺陷，采用特征基函数法结合等效偶极矩法分析了共形微带天线阵列。数值计算证明了本文分析的正确性和有效性。

1、引言

在飞机、导弹等高速飞行的载体上，要求天线不能影响载体的动力学特性，除了将天线安装在天线罩中外，还可以使天线与载体物理共形，近年来可穿带技术也需要共形天线技术。微带天线具有易共形的特征，因此共形微带天线研究成为热点。目前，研究较多的为柱面[1]、球面[2]等规则形状微带天线，研究方法从简单的、精确度较差的传输线理论、腔模理论过度到复杂的、精确度高的全波分析理论。这里，我们采用全波分析理论，实现对共形微带天线的精确分析。

积分方程法是全波分析理论中的一种常用方法，在分析共形微带天线时，主要采用两类积分方程法，应用较多的是体面积分方程法[3]，这种方法适用范围广，理论上可以分析电小尺寸、任意曲面的共形微带天线，且计算过程简单。该方法对天线进行整体剖分，导体面和介质体一般采用三角面剖分和四面体剖分，采用矩量法求解表面等效电流和体等效电流。但其计算大尺寸阵列时会产生庞大的未知量，甚至容易产生内存溢出的现象。虽然，借助于快速算法可以扩大体面积分方程法的应用范围，但其消耗的计算机内存也是相当大的。在载体面规则的情况下可以采用另一类方法-基于分层媒质格林函数的面积分方程法[4]，这种方法只需将导体面进行剖分，介质体不需要进行体剖分，其影响体现在该结构下的并矢格林函数里。这样，产生的未知量相比体面积分方程少的多，缓解了计算机内存压力，适用于较大尺寸的阵列分析。本文采用的即为第二类积分方程法。

采用面积分方程法分析的重要环节是对相应载体结构的并矢格林函数的求解，以柱面、球面为例，本文采用面积分方程法分析了共形微带天线的性质。天线模型采用细条带等效探针激励的方式，通过引入半RWG 函数以及边界电荷，成功构建了一种可行的激励模型，重点分析了矩量法过程中阻抗矩阵以及电压向量的计算。另外，本文利用快速算法分析了共形微带天线阵列的辐射特性，为共形微带天线的研究提供了理论支撑。

2、理论分析

共形微带天线结构如图1 所示，分层结构第一层为空气层，第二层为介质层，最内层为金属接地导体。图中任意形状的贴片为不计厚度位于介质层与空气层的交界面上。

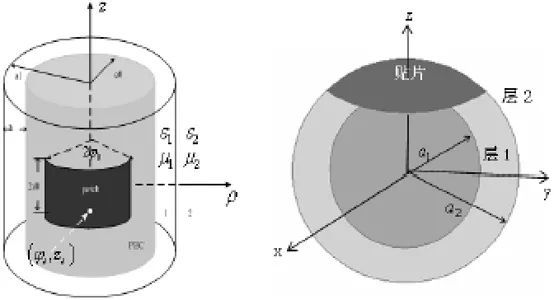
​图1、共形微带天线示意图

正如引言所述，本文采用面积分方程法对其进行分析，根据贴片与探针表面切向场为零，采用伽略金法的矩量法求解，其阻抗矩阵可以表达为

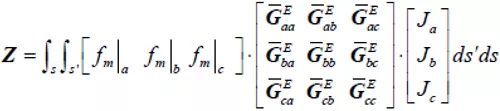
​(1)

其中，fm为检验基函数，下标a,b,c 为相应坐标系的三个分量，分析柱面采用柱坐标系下的ρ, φ, z，分析球面采用球坐标系下的θ,φ, r。

G为并矢格林函数。J 为贴片和探针表面的电流，需要对贴片和探针进行三角形离散，采用RWG 基函数模拟表面电流。在此过程中，并矢格林函数的求解是首先要解决的难点之一，目前，关于柱面，球面情况下并矢格林函数的求解已有不少成果[5-7]，本课题组对两种情况下求解格林函数做了大量工作[8-11]，这里归纳出两类格林函数之间的异同，它们在以下两个方面相似：

(1) 除了细节差异，两者主体推导思路相似，都是基于复杂媒质中波的传播理论为基础。

(2) 两者场型格林函数都表现出了收敛速度慢的缺陷，都可以采用相似的方法-格林函数渐近项提取的方法来改善格林函数的收敛速度。

在以下两个方面有所不同：

(1) 在函数形式上不同，柱面格林函数为积分形式，而球面格林函数为双级数和形式。

(2) 在推导过程中，柱面结构中TE 波与TM 波发生耦合，而球面结构中TE 波与TM 波不发生耦合。

鉴于篇幅限制，不再对两者详细的推导过程做出解释。根据矩量法，求解出天线表面的等效电流，即可得到天线特性。

3、激励源的构建

在分析过称中需要考虑的是激励源的构建，本文中采用RWG 函数来模拟贴片与探针的电流分布，激励源并不能采用常用的边馈法，RWG 函数边馈法要求在两个三角形的公共边上添加δ源。此处由于探针底部的边并不是三角形对的公共边，而是边界边，RWG 函数在边界边上并没有定义，如图2 所示。

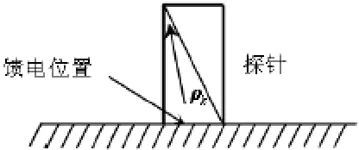
​图2、探针底部示意图以及半RWG 函数

这里，引入了半RWG 函数，顾名思义，半RWG 函数只在一个三角形上定义，其形式为[12]

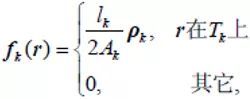
​(2)

其中，Ak表示三角形Tk的面积；lk表示边界边的长度；ρk代表Tk边界边对应角点到三角形内任意点的矢量。该三角形上的电荷密度为

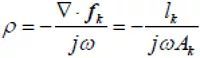
​(3)

则Tk三角形内的电荷为-lk/ jω，根据电荷守恒定律，边界边上的电荷为lk/ jω，电荷密度为

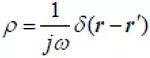
​(4)

δ(r-r’)表明电荷只分布在边界边上。需要说明的是，这里只在激励源处定义了半RWG 函数，其他边界边不需要定义。此时，可以添加电流源，也可以添加δ电压源，具体分析过程可参考文献[12]。在矩量法分析中，需要求解阻抗矩阵Z 和电压矩阵V。

电流源激励是将稳定的电流源添加在探针底端的一个三角形上，可以采用半RWG 函数的形式，电流密度系数为1，为

​(5)

根据矩量法，V 矩阵可表示为

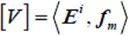
​(6)

电压源激励时的V 矩阵比较简单，在探针底端馈电边为lnV ，其他公共边上为零，即

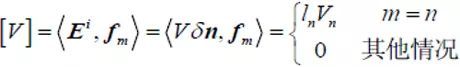
​(7)

在分析过程中，我们得到如下结论[12]：当天线剖分网格相同时，电流源激励比电压源激励少一个激励源处的基函数，得到的电流分布并不相等。电流源激励的阻抗矩阵为电压源阻抗矩阵的一部分，少了激励源处自阻抗元素以及互阻抗元素。电流源处的自阻抗元素和互阻抗元素用于求解V 矩阵以及输入阻抗。虽然电流源与电压源激励分析角度有所区别，但最终得到吻合一致的输入阻抗值。

4、共形微带天线阵列的计算

分析共形微带天线阵列会面临未知量多、计算效率低的缺陷，需要结合快速算法来改善效率。特征基函数法是适合分析本文对象的一种算法。目前，特征基函数法结合其他算法被广泛应用于对电大尺寸目标的散射与辐射分析[13]。它通过将目标分成若干子域，降低阻抗矩阵的维数，对各个分块操作提取主特征基函数与次特征基函数，进而构造一个降阶的阻抗矩阵。

首先，将阵列天线进行分块，由于阵列天线是贴片个体组成的，可以将单个贴片视为一个子域，这样不需要考虑子域连接处电流的不连续性。

其次，为了反映子域间的耦合作用，要对每个子域提取次特征基函数，第一阶次特征基函数通过其他所有子域主特征基函数产生的场计算出来的，同理，第二阶次特征基函数通过其他子域第一阶次特征基函数产生的场得到的，以此类推，可计算出任意高阶的次特征基函数。

在分析过程中，有几点需要注意：

(1) 由于贴片都是相同的，因此可以将贴片剖成相同的数据网格，这样所有子域的主特征基函数相同，降低了计算的复杂度。

(2) 在得到次特征基函数时，需要计算子域间的互阻抗矩阵，对于周期性天线阵，我们可以根据子域间的相互位置关系以及矩阵本身的对称性来减少互阻抗矩阵的计算。

(3) 通过设置门限进一步减少互阻抗矩阵的计算，门限的设置忽略了远距离或者耦合弱的子域产生的次特征基函数，多次试验经验表明，当两个子域间的距离超过2λ时，其产生的耦合作用即可忽略。

(4) 对于非周期性天线阵列，子域间的相对位置关系并不固定，因此考虑子域间的互阻抗矩阵个数会跟多，这里可以采用等效偶极矩法进行近似计算，可以提高计算效率。限于篇幅，不再介绍等效偶极矩的原理。

5、天线数值计算

本文计算了一副条带馈电圆柱共形微带天线的输入阻抗和辐射特性。圆柱结构如图1 所示，接地圆柱半径a0=50mm，介质厚度h=0.795mm，介电常数ε1=2.3 ， 贴片高度2d0=30mm， 宽度2a1φ0=40mm ，φs=0°，zs= 10mm。激励源采用电源激励。仿真计算输入阻抗结果如图3 所示，与文献[14]吻合较好，说明了本文处理的正确性。

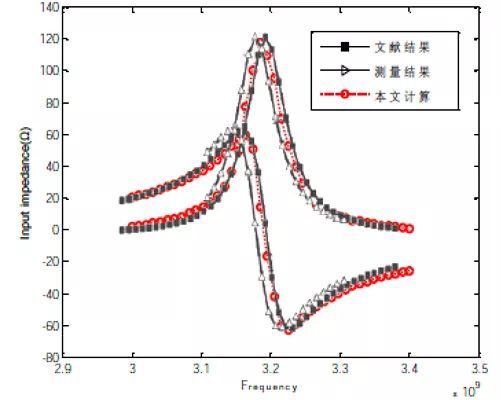
​图3、柱面共形微带天线的输入阻抗对比图

另外，本文计算了一副球面非周期对称阵列微带天线，排列方式按照图4 的二十面体网格形式排列，矩形贴片的尺寸为7.2X5 mm2，金属球体半径为76 mm，介质厚度为0.25 mm，介电常数为2.94，探针距离贴片中心的弧长度为1 mm。围绕中心阵元的第一圈的弧长度为15 mm，第二圈的弧长度为30 mm，每一圈内的阵元之间的弧长度都相等，激励源采用等幅同相的电压源。工作频率为16.2 GHz。

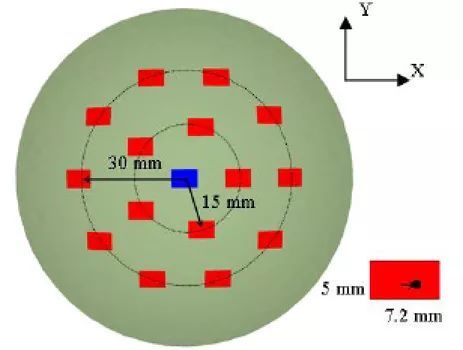
​图4、非周期排列的阵列模型俯视图

这里采用FEKO 仿真结果加以对比，如图5所示。需要指出的是FEKO 软件采取天线整体全剖分方式，未知量数目多，接近计算机内存最大值，而本文内存消耗几十兆，节省了内存。从图中可以看出，本文分析计算的正确性。

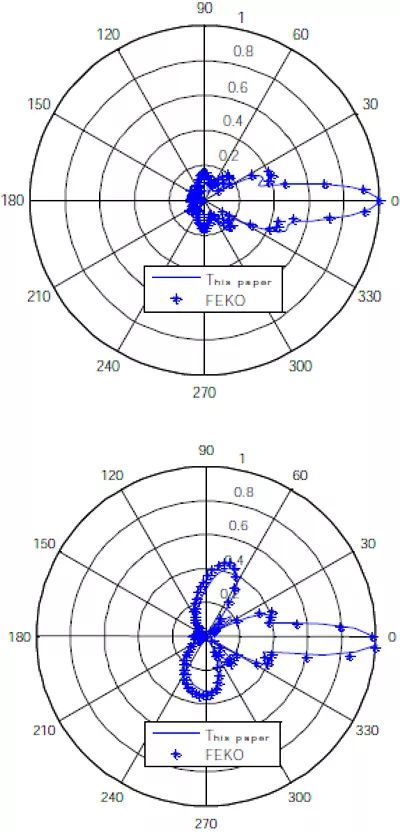
​图5、非周期排列的阵列E 面与H 面远区场图

6、结论

本文以两种曲面为例，采用了面积分方程法分析了共形微带天线的性质。天线模型采用细条带等效探针激励的方式，通过引入半RWG 函数以及边界电荷，成功构建了一种可行的激励模型，分析了矩量法过程中阻抗矩阵以及电压矩阵的计算。另外，本文利用快速算法分析了共形微带天线阵列的辐射特性。

参考文献

[1] Wu J, Khamas S K, Cook G G. Moment method analysis of a conformal curl antenna printed within layered dielectric cylindrical media[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(7): 3912-3917.

[2] T. Yu and C. Y. Yin, ―Analysis of L-probe fed-patch microstrip antennas in a multilayered spherical media,‖IEEE Int. Sym. Antennas Propag., Nanjing, China, 2013: 376-379.

[3] Zhang K, He M, Xu X W, et al. An efficient solution of the volume-surface integral equation for electromagnetic scattering and radiation of the composite dielectric-conductor objects with reduced number of unknowns[J]. IEEE Transac- tions on Antennas and Propagation, 2013, 61(2): 798- 808.

[4] Khamas S K. Electromagnetic radiation by antennas of arbitrary shape in a layered spherical media[J]. IEEE Tran- sactions on Antennas and Propagation, 2009, 57(12): 3827- 3834.

[5] Li L W, Kooi P S, Leong M S, Yeo T S. Electromagnetic dyadic Green‘s function in spherically multilayered media[J]. IEEE Transactions on Microwave Theory and Techniques, 1994, 42(12): 2302-2310.

[6] Khamas S K. Asymptotic extraction approach for anten- nas in a multilayered spherical media[J]. IEEE Transactions on Antennas and Propagation, 2010, 58 (3): 1003-1008.

[7] Tokgöz C and Dural G. Closed-form Green's Functions for Cylindrically Stratified Media[J]. IEEE Trans Microw Theory Tech, 2000, 48(1):40-49.

[8] 胡梦中, 尹成友, 宋铮, 熊俊卿. 圆柱分层介质中格林函数的完整求解Ⅰ:场型格林函数[J]. 微波学报, 2009, 25 (3): 1-6.

[9] 胡梦中, 尹成友, 宋铮. 圆柱分层介质中格林函数的完整求解Ⅱ:混合位格林函数[J]. 微波学报, 2009, 25(4): 11-15.

[10] 尹成友, 于涛, 唐伟. 球形分层媒质中并矢格林函数的求解I: 并矢格林函数的推导[J]. 微波学报, 2014, 30(3): 9-14.

[11] 于涛, 尹成友. 球形分层媒质中并矢格林函数的求解II: 并矢格林函数快速计算[J]. 微波学报, 2014, 30(4): 20-24.

[12] 于涛, 尹成友. 球状微带天线分析中细条带馈电模型的构建[J]. 系统工程与电子技术. 2014, 36(9): 1712-1716.

[13] 于涛, 尹成友, 刘汉. 基于特征基函数的球面共形微带天线阵列分析[J]. 物理学报, 2014, 63(23): 230701-1:7.

[14] He M and Xu X W. Closed-form solutions for analysis of cylindrically conformal microstrip antennas with arbitrary radii[J]. IEEE Trans. Antennas Propogat, 2005, 53(1): 518- 525.

作者：尹成友 于涛，电子工程学院，安徽合肥

来源：《2015年全国微波毫米波会议论文集》