学个Antenna是以天线仿真和调试为主,理论原理为辅的干货天线技术专栏,包括天线入门知识以及各类天线的原理简介、仿真软件建模、设计、调试过程及思路。如有想看到的内容或技术问题,可以在文末给我们留言。
摘要:天线和射频电路的端口匹配性能都调试合格,那么两者级联后的有效传输系数就一定良好么?答案是不一定,本期推文就谈谈天线设计中的负载牵引。
什么是阻抗匹配
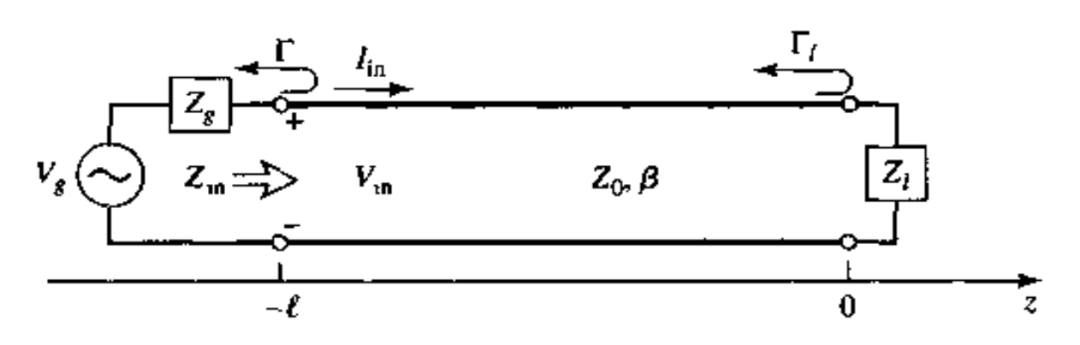
阻抗匹配是射频(RF)设计和测试的基本指标,对于一个射频收/发机而言,阻抗不匹配会导致不连续处的能量发生反射,阻碍电磁能量向外辐射。下图展示了一个典型的源和负载失配的传输线电路。
其中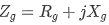 ,
,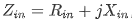 ,此时传到负载上的功率可表达为:
,此时传到负载上的功率可表达为:
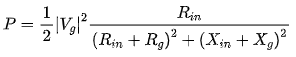
-
对于负载和传输线完全匹配的情况
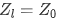 ,则传到负载上的功率为:
,则传到负载上的功率为:
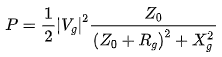
此时负载与传输线连接处的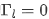 ,但是传输线与激励源连接处的
,但是传输线与激励源连接处的 不一定为0;
不一定为0;
-
若通过调整负载和传输线参数,使得,则传到负载上的功率为:
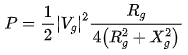
此时的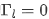 ,但是负载与传输线连接处的
,但是负载与传输线连接处的 不一定为0;
不一定为0;
-
对于固定源的串联阻抗,当满足共轭匹配
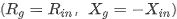 的时候,传输到负载的功率才能达到最大值:
的时候,传输到负载的功率才能达到最大值:
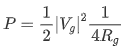
-
共轭匹配的时候虽然负载和源与传输线连接处的反射系数都不一定为0,但是失配线上多次反射的功率可能同相叠加,使得传输到负载的功率可能要大于传输线上无反射时传输的功率。
等反射系数圆
在讲负载牵引前,我们先介绍下Smith圆图中的等反射系数圆。教材上一般介绍并详细推导复平面上的归一化电阻圆和归一化电抗圆的公式,那么你知道等反射系数圆的公式怎么推导吗?
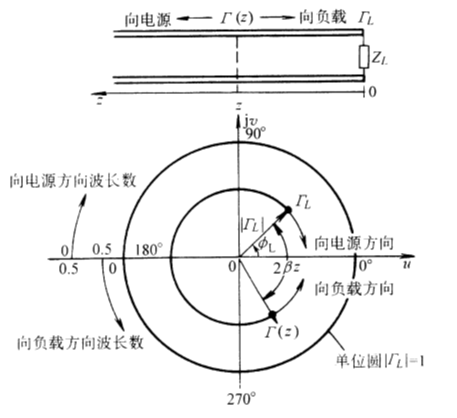

假设参考阻抗为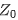 ,天线的输入阻抗为
,天线的输入阻抗为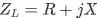 ,令天线始端看向激励端口(端口阻抗为
,令天线始端看向激励端口(端口阻抗为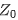 )端面处的反射系数为
)端面处的反射系数为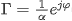 (等反射系数意味着其模值为常数,相位可变),则有下式成立:
(等反射系数意味着其模值为常数,相位可变),则有下式成立:
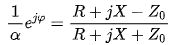
假设经过化简、整理可得,
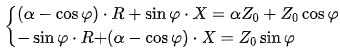
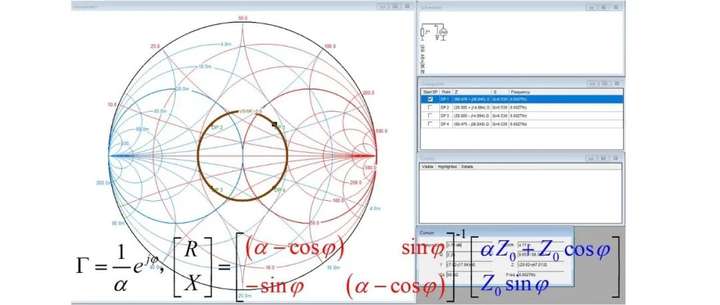
经过矩阵运算后可得,在等反射系数的约束条件下,天线的输入阻抗实部R和虚部X需要满足下面条件:
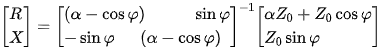
考虑VSWR=2,参考阻抗Z0=50Ω的情况,利用Matlab求解绘制等反射系数圆的阻抗分布图如下:
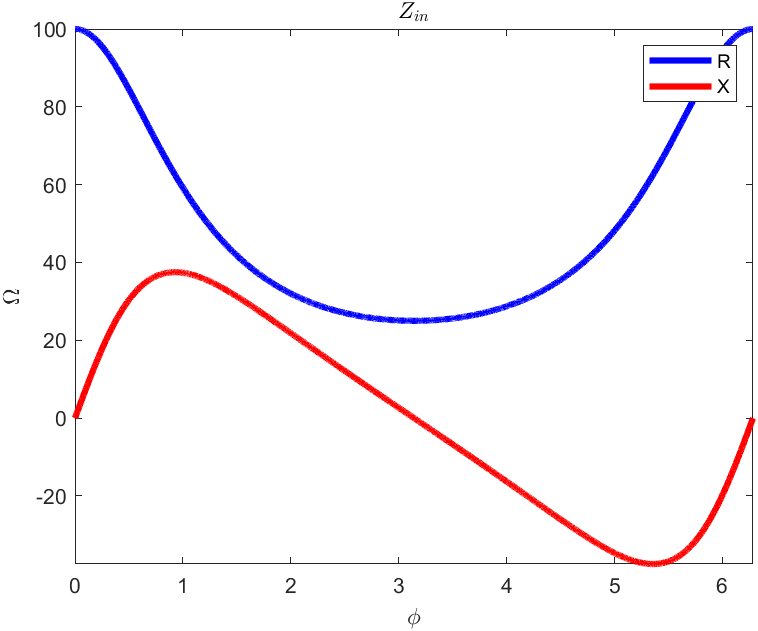
若是在复平面下绘制阻抗实部和虚部的关系图,就会发现该曲线就是圆,这是为什么呢?
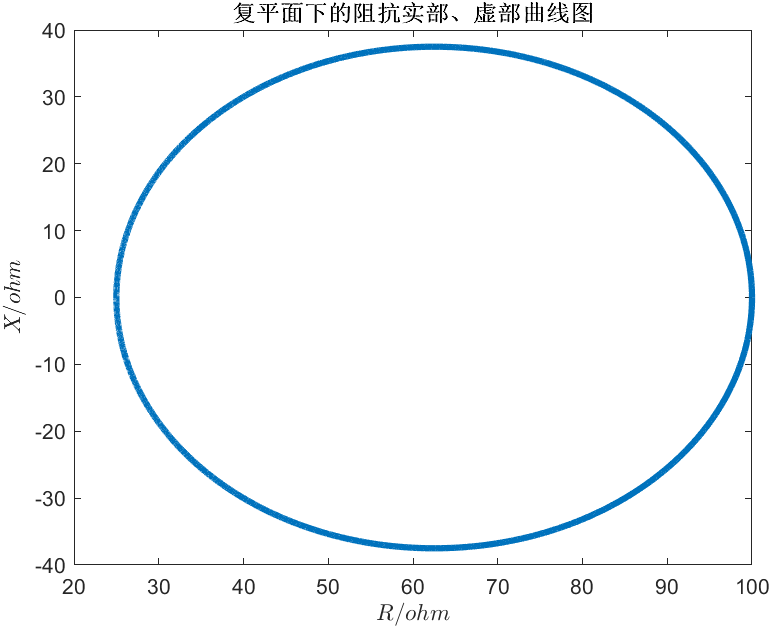
在复平面下,若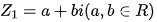 ,
,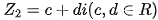 分别对应点
分别对应点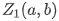 ,
,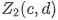 则:
则:
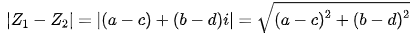
 表示两点
表示两点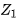 、
、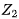 之间的距离,也等于
之间的距离,也等于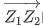 的模。
的模。
从复数平面上来看,重新观察下面式子,不难发现其几何含义:一动点(R,X)到定点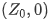 和
和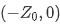 的距离之比为定值。
的距离之比为定值。
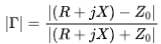
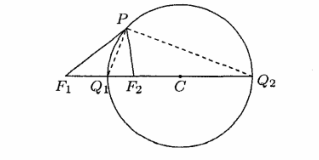
根据圆锥曲线的相关概念可知:动点到两定点的距离之和为定值,动点的轨迹曲线为椭圆;动点到两定点的距离之差为定值,动点的轨迹曲线为双曲线。那么动点到两定点的距离之比为定值时,动点的轨迹是什么呢?答案是圆。
设 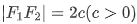 ,以线段
,以线段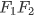 的中点
的中点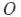 为原点,
为原点,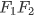 所在直线为
所在直线为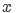 轴建立直角坐标系, 则
轴建立直角坐标系, 则、
,设动点
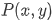 ,由
,由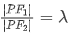 得:
得:
当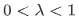 时, 方程化为:
时, 方程化为:
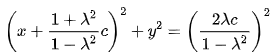
其表示以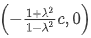 为圆心,
为圆心,  为半径的圆;
为半径的圆;
当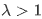 时,方程化为:
时,方程化为:

其表示以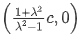 为圆心,
为圆心, 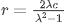 为半径的圆
为半径的圆
将上面的反射系数公式改写如下:
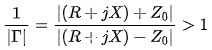
因为前文令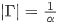 ,易得动点(R,X)的轨迹曲线是圆心为
,易得动点(R,X)的轨迹曲线是圆心为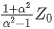 ,半径为
,半径为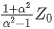 的圆。带入VSWR=2,参考阻抗Z0=50Ω的条件,可得圆心为(62.5,0),半径为37.5。
的圆。带入VSWR=2,参考阻抗Z0=50Ω的条件,可得圆心为(62.5,0),半径为37.5。
天线设计的负载牵引现象
当射频和天线端都按照50Ω作为参考阻抗,VSWR≤2进行调试,那么天线的输入阻抗或射频末端的视入阻抗将落在等反射系数圆内。虽然用矢网单独测试天线或者射频电路,其匹配性能达标,但是两者级联时端口的不连续性可能恶化,这就是一种负载牵引现象。
有了前文的铺垫后,考虑最简情况进行计算说明。在等反射系数圆上每个象限取一点:DP1、DP2、DP3、DP4这四个点。
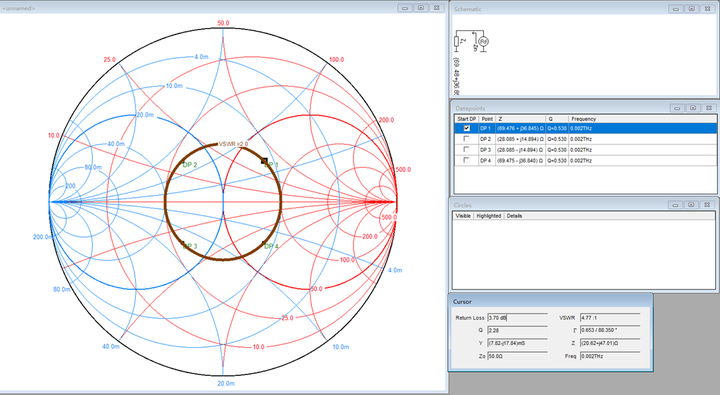
假设DP1为天线端的输入阻抗,对于射频端分别取DP2,DP3,DP4三点,计算从射频端到天线端视入的端口反射系数如下:
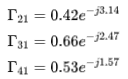
因为天线和射频端口的驻波比均小于2,也就是反射系数小于0.33,但是两者级联后,三种不同情况下的连接处反射系数均大于0.33。为了解决这个问题,可以在天线端和射频端插入一段50Ω传输线。如果射频端的阻抗点为DP3,考虑到最大功率传输的情况是需要共轭匹配,因此可以将其天线的端口阻抗DP1顺时针旋转至DP3的共轭阻抗处,即DP2点。
当然了,工程上来讲匹配的频段往往较宽,如果不是特别影响整机发射功率,其实不用这么精确地进行最大功率传输的设计。例如对于IPEX线馈电的套杆天线,可选择不同线长的IPEX线进行整机性能测试,最后选择较优线长。

以上便是要给大家分享的内容,希望对大家有所帮助~~
-END-
作者:94巨蟹座少年
大家持续关注“微波射频网”,后续精彩不断~
本文为MWRF.NET原创文章,未经允许不得转载,如需转载请联系market#mwrf.net(#换成@)

 粤公网安备 44030902003195号
粤公网安备 44030902003195号