零基础入门智能射频——基于泰勒综合法的PYTHON与HFSS联合仿真阵列天线设计

1 前言

前篇介绍了切比雪夫综合法得到低副瓣特性的阵列天线，由上篇分析可知，等幅激励的均匀线阵的副瓣电平幅度较高，可使用切比雪夫综合法、泰勒综合法实现阵列天线的方向图低副瓣特性。当天线的阵元个数超越一定范围时，切比雪夫的两端的电流差距很大，阵列天线两端的单元会发生突然的跳变的现象，影响天线的低副瓣效果。因此，切比雪夫综合法在某些雷达系统中并不是很适用，为了解决这一问题，下面将介绍泰勒综合法。

图 1阵列天线自动设计

2 基于泰勒综合法的均匀阵列

泰勒综合法是实现低副瓣阵列天线的一种方法，具有副瓣电平可控的特性，并且由于副瓣的递减特性不会出现切比雪夫综合法里面两端突然跳变的现象，降低馈电网络设计的复杂度，并且还会增强天线的方向性在工程上得到了广泛的认可。辐射特性具有如下特点：

1. 主瓣两侧的若干副瓣电平大小相似；
2. 其余区域副瓣电平会单调减小。

由以上特点可知，阵列天线的激励从中间往两侧会单调递减，不会发生切比雪夫综合法中的跳变现象，方向图函数为：

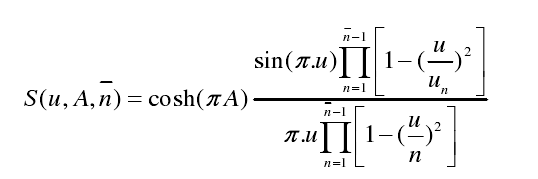
上式为构造的泰勒空间因子，具有理想空间因子可调副瓣电平和前n-1个副瓣电平接近相等的性质，同时在远区副瓣保持了基本函数的副瓣峰值，也具备μ^-1的衰减特性。其零点位置为：

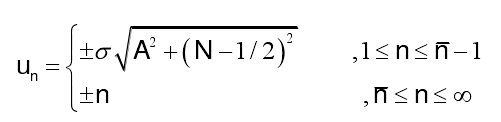
式中，

1）若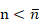时，副瓣可称为近旁瓣，近似相等；反之副瓣称为远旁瓣，逐渐衰减，。上式的u取整数时，即为方向图零点位置。

2）若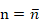时，零点重合，有下式：

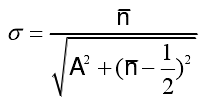
当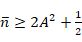时，得到的阵列方向图函数即为：

令天线阵列馈电幅度分布为I(ξ)，其具有的泰勒分布如下图所示。

a) 泰勒连续分布

泰勒连续分布示意图如图 1所示。

图 2 泰勒分布示意图

对应的连续电流分布为：

其中，k_ξ表示均匀相位常数，α(ξ)是非均匀相位常数，由上图可知，电流分布具有对称性，则该分布对应的阵列单元辐射阵因子为：

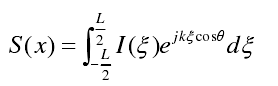
1. X=i=0时，泰勒方向图函数 S(x)=1；
2. X=i小于n时，S(x)为：

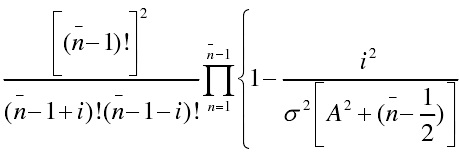
3. X=i大于n时，S(x)=0。
4. 口径场分布函数I(ξ)为：

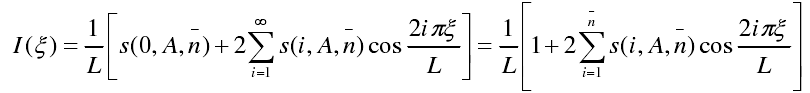
b)离散化

对于线阵而言，需要对上图进行离散化，每个抽样值对应着直线阵列上的单元激励，利用抽样定理，可以增加抽样点使阵列单元的对应的幅度分布来贴合泰勒分布的连续线源幅度。

离散化后，每个阵元的坐标位置为：

各单元对应的激励电流幅度为：

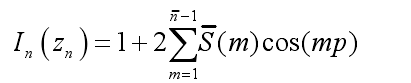
式中，p=2Πz_n/L，L=Nd

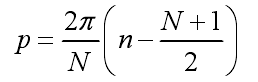
这里的，S(m)为：

1. m=0时，泰勒方向图函数 S(m)=1；
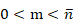2. 时，S(m)为：

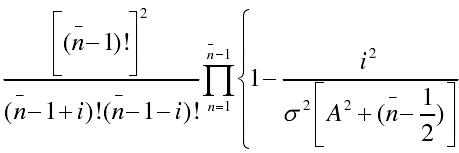
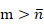3. 时，S(m)=0。

该式说明，对泰勒线源进行抽样时，抽样结果只与抽样点数相关，可以看出激励幅度与单元数量有关，而和单元间距无关。

3 联合仿真分析

1.阵元数不变，调整阵间距

对于20阵元的天线，分别仿真了间距为λ、λ/2、λ/4情况下的辐射特性，如下图所示。三种情况下的天线阵元激励幅度相同。

单元数为20，阵元间距d为λ，指向0度

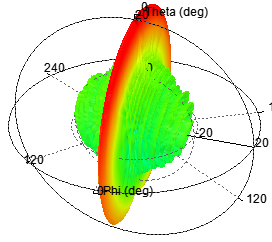
单元数为20，阵元间距d为λ/2，指向0度

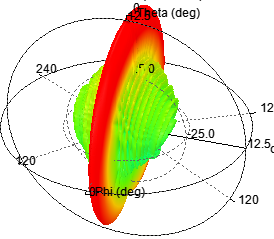
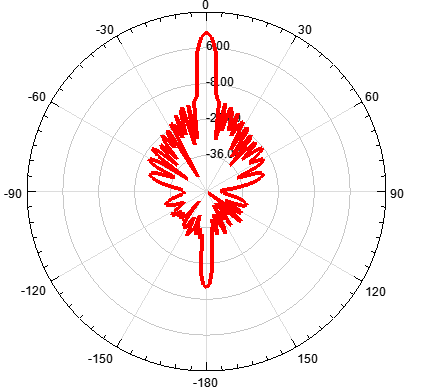
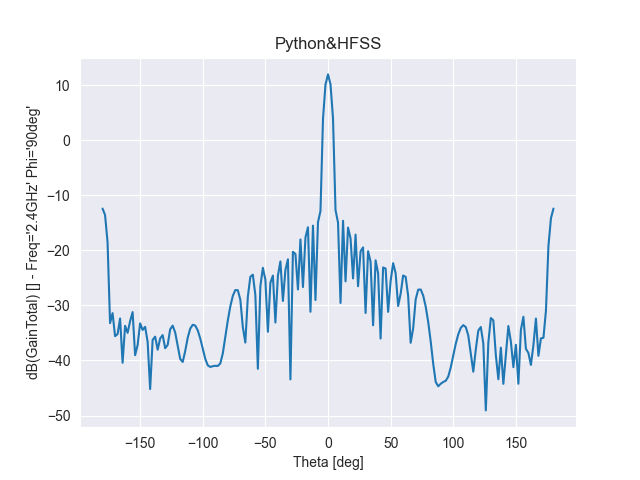
图 3 d=λ/2辐射特性

单元数为20，阵元间距d为λ/4，指向0度

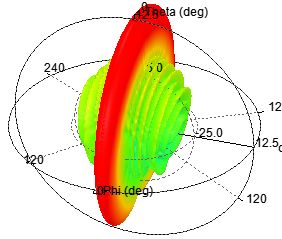
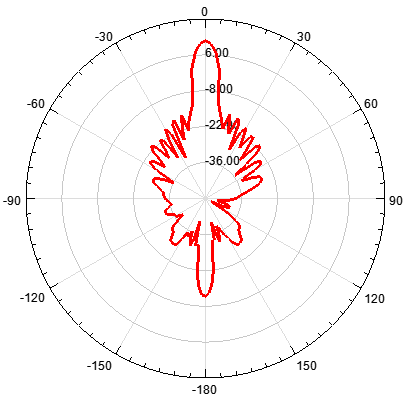
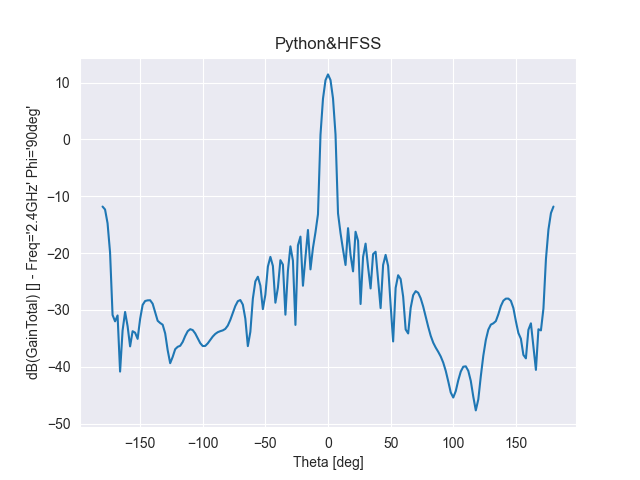
图 4 d=λ/4辐射特性

2.切比雪夫综合与泰勒综合对比

下面通过python与HFSS设计了两组12元阵天线，分别采用了切比雪夫综合法和泰勒综合法，对比说明两者的不同之处。

基于切比雪夫综合法，单元数为12，阵元间距d为λ/2，指向0度

 

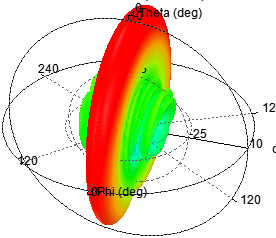
图 5 切比雪夫综合法得到的辐射特性

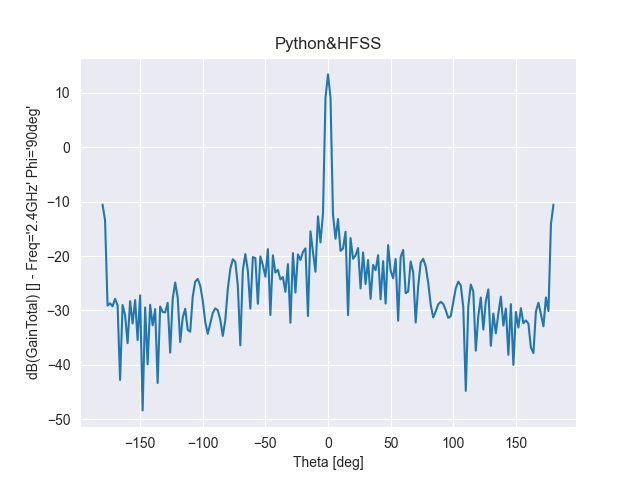
基于泰勒综合法，单元数为12，阵元间距d为λ/2，指向0度

 

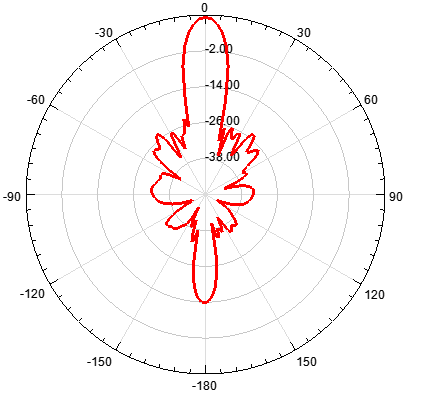
图 6 泰勒综合法得到的辐射特性

两者对比情况

通过对比可知，切比雪夫综合方法的阵列天线副瓣幅度一致；泰勒综合法的随着角度逐渐偏离主瓣，副瓣电平逐次递减；其次，单元太少则达不到预设值。

4 小结

由上述分析可知，

1.切比雪夫综合方法的阵列天线副瓣幅度一致；泰勒综合法的随着角度逐渐偏离主瓣，副瓣电平逐次递减；

2.阵元数大于13时，适用泰勒综合法；

3.单元太少则达不到预设值。

作者：江右射频