零基础入门智能射频(四)—— PYTHON与HFSS联合仿真之阵列天线设计（二）

1 前言

前篇介绍了阵列天线的基础，以十元阵为例，使用Python和HFSS自动化建模并进行了仿真，快速准确地研究分析了天线阵辐射特性随着阵元间距的变化而变化的情况。

2 基于切比雪夫综合法的均匀阵列

由上篇分析可知，等幅激励的均匀线阵的副瓣电平幅度较高，为了解决这一问题，可使用切比雪夫综合法、泰勒综合法实现阵列天线的方向图低副瓣特性。

这里先介绍切比雪夫综合法得到低副瓣特性的阵列天线。

P阶切比雪夫多项式如下：

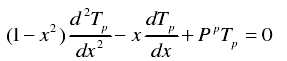
当p为偶数时 ，Tp见下式：

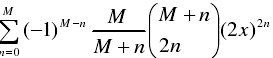
当p为奇数时 ，Tp见下式：

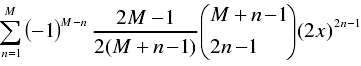
其中的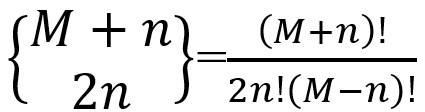

当天线的波瓣特性和切比雪夫多项式曲线一致时，该天线辐射特性具有切比雪夫特性，此时旁瓣的幅度都均相等。

由上式可知，当阵列单元为偶数阶时，其阵因子如下：

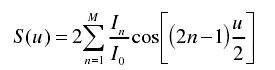
当阵列单元为奇数阶时，其阵因子如下：

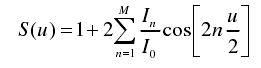
式中，。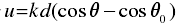

依据单元数为奇偶分以下情况得到对应的电流幅度。

a) 对于单元数为奇数的阵列

对于单元数为奇数的阵列而言，中心单元的激励幅度为：

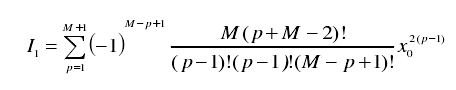
其一侧的相对单元激励幅度为：

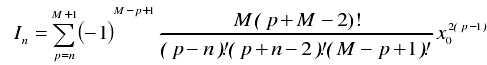
b) 对于单元数为偶数的阵列

其一侧的相对单元激励幅度为：

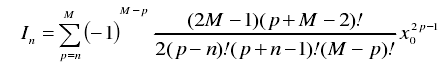
下面借助联合仿真快速分析切比雪夫综合法得到的阵列天线辐射特性，使用python实现从切比雪夫综合法计算到HFSS自动化设计全过程。

 

3 联合仿真分析

3.1 阵元数不变，调整阵间距

      a)单元数为10，阵元间距d为λ/2，指向30度

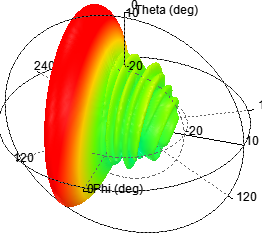
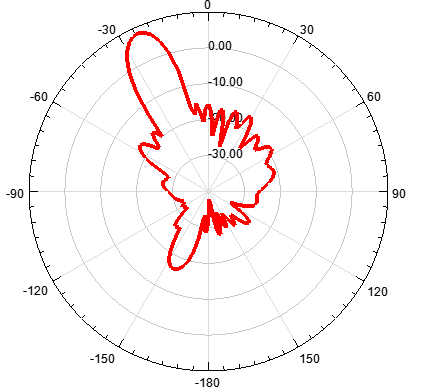
      b)单元数为10，阵元间距d为λ/4，指向0度

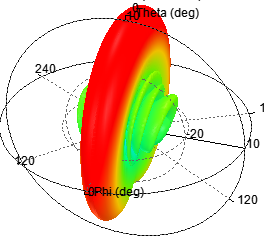
      c)单元数为10，阵元间距d为0.3λ，指向0度

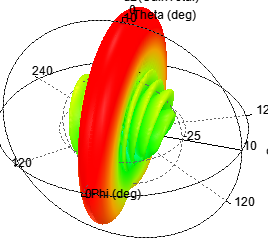
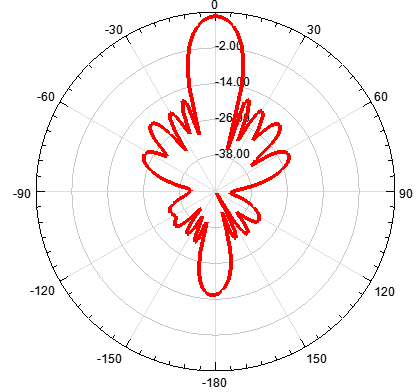
      d)单元数为10，阵元间距d为λ/2，指向0度

 

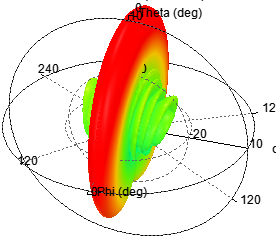
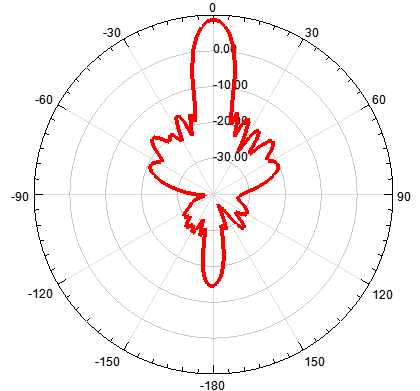
      e)单元数为10，阵元间距d为λ，指向0度

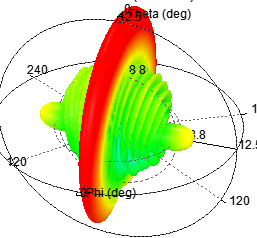
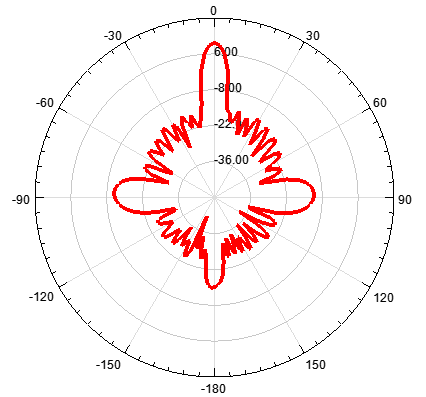
可见，当阵元间距d增大时，副瓣会增多，同时副瓣变的尖锐。

3.2 间距不变，调整阵元数

      a)单元数为12，阵元间距d为λ/2，指向0度

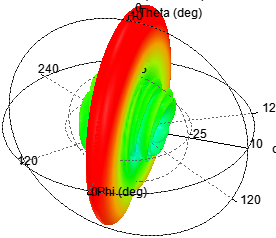
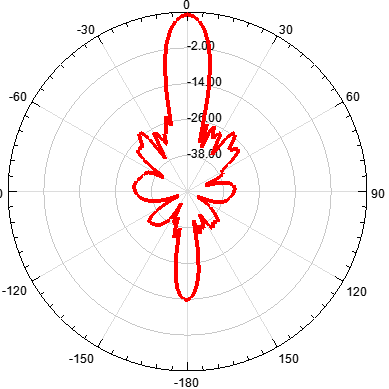
      b)单元数为10，阵元间距d为λ/2，指向0度

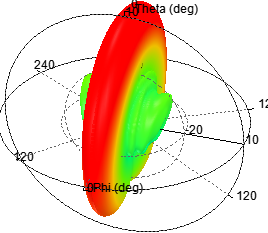
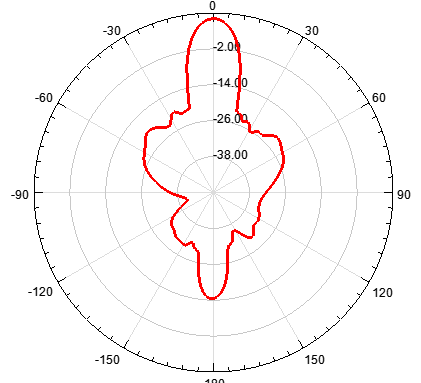
      c)单元数为6，阵元间距d为λ/2，指向0度

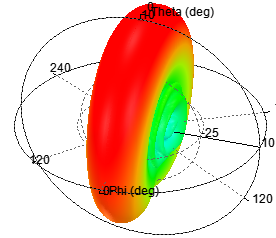
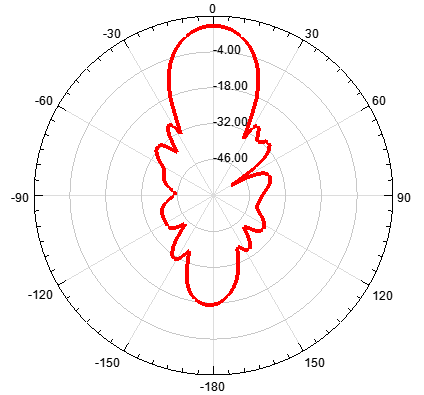
可见，当N值增大时，辐射的方向性加强，方向图越尖锐。

4 小结

由上述分析可知，

      a)当阵元间距d增大时，副瓣会增多，同时副瓣变的尖锐；

      b)当N值增大时，辐射的方向性加强，方向图越尖锐；

      c)由于切比雪夫分布所有的旁瓣电平都相等，将分散一部分功率，使得天线的增益降低。