1 前言
前面介绍了PYTHON与HFSS联合仿真LPDA系列,认识了常见的LDPA天线形态,学习了LPDA的基本设计方法,最后总结关于LPDA天线的特点和注意事项,这些知识点有助于工程师能力的提高。
从本节起,将开启一个阵列天线系列,陆续介绍基础理论知识、PYTHON与HFSS联合仿真阵列天线。

图 1 阵列天线自动建模
2 阵列天线种类
2.1 概述
阵列天线是一类由不少于两个天线单元规则或随机排列并通过适当激励获得预定辐射特性的特殊天线。
2.2 阵列天线分类
a)阵列天线按照排布方式可分为以下几类:
a1 线性阵列
a2 平面阵列
a3 立体阵列
a4 圆形阵列

图 2 阵列天线分类1
b)阵列天线按照辐射图可分为以下几类:
b1 侧射天线阵
b2 端射天线阵
b3 既非侧射又非端射的天线阵
侧射天线阵是最大辐射方向指向阵轴或阵面垂直方向的天线阵;端射天线阵是最大辐射方向指向阵轴方向的天线阵;最大辐射方向指向其他方向的天线阵为双非既非侧射又非端射的天线阵。

图 3 阵列天线分类2
c)阵列天线按照功能可分为以下几类:
c1 同相水平天线
c2 频率扫描天线
c3 相控阵天线
c4 多波束天线
c5 信号处理天线
c6 自适应天线
3 均匀线阵联合仿真分析
3.1 线阵方向图分析
阵列天线可由下列四个参数确定其天线的辐射特性:
a.单元数目
b.单元间距
c.各单元的激励幅度
d.各单元的相位分布
现有一线阵由N各相同单元组成,各个单元间距为d,并且各单元激励电流幅度相等,各相邻单元的馈电相位差都为β构成了均匀直线阵。
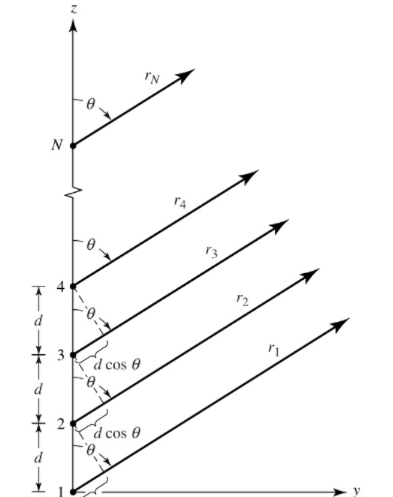
图 4 线阵天线
如图所示,来波位于θ方向,参考波前面定义为零相位,对于不同的单元均对应的相位βn,这里激励幅度相同,归一化为1, 此时该天线阵的阵因子为:
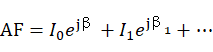
简化分析,对于一个间距为一个波长的二元线阵而言, 沿X轴场强同相得到加强,顺时针旋转此时各处的相位差将从0变化至360°,此时相位差可表示为d cosθ,这里d=λ。
当θ为60°和120°时,cosθ=0.5,即将出现半波程意味着将产生一个零点;同理,θ为90°,此时场强加强。此时远场图如下图所示。
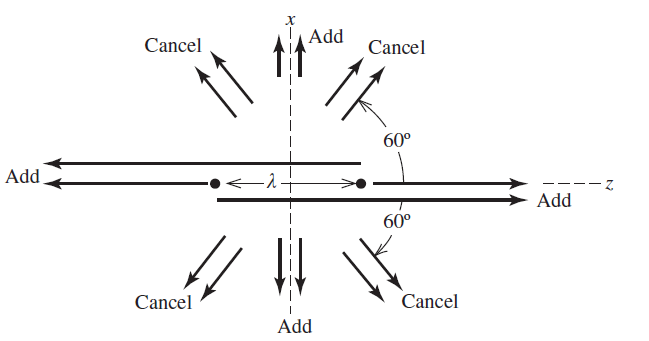
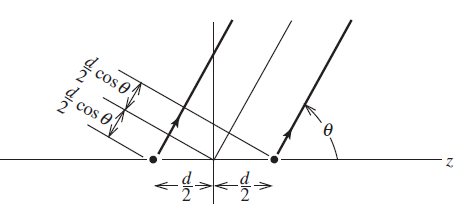
图 5 二元线阵
接着推导一下阵因子,其为两单元之和,即
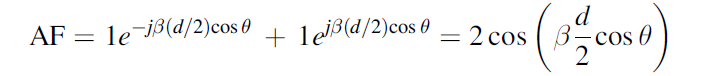
将d=λ带入上式得到:
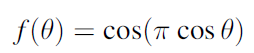
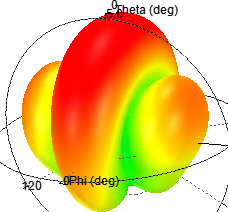
图 6 二元阵辐射特性
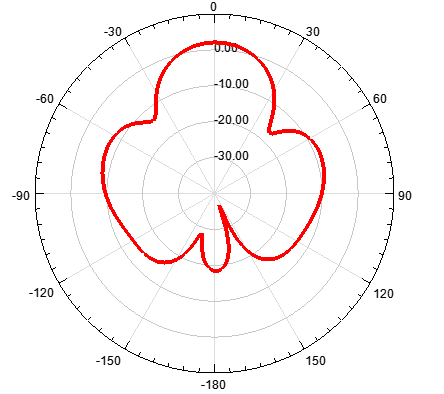
图 7 二元阵方向图
推广至N元阵,相邻单元接收到的信号的相位差为φ=2Πd/λsinθ,则均匀直线阵的远区辐射场表达式为:
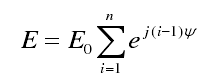
均匀直线阵的阵因子为:
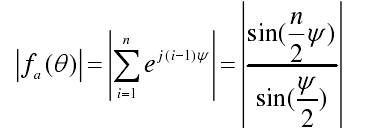
当已知各相邻单元的馈电相位差β时,由上式可知,阵因子f(θ)是周期为2Π的函数。同时波瓣最大值会随之重复出现,当ψ=0时,阵因子将出现主瓣的最大值,波束指向见下式:
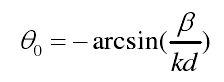
当θ=90时,波束指向与阵轴垂直,线性阵列为侧射阵。当θ=0时,波束指向在阵轴方向,线性阵列为端射阵。当需要波速指向特定角度时,则按照该公式可求出各个阵元间的相位差。
阵列天线的建模、结果数据分析代码如下:
Hfssstart()
arrayant(2400,4.3,0.8,10)
Save()
Analyze()
ResulteSave()
这里调用了作者封装的函数,arrayant根据计算的参数建立天线模型,过程如下图所示。

图 8 联合仿真设计
3.2 线阵联合仿真分析
借助上节自动建模程序,本节从全波电磁仿真角度出, 分为三小节讨论等幅激励线阵天线的辐射特性。
a)不同阵元等间距
五元线阵当其间距为2λ/3时,由Python和HFSS联合仿真结果如下:
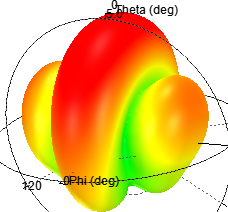
图 9 5阵元合成辐射图
二十元线阵当其间距为2λ/3时,由Python和HFSS联合仿真结果如下:
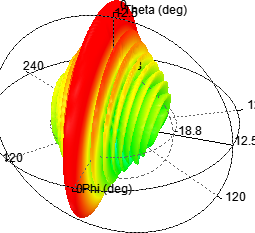
图 10 20阵元合成辐射图
通过两者对比,阵列天线的单元数越多,其波束越窄,指向性明显。
b)相同阵元不同间距
十元线阵当其间距为λ时,由Python和HFSS联合仿真结果如下:
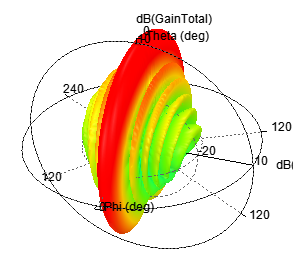
图 11 10阵元合成辐射图
十元线阵当其间距为λ/2时,由Python和HFSS联合仿真结果如下:
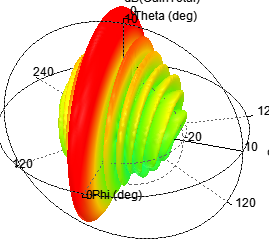
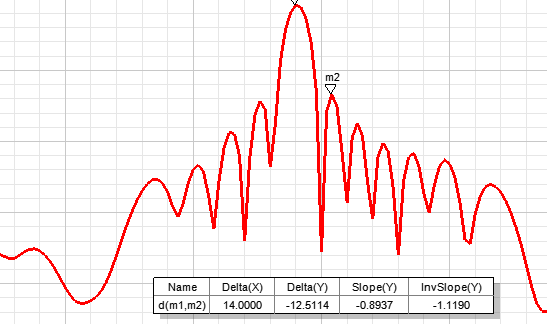
图 12 间距为λ/2方向图
十元线阵当其间距为λ/4时,由Python和HFSS联合仿真结果如下:
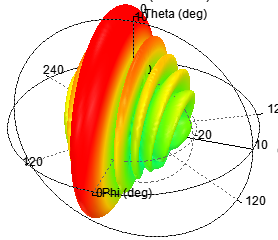
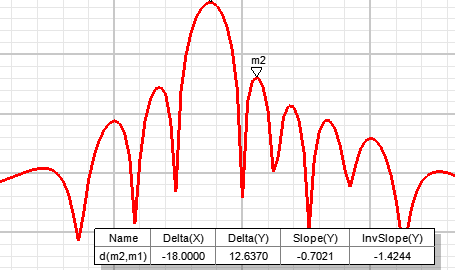
图 13 间距为λ/4方向图
c)相同阵元相同间距不同综合方法
等幅激励的十元线阵当其间距为λ/2时,由Python和HFSS联合仿真结果如下:
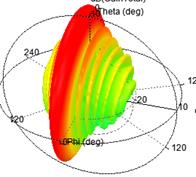
图 14 等幅激励
同样十元线阵采用切比雪夫综合法得到的联合仿真结果如下:
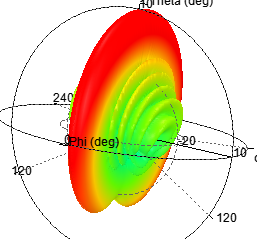
图 15 切比雪夫综合法
对比两者辐射图,切比雪夫综合法得到的各个单元激励幅度不同,最终合成的方向图主副瓣比改善显著。

 粤公网安备 44030902003195号
粤公网安备 44030902003195号