阵列天线的赋形波束综合(二)---伍德沃德—劳森抽样法

学个Antenna是以天线仿真和调试为主，理论原理为辅的干货天线技术专栏，包括天线入门知识以及各类天线的原理简介、仿真软件建模、设计、调试过程及思路。如有想看到的内容或技术问题，可以在文尾写下留言。

摘要：

在上次关于阵列天线赋形波束综合推文——阵列天线的赋形波束综合(一)中，对傅里叶级数法进行简单的公式阐述和CST实例验证。本次推文则献上伍德沃德—劳森抽样法实例。

本文使用的软件为CST 2018和MATLAB 2019A

伍德沃德—劳森抽样法

伍德沃德—劳森抽样法需要通过对给定方向图的不同离散角度进行抽样。看到这很多人就开始想，这咋感觉想信号与系统里面的那玩意，还抽样了？上次讲傅里叶级数法求解给定单元的激励幅度来实现期望方向图也很像时域-频域变换。专业课最后还是靠数学作为最后的求解工具，数学——YYDS！

回顾下在浅谈阵列天线及布阵中的一堆公式(左右滑动看完整公式)：

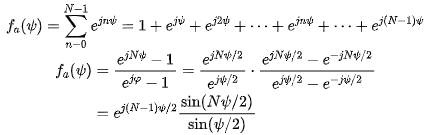
上面这个阵因子叠加公式，其实就能从中推出均匀直线阵的第一副瓣值和角度位置，各零点角度位置，线阵单元相差与波束指向的关系，主瓣3dB波束等参量。

当上面最简单的等幅同间矩的直线阵改为下面这种等间距，幅相均可变的直线阵后，所能综合的远场方向图自由度就提高了。

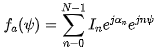
也是在这种约束条件下，Woodward在下面两篇论文中阐述伍德沃德—劳森抽样法的原理，这也成为了一种非常流行的用于任意波束赋形的天线方向图合成方法。

1. P. M. Woodward, “A Method for Calculating the Field over a Plane Aperture Required to Produce a GivenPolar Diagram,” J. IEE, Vol. 93, pt. IIIA, pp. 1554–1558, 1946.

2. P. M. Woodward and J. D. Lawson, “The Theoretical Precision with Which an Arbitrary Radiation-Pattern May be Obtained from a Source of a Finite Size,” J. IEE, Vol. 95, pt. III, No. 37, pp. 363–370, September 1948.

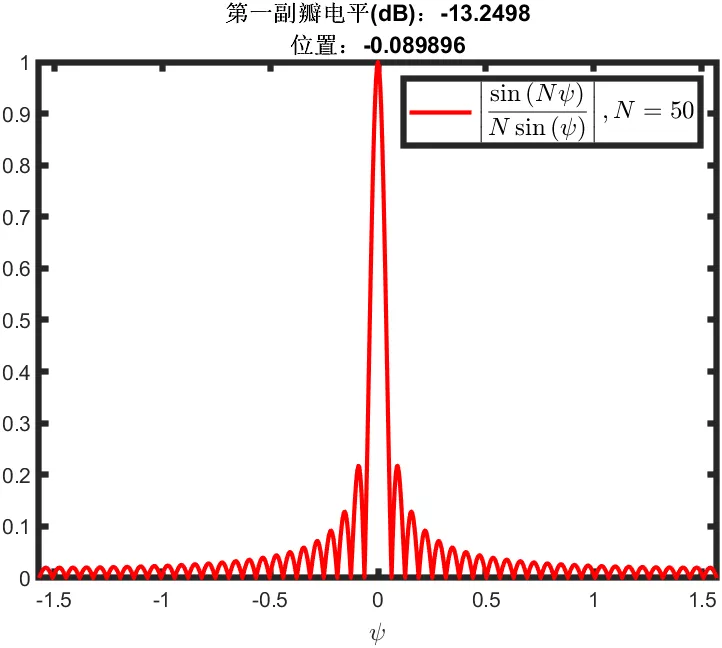
如何理解这种方法呢，最简单的思想就是：对于一个直线阵而言，一组不同的幅相配置会产生不同的波束指向。利用如下所示的方向图的3dB波束宽度去填充想要的目标方向图，将所有组方向图对应的幅相激励进行叠加，得出最后每个单元最终应该分配的幅度和相位。

例如对于下图这种方波似的目标方向图，用不同波束指向的方向图进行叠加。

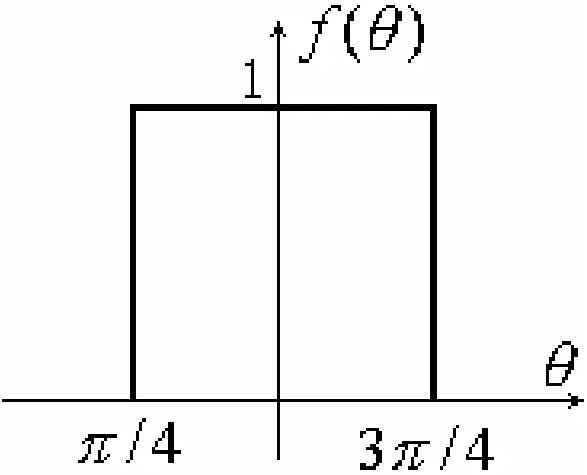
%matlab code clear;clc;N=10;format long; color_array={'r','g','b','m','k'}; theta0_array=45:10:135;legend_str={}; h=figure;set(gcf,'Position',[100 100 800 600]); for num=1:length(theta0_array)     theta=0:0.1:180;theta0=theta0_array(num);     F=abs(sin(N*deg2rad(theta-theta0))./(N*sin(deg2rad(theta-theta0))));     plot(theta,F,color_array{mod(num,length(color_array))+1},'linewidth',2);     set(gca,'linewidth',3);     xlabel('\theta(°)','Fontsize',12);     ylabel('F(\theta)','Fontsize',12);     set(gca,'XTick',0:10:180);     set(gca,'YTick',0:0.1:1);     axis([0,180,0,1]);     legend_str{num}=strcat(num2str(theta0),'°');     hold on; end h=legend(legend_str); set(h,'FontName','Times New Roman','FontSize',12,'FontWeight','normal'); hold off;

运行上面的Matlab代码，得出如下不同波束的叠加图，若是可以取其包络，那么采样点越多，带内的纹波越小。

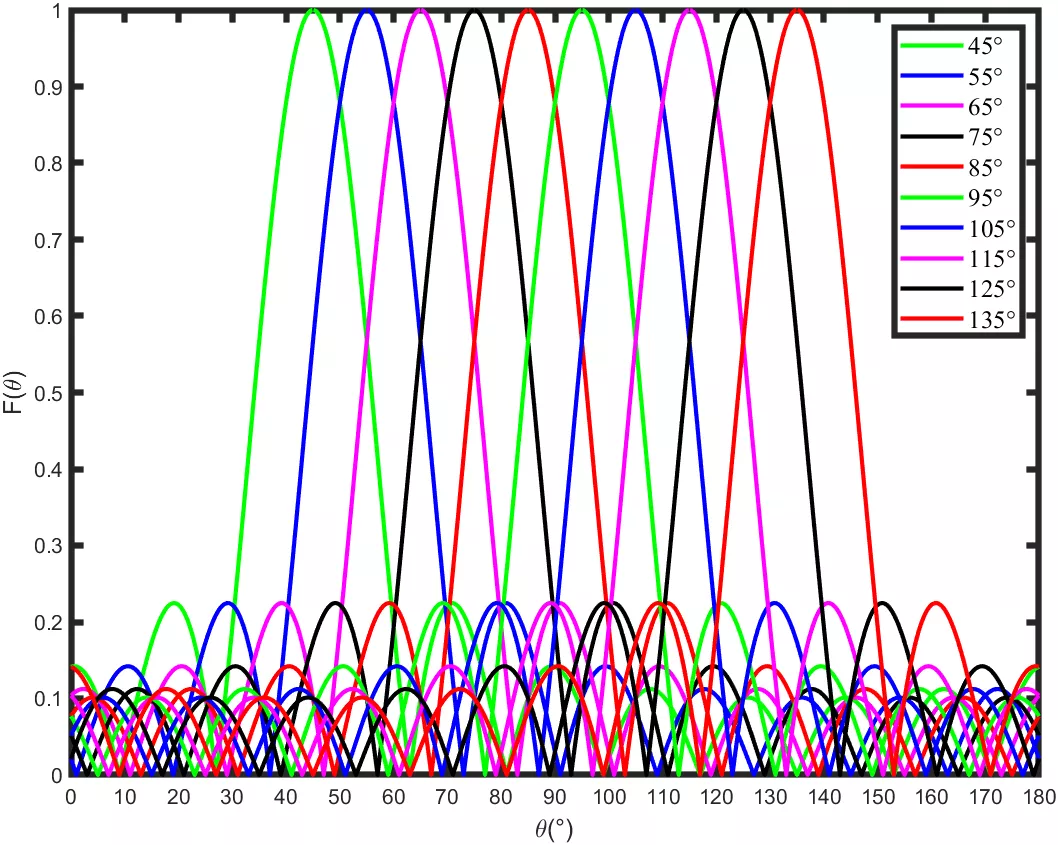
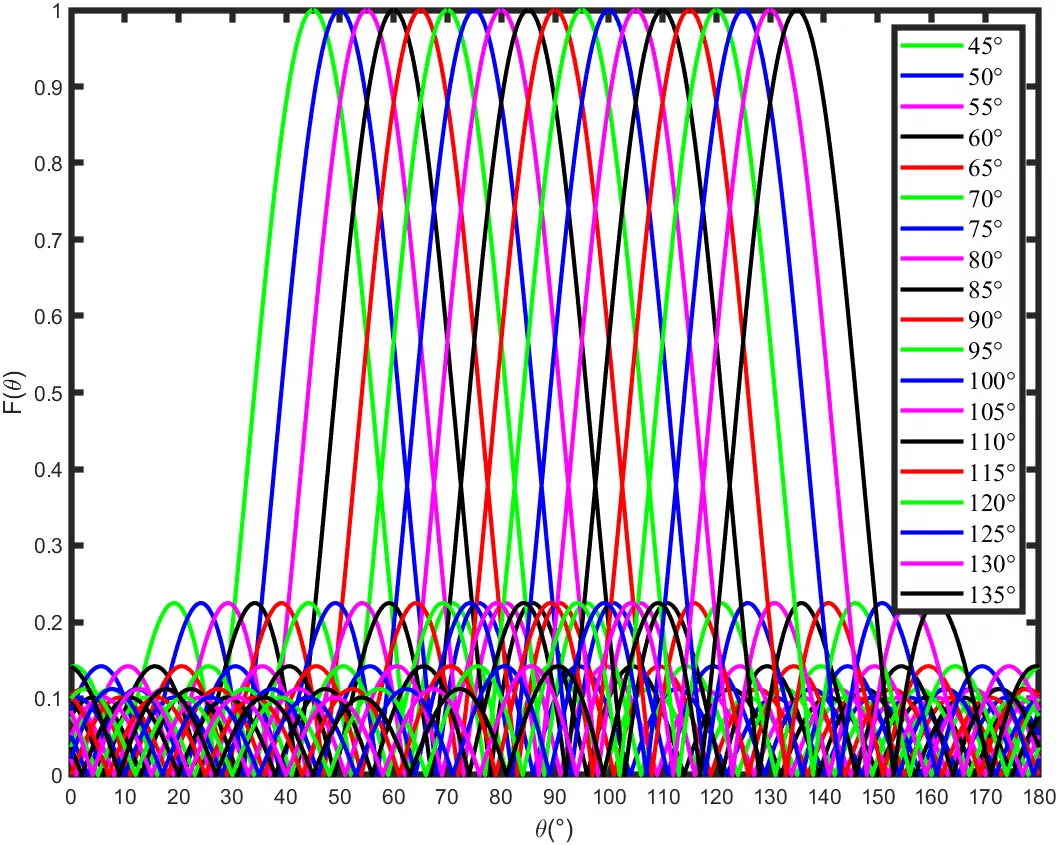
左图为采样间隔10°，右图为采样间隔5°

可实际上我们是要将这些方向图进行相加操作：

%matlab code clear;clc;N=10;format long; theta0_array=45:5:135; h=figure;set(gcf,'Position',[100 100 800 600]); Ftotal=0; for num=1:length(theta0_array)     theta=0:0.1:180;theta0=theta0_array(num);     F=abs(sin(N*deg2rad(theta-theta0))./(N*sin(deg2rad(theta-theta0))));     Ftotal=Ftotal+F; end F_uniform=Ftotal/max(Ftotal); plot(theta,F_uniform,'r','linewidth',2); set(gca,'linewidth',3); xlabel('\theta(°)','Fontsize',12); ylabel('Ftoal(\theta)','Fontsize',12); set(gca,'XTick',0:10:180); set(gca,'YTick',0:0.1:1); axis([0,180,0,1]);

于是就出现了下面的最终方向图：

看着还可以，不过伍德沃德—劳森抽样法没有我们那么想当然，一切完备的理论都需要用数学去描述它。

下面就直接进入本次推文的核心内容：

第一步，确定采样角度和激励系数。还是以上面那个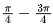内的类方波的期望方向图为例。假设直线阵的单元间距为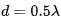，单元数为N=10，线阵长度。

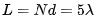为了使综合的方向图对应可见区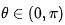，准确地重建给定的方向图，抽样间隔可确定为:

抽样角度可根据采样点数的奇偶性表达如下(左右滑动看完整公式)：

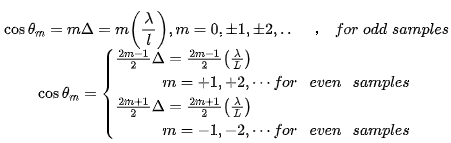
因此抽样角度可以通过上述公式计算得出，该角度对应的激励系数则取为期望方向图对应抽样角度处的值，若抽样点正好在预给的期望方向图的边界上，则抽样值取其一半。

clear;clc; lambda_d=0.2; for m=-5:1:5     theta_m=rad2deg(acos(m*lambda_d)); end

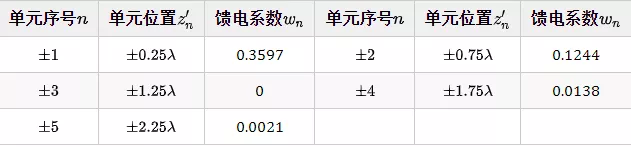
计算后得到如下表：

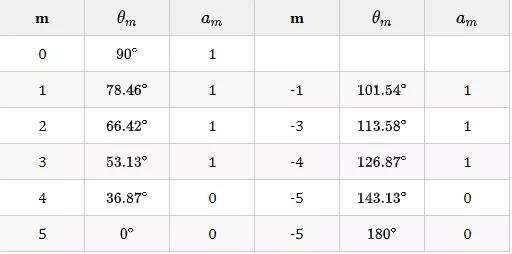
第二步，确定各单元的馈电系数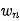。对于离散直线阵而言，各单元的馈电系数可由下式确定：

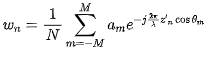
各单元的馈电系数如下所示：

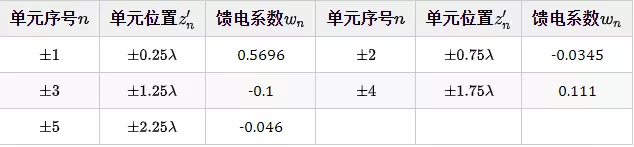
CST实例

将浅谈阵列天线及布阵的模型略微修改下，使其工作频率在15GHz附近，工作频率半波长为10mm，间隔半波长布置10个单元。

在CST CombineResults里将上节计算的馈电系数代入进去计算，可得15GHz的远场方向图如下：

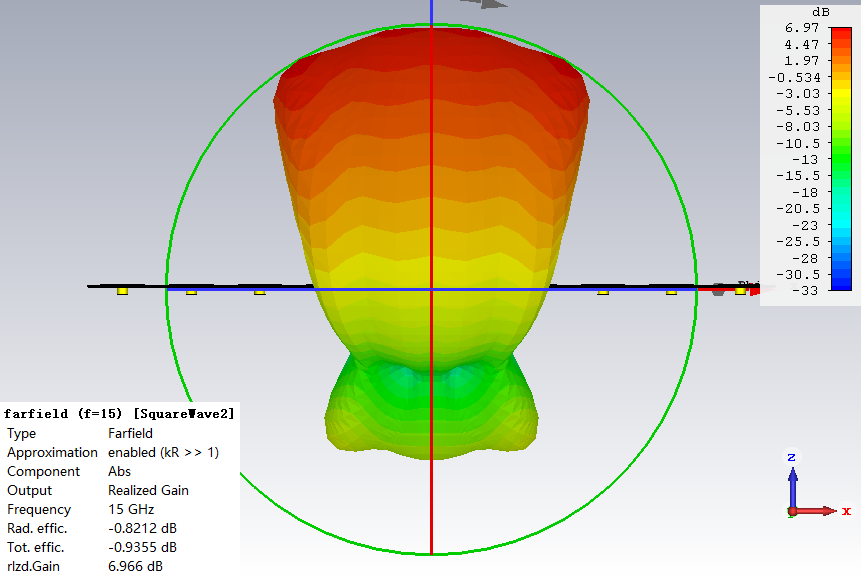
由于本次采用的10单元线阵去实现期望方向图，相较于阵列天线的赋形波束综合(一)单元数减半，因此可以看出中间部分的增益平坦度略微逊色。因为前面计算的阵列沿着轴排布，而上面的阵列是沿着轴组阵，因此看方向图时，加个就可，或者直接将下图的横坐标看成0~180°范围亦可。

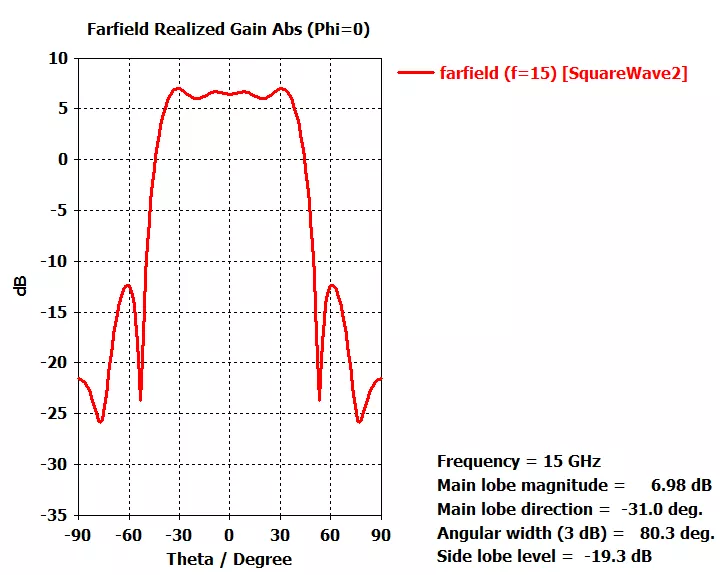
下图所示为20单元线阵下，利用傅里叶级数法综合的期望方向图：

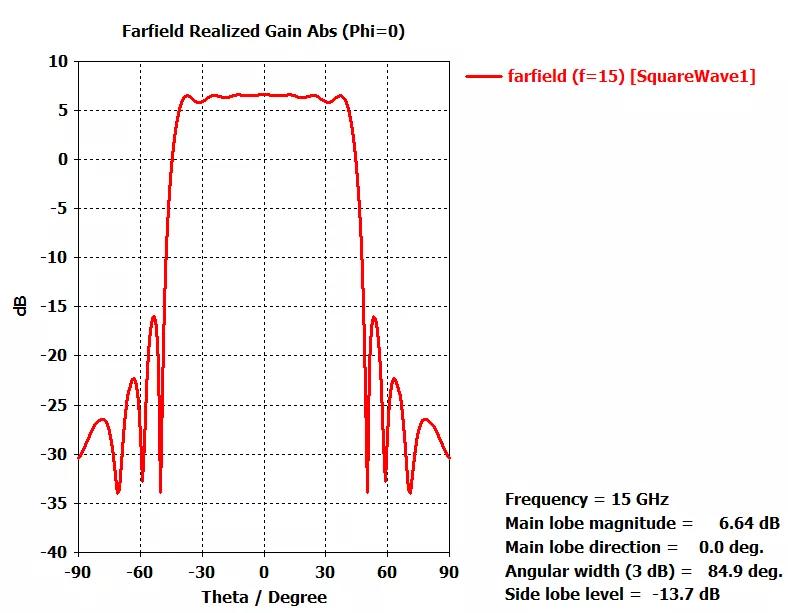
接下来分别综合了更宽波束的类方波方向图和宽波束笔状方向图：

类方波方向图-馈电系数

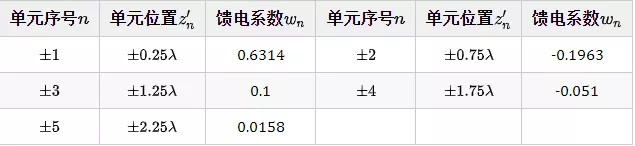
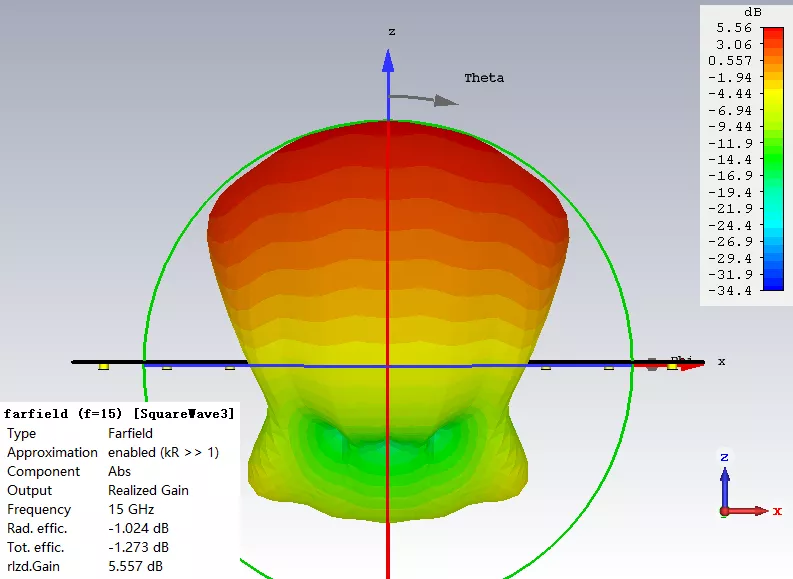
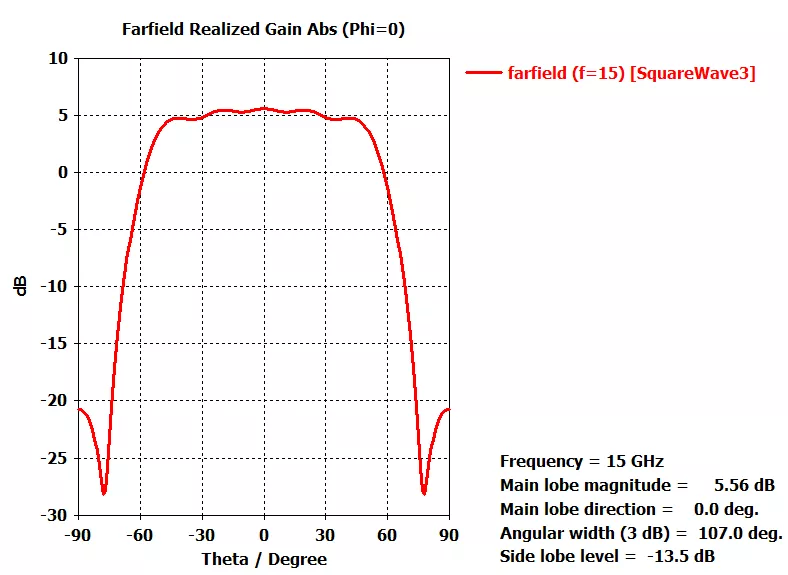
从上面的仿真结果可以看出，3dB波束宽度达到了107度，且带内增益平坦度不错。

宽波束笔状方向图-馈电系数

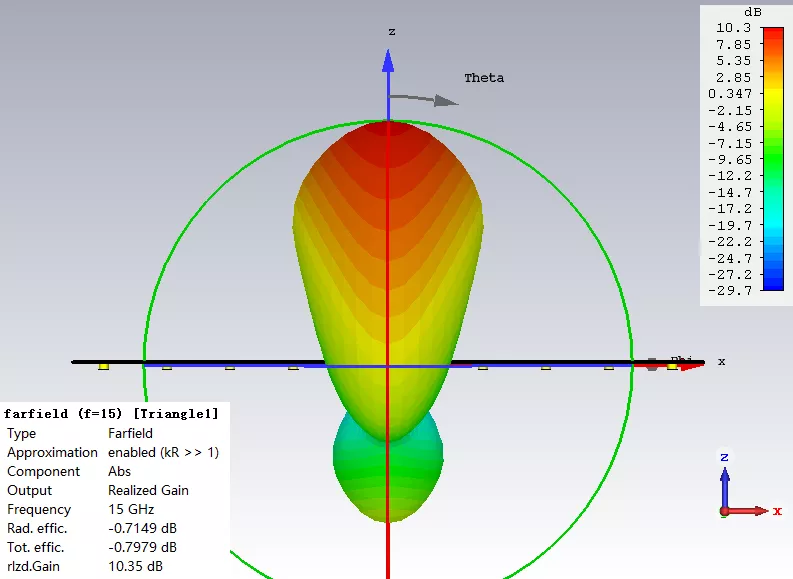
从上面的仿真结果可以看出，3dB波束宽度达到了30度，2D图像个子弹头。

从下图直观对比三组方向图可以看出，波束宽度越宽，其增益就会降低，这也符合理论经验。

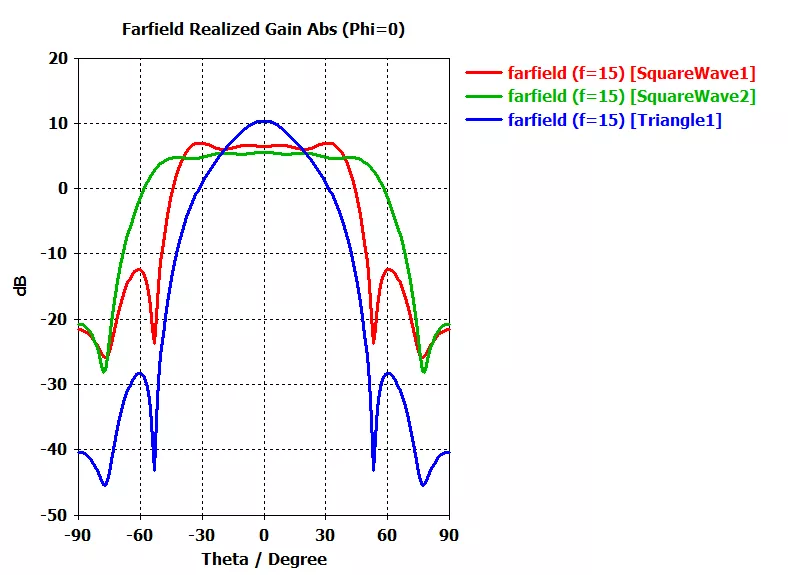
伍德沃德—劳森抽样法简单、优雅。然而，缺乏对旁瓣电平的局部控制能力也成为了其固有的缺陷。看到这里，有没有想用GA，PSO等算法优化激励幅度和相位的小伙伴？有兴趣可以一试。

END

本文为MWRF.NET原创文章，未经允许不得转载，如需转载请联系market#mwrf.net(#换成@)