技术

阵列天线的赋形波束综合(一)

2022-01-12 来源：微波射频网作者：94巨蟹座少年字号：大中小

学个Antenna是以天线仿真和调试为主，理论原理为辅的干货天线技术专栏，包括天线入门知识以及各类天线的原理简介、仿真软件建模、设计、调试过程及思路。如有想看到的内容或技术问题，可以在文尾写下留言。

摘要：

阵列天线综合问题是阵列天线设计的核心问题，综合方法很多并且发展迅速。最常见的有道尔夫-切比雪夫综合法，泰勒综合法，傅里叶综合法，伍德沃德法等。除了特定方向笔状波束的综合外，有时候我们需要实现方向图特定形状的赋形，比如余割平方波束等。

本文使用的软件为CST 2018和MATLAB 2019A

波束综合概论

在阵列天线处于接收状态时，进入其中的辐射能量来自于两部分：一部分能量从天线的主波束方向进来，即希望探测到的信号能量；另一部分则来自于天线的旁瓣方向。从主波束以外方向进来的干扰信号过大时，对于目标的探测和识别便会出现差错。为此，人们提出了低截获概率和低副瓣两种有效措施。在上次推文低副瓣阵列的设计原理中，我们也介绍了道尔顿-切比雪夫法实现阵列天线的低副瓣，并辅以一个10元线阵的实例进行仿真验证。

除了特定方向笔状波束的综合外，有时候我们需要实现方向图特定形状的赋形。比如需求视角内宽波束(方向图长得类似“方波”)，余割平方波束等。在浅谈阵列天线及布阵中，对于均匀直线阵来说，如果单元的激励电流幅度一致，相位递加/减，则其归一化阵因子如下图所示：

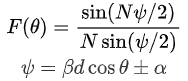
但是要实现特定形状的方向图，则需要优化出各个单元的幅度和相位。最暴力的方法当然是用算法进行全空间搜索，例如将每个单元的幅度和相位作为待优化变量，设计好适应度函数，用遗传算法不断进行交叉、重组、变异操作，使得当前方向图不断逼近目标值。除此之外，Fourier法和Woodward法也可以从理论上综合任意形状的方向图。
傅里叶级数法

在Phased Array Antenna Handbook和Antenna Theory: Analysis and Design书中，都对阵列天线的傅里叶级数法简单地理论阐述了一番。

这里简单复述下后者阐述的原理，对于一个N单元的线阵，若以整个阵列的中心作为参考点，则阵因子方向图可以改写为(左右滑动查看完整公式)：

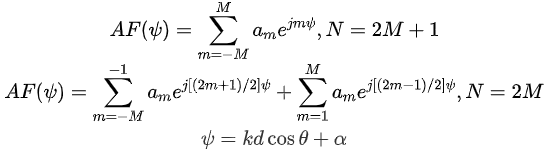
以奇数单元数的线阵举例，若等式左边如果是目标阵因子方向图，右侧则可看为一系列基函数。这就意味着可以参考傅里叶级数展开原理，得出综合目标方向图对应的各单元激励系数值：

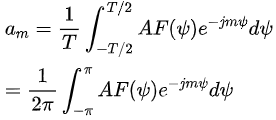
不过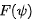展开为有限的傅里叶级数和，因此需在的可视范围内展开。若各激励单元之间同相，则。

假设有一个21单元线阵，其单元间距为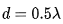，若归一化的目标阵因子方向图为：

将目标方向图和已知条件带入前面的公式，可得满足条件的每个单元的激励系数表达式为：

借助matlab软件简单计算后可得：

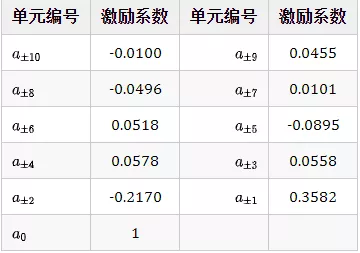
将该激励系数代入方向图综合公式进行反演计算，由于目标方向图在边缘区域中包含不连续性或者其值变化速度非常快，其反演方向图表现出震荡现象，这被称为吉布斯现象。

·吉布斯现象（又叫吉布斯效应）：将具有不连续点的周期函数（如矩形脉冲)进行傅立叶级数展开后，选取有限项进行合成。当选取的项数越多，在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时，该峰起值趋于一个常数，大约等于总跳变值的9%。

CST实例

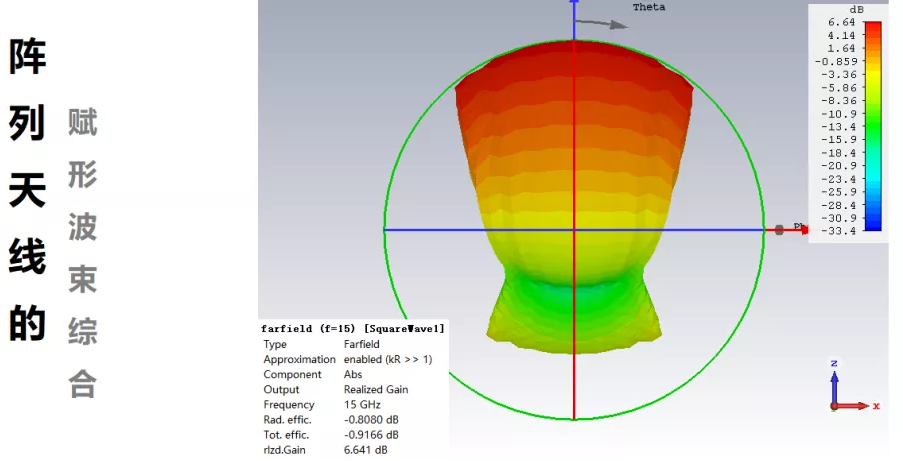
将浅谈阵列天线及布阵的模型略微修改下，使其工作频率在15GHz附近，工作频率半波长为10mm，间隔半波长布置21个单元。

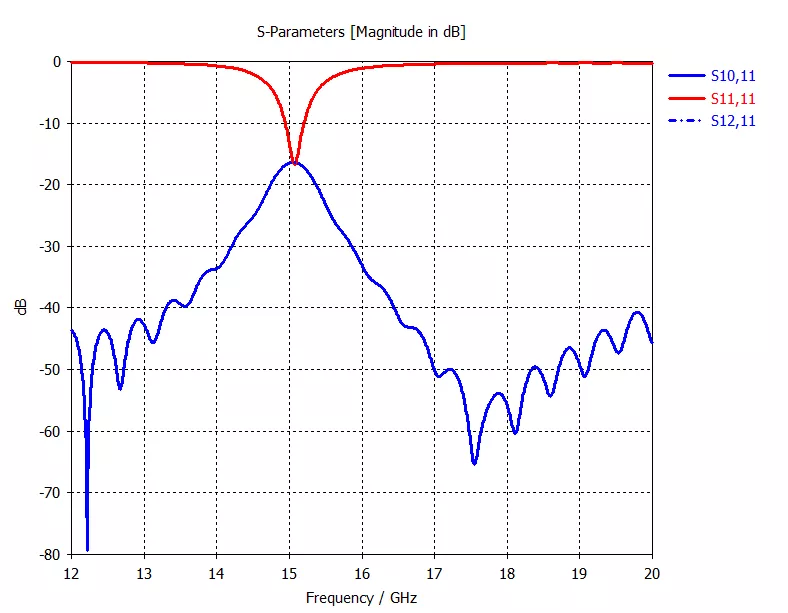
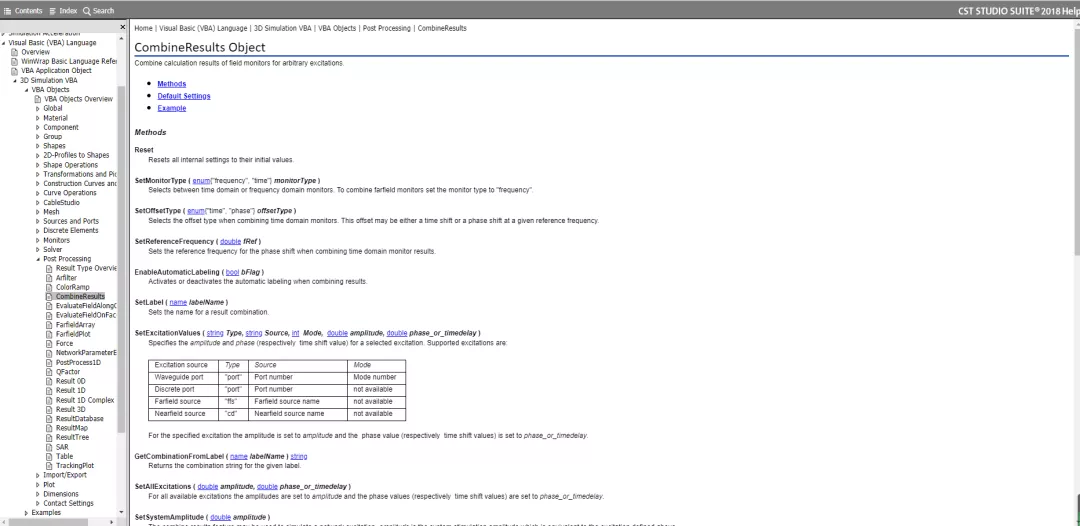
在CST的CombineResults里将前面计算好的单元激励系数设置进去，可以计算出一个方波似的方向图。如果手动输入一个个激励系数觉得麻烦，可以在CST界面里按F1弹出Help文档，这里面有详细的VBA脚本使用教程。

%Macro脚本参考文件

%可根据个人需求进行二次开发。

Default Settings

SetMonitorType ("frequency")

SetOffsetType ("time")

SetReferenceFrequency (0.0)

EnableAutomaticLabeling (True)

ClearFilters

AddFilter ("*")

SetNone

Example

With CombineResults

.Reset

.SetMonitorType ("frequency")

.EnableAutomaticLabeling (False)

.SetLabel ("My result combination")

.SetNone

.SetExcitationValues ("port", "1", 1, "Sqr(2.0)", 90.0)

.SetExcitationValues ("port", "2", 1, "Sqr(2.0)", -90.0)

.Run

End With

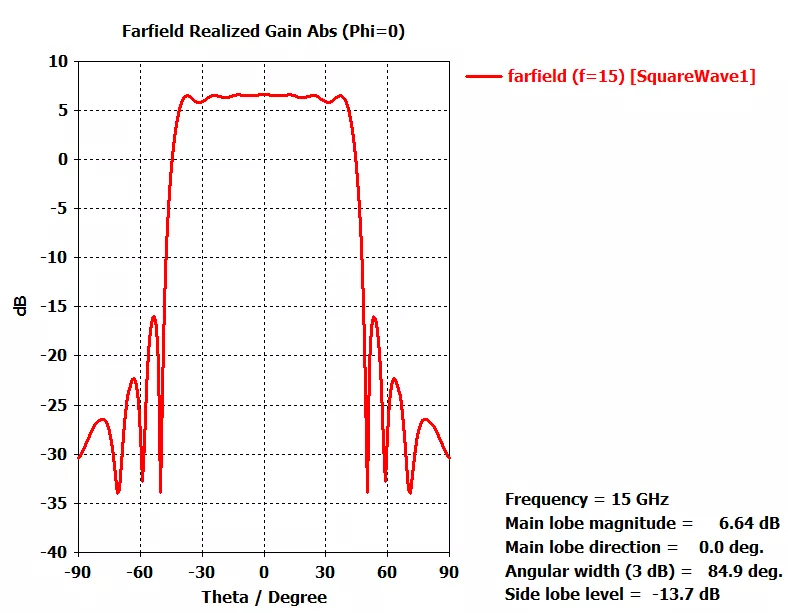
因为前面计算的阵列沿着轴排布，而上面的阵列是沿着轴组阵，因此看方向图时，加个就可，或者直接将下图的横坐标看成0~180°范围亦可。实际综合的方向图在±45°附近其实是快速衰减的，而中间部分的增益十分平坦。不过也可以发现实际综合的方向图是在理论的阵因子基础上乘以单元方向图，因为单元方向图并非全向，需要考虑到3dB波束宽度，因此相对于目标方向图，其波束宽度要略窄。

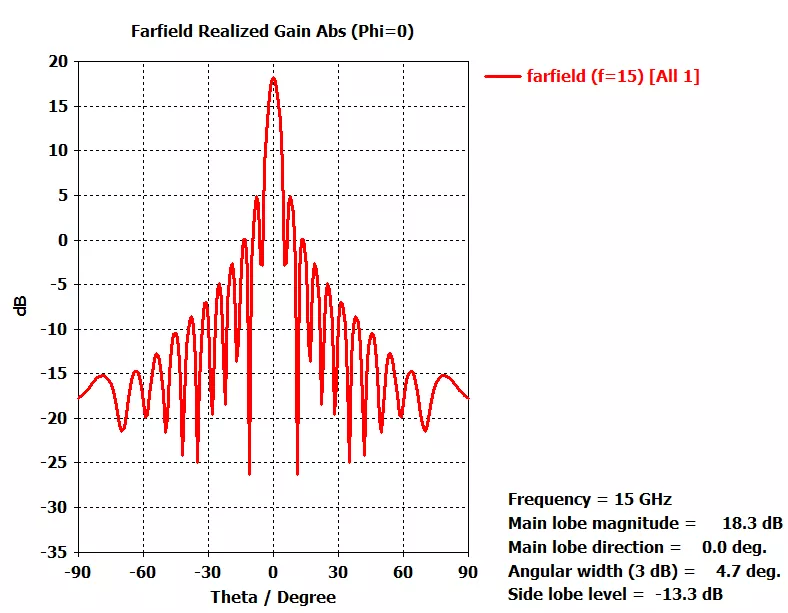
下面是单元等幅度等相位激励时阵列方向图，可以看出增益达到了18.3dBi，但是波束宽度仅有4.7°。有人肯定疑惑为啥放着高增益不要，去做波束赋形，这增益不是降低了么？其实这是根据实际需要产生的。例如在雷达探测时，用低增益宽波束去探测一个区域是否有需求目标只需要扫一次，然后再用高增益波束逐渐去进行高精度测角定位。两者在实际应用中相辅相成。