分形理论在天线技术中的应用

1  引言

随着无线通信技术的发展和移动通信终端设备的普及，特别是近年来人们对小型化、多频带、集成化天线的迫切需求，使天线技术得到了充分的发展。但是，传统的天线在几何形状上基本上都是基于欧几里德几何的设计。虽然，随着天线技术的不断发展出现了微带天线，具有低剖面、重量轻、成本低，可与各种载体共形，适合印刷电路板技术批量生产、易于实现圆极化、双极化、双频段工作等优点，但其致命的缺点是窄带性，从而限制了它的广泛应用。因此，迫切需要运用新的理论和方法，探索现代天线的设计，解决传统的天线设计中出现的问题和矛盾。研究发现，将分形几何应用到天线工程中，可设计出尺寸和频带指标更好的分形天线。

2  分形天线

“分形”这一概念是由法国数学家B.Mandelbrot 于1975年首次提出的,“分形（Fracta1）”这个名词即拉丁文的“破碎”。分形几何就是研究无限复杂而具有特定意义下的自相似图形和结构的几何学，自相似就是局部的形态与整体形态的相似，分形具有两大特征：自相似性和空间填充性(即分数维)。

所谓分形天线，是指几何属性上具有分形特征的天线。世界上第一个分形天线是由美国科学家Dr．Nathan Cohen 于1988年完成的，而对分形天线进行系统的研究是从1995年8月Cohen 发表他的第一篇有关分形天线方面的文章开始的。随后，国际上很多大学和科研机构开始对分形天线进行研究。分形天线是分形电动力学的众多应用之一。天线与阵列的分形设计是电磁理论与分形几何学的融合，如我们熟悉的螺旋天线和对数周期天线等一类频率无关天线都是分形天线，它已经存在多年，但直到分形技术应用后，它的性能才得以充分的理解。

传统的微带天线要实现其双频和多频工作通常需要采用多个辐射单元的天线或电抗性负载贴片天线或多频介质谐振天线，这些都增加了天线的复杂性，同时，也增加了制作的难度和成本。现代无线通信要求用低剖面、小尺寸、多频带（宽频带）、可集成的天线，分形天线能更好的满足这种要求。分形是通过迭代产生的分数维自相似结构，其整体与局部、局部与局部之间都具有自相似性。因此，分形是一种与标度无关的几何，与宽带天线的频率无关性比较相似。将分形应用于天线的设计主要是用来实现天线小型化和天线的多频特性，分形天线解决了传统天线的两个局限性：(1) 通常天线的性能都依赖于天线的电尺寸。这就意味着对于固定的天线尺寸，主要天线参数（增益、输入阻抗、方向图和副瓣电平等）将随着工作频率的改变而改变。分形的自相似性使分形天线有多频和宽频特性。(2) 分形的空间填充性，使一些天线的尺寸得到减缩。

分形天线的研究和应用，在军事和民用方面都有着巨大的潜力，尤其在无线、卫星和移动通信系统中将会发挥巨大的作用，有着非常广阔的市场前景。国外在分形天线单元和分形天线阵列研究方面已取得实质性进展，但国内在这方面的研究还很少，分形天线是分形理论和天线技术的融合，表现出与传统天线相比的许多优势，是近几年天线领域的研究热点。

2.1几种常见的分形天线

分形几何天线的形成主要是通过迭代的方式产生的，这就使得分形天线具有自相似性。如正三角形四等分成四个小三角形，挖去中间的一个，把剩下的三个小三角形四等分挖去中间的一个，如此无限的进行下去，面积将趋于零、边长增加、由无穷多线段组成的Sierpinski Gasket，如图2所示，其分维数为ln3/ln2。

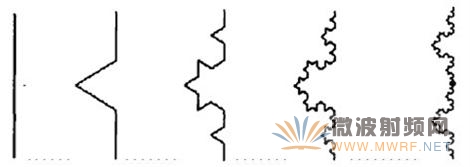
（a）Koch天线形成过程              （b）Koch双极天线
图1   Koch 分形天线

图2   Sierpinski Gasket分形天线的形成

图3   Koch雪花分形天线

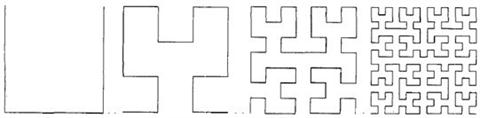
图4   Hilbert曲线分形天线

图5   Koch分形环和Minkowski分形环
图6   Sierpinski Gasket/Carpet 分形天线

2.2分形天线的特性分析

由于分形几何两个独特的特征：自相似性（self-similarity）（或自仿射性self-affinity）和空间填充性（space-filling），结合天线的特征，使得分形几何在天线工程领域中的应用有了突破性的发展。使天线在尺寸大小和频带宽窄以及多频带等方面的性能与传统天线相比有了极大的改善。

宽频带天线的重要特征是其性能与频率无关，如我们熟悉的螺旋天线和对数周期天线等一类非频变天线（即频率无关天线）都是分形天线。当频率变化时能保持其阻抗和方向图特性不变，即以频率为尺度时，其电性能不变。分形几何是一种与标度无关的几何，具有相似的结构，这意味着分形天线形状在不同的尺度变化下保持相似性，从而具有相似的电特性，形成多频带天线，从这一点上分析，研究分形几何与天线的关系有其必要性。

文献[1]中设计的Sierpinski地毯分形微带天线如图7，仿真和计算结果都表明，Sierpinski地毯分形微带天线具有多频带性，且最宽的频带达到中心频率的47.1％。文献[2]Sierpinski垫片分形天线也具有多频带性，这也证明了分形天线的多频带特性。实际上，不仅Sierpinski分形天线及其变形[3]分形天线表现出多频带性，而且分形树天线、随机分形天线也具备同样的特性。例如，利用等效RLC电路模拟法研究Dendrite类型的印刷分形天线[4]发现，Dendrite类型的随机分形天线在0.4-15GHz频率范围内也具备较好的宽带性能。

我们知道，经典的欧几里德几何研究的对象是规则而光滑的几何形状，而分形结构是由迭代产生的复杂形状，使一些天线的尺寸缩减成为可能。当然，分形严格来说，它是通过无限次的迭代而产生的复杂的几何图形，在天线的应用中我们一般只进行有限次的迭代，这并不影响天线的性能。与传统的天线相比，它更有效的占据空间，也就是分形天线的空间填充性，使得它在很小的空间内能有效的耦合从馈电传输线到自由空间的能量。通过分形环和分形双极子天线与线性环和双极子天线的比较得出：分形天线的空间填充性使得天线的尺寸缩小。实验也证明了这点：Koch曲线分形单极子天线如图1、Koch雪花如图3、Minkowski分形环天线如图5，它们的谐振频率都随着迭代次数的增加而降低[5]。这里，将着重讨论Koch曲线的分形天线的尺寸缩减性能。文献[6][7]重点讨论了Koch曲线的单极天线特性，它的分维数为㏑4/㏑3，当保持天线的高度不变时，见图1(a)所示，随着迭代次数的增加，曲线的长度将按4/3的倍数增加，天线的辐射阻抗增加，谐振频率减小，并趋于某一极限值，同时品质因数Q值减小，也趋于某一有限值。当利用两个Koch 曲线作为天线的两个振子时，即形成了Koch 双极子曲线。如图1(b)所示，Koch双极曲线的长度也随着迭代次数的增加而增加，辐射阻抗相应的增加，谐振频率逐渐减小，并趋于某一极限值。当保持双极曲线的谐振频率不变时，Koch曲线的长度在增加而高度在减小，见表1和图7，从表中我们发现，随着迭代次数的增加，天线的高度逐渐减小而趋向于某一有限值，而长度却无限增长。所以这种设计有利于天线的小型化,当然随着迭代次数的增加，也就相应的增加了天线设计的复杂度，因此，曲线的迭代次数不宜过大。

表1  Koch分形双极天线的高度与长度随迭代次数增加的变化

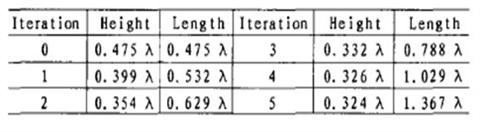
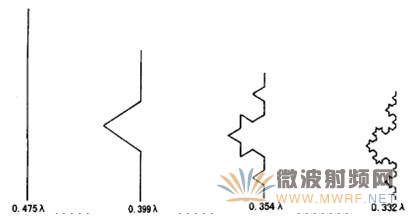
图7  Koch分形双极天线的高度与长度随迭代次数增加的变化(这里只画了一半)

具有尺寸缩减性能的分形天线还有分形贴片天线[8]。Hilbert分形天线，它的生成过程如图4所示，文献[9]对Minkowski分形环天线进行了深入的分析，表明Minkowski分形天线具有尺寸缩减性，同时随着分形迭代次数的增加，天线的尺寸缩减效应将趋于一极限值等。

3 分形理论在天线设计中的应用

分形天线的自相似性能减小分形天线元的整体宽度，同时和欧几里德几何天线元保持同样的性能，因为各个天线元具有同样的谐振频率和相同的辐射方向图。分形元能够改善运用欧氏几何天线元的线性天线阵列的设计，运用分形元来改善和提高天线阵列的性能，这里讨论两种方法：

一种方法就是减小天线元之间的相互耦合。因为线性阵列中天线元之间的相互耦合导致整个天线的辐射方向图性能下降。相互耦合还能改变天线元的激发电流。因此，如果在阵列天线的设计过程中忽略天线元之间的内部耦合作用，那么天线的辐射方向图就会受到影响，通常表现为副瓣电平的提高甚至导致零信号的填充。

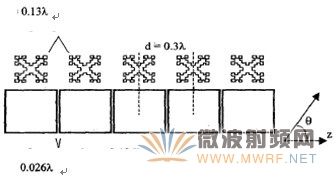
图8  中心距离相等的两种线性阵列

为了比较分形单元和传统的天线单元之间的相互耦合作用，阵列设计如图8 所示，两个阵列都有五个单元组成，单元之间的距离为d=0.3π，阵列单元的相位依次增加1.632弧度，主波束沿轴向扫描为135°。阵列的远场方向图如图9，从图中可以看出，两个阵列主波束扫描角度达到理想的135°，分形天线元阵列在45°方向上有较小的副瓣，同样，通过比较理想阵列元（不考虑阵列元之间的互耦作用）和分形阵列元之间的远场方向图，可以看出阵列元之间的相互耦合作用影响阵列天线的性能和零讯号的填充。在45°方向上，分形阵列的副瓣辐值比传统天线阵列的副瓣辐值小20dB，这意味着更多的能量加在主瓣上。

图9   阵列的方向图比较（ƒ（Ø）单位：dB）

另一种方法是在线性阵列中排列更多的分形天线元。这两种方法极大的扩大了线性阵列的有效扫描角度。分形也可以用来在一个线性阵列中放置更多的天线元，即一固定宽度的阵列天线，如果用分形天线元来代替，可以增加天线元的个数，同时减小了天线元之间的距离，这就使得阵列可以扫描到更低的角度，不会产生不期望的副瓣，这是因为在同样的谐振频率且保持天线元的边边距离不变的条件下，分形元尺寸较小，如图10所示，在中心距为0.5π的五个矩形环形单元线阵所占的空间中，排了七个分形环单元，且每两个单元的中心距为0.35π，矩形环单元相位依次增加2.72弧度，分形环单元相位依次：

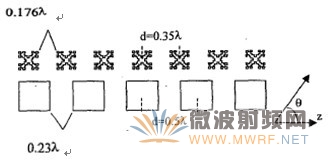
图10   相同宽度的两种阵列元排列

增加1.9弧度，都能实现主波束扫描135°。阵列的远场方向图如图11，从图中可以看出，在45°方向上分形元阵列的副瓣辐值比矩形元阵列低15dB。

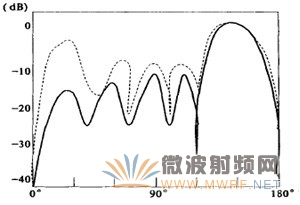
图11  两种阵列的方向图的比较

随着天线技术的不断发展，分形几何在天线中的应用也会越来越多,文献[10][11]分别研究了分形在MIMO天线和UWB射频设计中所获得的理想效果。我们知道微带天线有低剖面、重量轻、易集成，易于载体共形等特点，但是，这种天线的频带窄和难于实现多频带等固有的缺点限制了它的应用，如能把微带天线的辐射元用分形元来替代[8]，结合分形天线的特性，那将会极大的改善天线的性能。这必将是天线的一个发展趋势。这里，我们主要讨论了规则分形图形在天线领域的应用。随机分形天线分析也有文献探讨：随机分形图形更接近于复杂的自然形态的结构，这也是分形理论在天线设计中的一个发展。

4  总结

分形几何的两大特性应用到天线的设计中，解决了传统天线设计中的天线尺寸和多频带两大问题，同时，将分形运用到阵列天线的设计可以大大的改善和提高天线的性能。纵观分形天线的研究现状，分形天线的研究还处在初级阶段，还正待深入研究分形特性与天线特性以及天线性能之间的内在联系，促进天线小型化和多频带的发展。

参考文献

[1]  M.K.Rahim, N.Abdullah, and M.Z.A.Abdul Aziz. Microstrip Sierpinski Carpet Antenna Design. IEEE, 2005: p58-61
[2]  Yiftah Gelman, Ehud BerrAri and ReuvenShavit. Multiband Bow-tie Antenna Based on Fractal Geometry. 0-7803-8302-8/04/$20.00200 04: IEEE, pp3441-3444
[3]  Douglas H. Werner, and Suman Ganguly. An Overview of Fractal AntennaEngineering Research. IEEE Anlennasand Propagation Magazine. Vol.45, NO. I, February 2003
[4]  Jose Luis Sanchez, Leaandro de Haro. Experiences on Multiband Fractal Antennas. IEEE, 2001:
[5]  许峰. 若干分形天线分析研究. 西安电子科技大学硕士学位论文. 2002: 1-2
[6]  C．Puente，J．Romeu，R．Pou s，J．Rami S，and A．Hijazo. Small But long koch fractal monopole. Electtonics Letters 1998, 34(1): 9-10
[7]  C．Puente，J．Romeu，R．Pous，A．Ca rdama. The koch monopole : A sma11 fractal antenna. IEEE transactions on antennas and propagation. 2 00O: 48(11).
[8]  John P. Gianviffwb. and Yahya RahmatSamii. Fractal Antennas: A Novel Antenna Miniaturization Technique and Applications. IEEE,Antenna’s and Propagation Magazine.  Vol.44, No. 1, February 2002
[9]  王丽萍，许 峰，傅德民，龚书喜. Minkowski分形天线分析. 西安电子科技大学学报(自然科学版). V (29):
[10] 屠振，王理，王彪. 分形天线的特性分析及其在MIMO天线中的应用. 电子工程师. V(30)11:
[11] 孙华明，周正. UWB信号射频特性分析及分形天线的应用. Radio Engineering. 2004, V(34)9:

作者：钱四林,黄华,施建超