Nature Physics长文报道马仁敏课题组与合作者发现波与物质相互作用新形式

当我们按住琴弦的一端改变琴弦的长度，拨动琴弦，琴弦可以发出不同音调的声音，这是因为琴声是由琴弦的拨动和琴弦的长度等共同决定的。在物理学中，这一原理不光适用于声学，对光学和电磁学等学科也具有同样的指导意义。概括的来讲，辐射场（光场、声场等）并非完全是由辐射源本身的固有属性决定的，其所处的环境也起到了同样重要的作用。对这一波与物质相互作用基本观念的深入理解促进了量子力学与声学等学科的发展。

近日，北京大学纳光电子前沿科学中心、人工微结构和介观物理国家重点实验室马仁敏课题组与香港理工大学祝捷课题组、纽约城市大学葛力课题组等合作，理论预言并实验证实了突破波与物质相互作用基本观念的新形式，在电磁波和声波体系弹奏出“弦外之音”：辐射源可以激发出与其辐射环境无关的辐射场。相关工作被Nature Physics杂志以“Revealing the missing dimension at an exceptional point”为标题进行了长文报道。

以光与物质相互作用为例。在发光过程中，一直以来研究者都认为光源只能够与其所处环境的电磁场模式的本征态相互作用，光源的出射强度和频率等辐射特征由光源和这些本征态共同决定。这一观念随着对自发辐射的深入理解而逐渐形成。标志性的认识包括1930年V. Weisskopf and E. Wigner提出自发辐射是激发的电子与真空场相互作用引起的。1946年E. M. Purcell进一步指出自发辐射的速率是由光源和其所处环境的电磁场模式的本征态共同决定。对这一观念的深刻理解使得我们可以通过构建和调控光学模式本征态来控制光与物质相互作用，从而对激光器、单光子源、光子晶体、超构材料等光物理与器件的兴起与发展起到了举足轻重的作用。2012年的诺贝尔物理学奖正是授予了在此基础上发展起来的对单个粒子的量子调控。

图1、（a）普通环形谐振腔在一共振频率下有两个正交的本征态，处于共振频率的光源与其相互作用会同时激发出这两个本征态。（b）处于奇异点，共振频率上只存在一个逆时针传播本征态的环形谐振腔。处于共振频率的光源与其相互作用激发出了体系中不存在的顺时针传播的本征态。（c）环形谐振腔中本征态随着时间-宇称对称折射率调制的演化。在奇异点处两个本征态是完全平行的。

为了探究光与物质相互作用新形式，团队对非厄密系统中的奇异点（exceptional point）进行了深入的探索。在奇异点，系统不只是本征能量简并，而且本征矢量合并在了一起。此时本征矢量形成的希尔伯特空间为不完备的（图1）。以一个环形谐振腔为例，在其一个共振频率上存在两个正交的本征矢量，分别对应顺时针和逆时针传播的本征态。通过引入宇称-时间对称折射率调制之后，可以构建出共振频率上只存在一个逆时针传播的本征态的奇异点。团队在这一光学奇异点引入单个偶极子辐射源，发现这个辐射源可以完全不激发体系唯一存在的逆时针传播的本征态，而是激发出了体系中不存在的顺时针传播的本征态。在数学中，奇异点处缺失的态矢量被称为约当（Jordan）矢量。这一现象是首次在物理体系中观测到约当矢量被直接激发出来。同时，由于激发出来的约当矢量具有轨道角动量，基于这个现象可以将单个辐射源的辐射场转变为带有轨道角动量的涡旋波束（图2）。因此，该发现不仅改变了光与物质相互作用基本观念，丰富了奇异点的物理，同时也可被用来产生和调控新型光场或声场。

图2、（a）偶极子辐射源在普通电磁环形谐振腔中激发出的辐射场。（b）引入宇称-时间对称折射率调制之后处于奇异点的环形谐振腔的辐射场。（c）偶极子辐射源激发的处于奇异点的环形谐振腔的辐射场。

这一物理现象在波与物质相互作用中具有普适性，不仅在电磁波体系中存在，而且在机械波系统中也存在。团队在宇称-时间对称折射率调制的声学腔中也观测到了此现象（图3）。图3a中腔体内壁的声学人工结构能够在复平面上调节等效折射率，使其满足宇称-时间对称并工作在奇异点附近。此时腔体内的本征态是非厄密简并的逆时针模式。而当一个单极子声学点源被放入腔体内的特定位置时，激发的顺时针单向声场呈现出与本征态完全相反的手性。这一独特现象暗示了声学轨道角动量调控的一个额外自由度，为声学通信和粒子操控带来了全新的可能。另外，声波不具有自旋属性，而团队所展示的这种手性声场则可以充当声学系统中的赝自旋，服务于拓扑声学的研究。

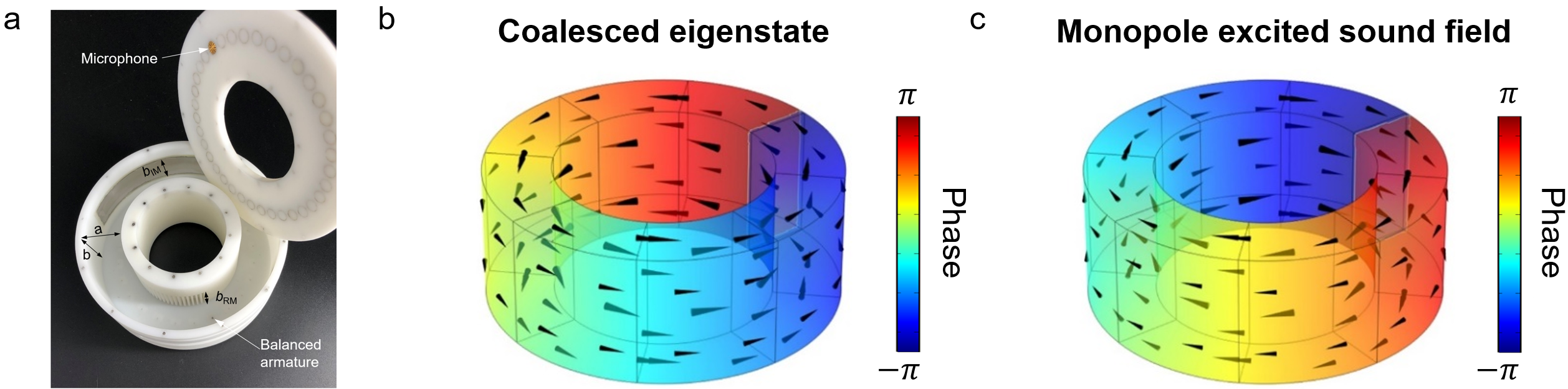
图3、（a）具有宇称-时间对称折射率分布的声学环形谐振腔样品。（b）和（c）奇异点处的腔体内部声场的相位及声能流方向。（b）为本征态，（c）为单极子激发声场。黑色箭头代表声能流方向。

在该工作中，马仁敏课题组通过理论分析和数值模拟发现了这一现象并在电磁波体系进行了实验验证，祝捷课题组在声波体系进行了实验验证，葛力课题组进行了格林函数约当矢量分析。北京大学陈华洲、香港理工大学刘拓以及北京大学栾弘义为共同第一作者；马仁敏、祝捷、葛力为论文通讯作者。论文作者还包括中科院物理所陆凌、北京化工大学王兴远、华中科技大学祝雪丰以及英国伯明翰大学张霜等。工作得到了国家自然科学基金委、科技部、北京市自然科学基金、纳光电子前沿科学中心、人工微结构和介观物理国家重点实验室、量子物质科学协同创新中心等的支持。