高频应用中使用LTCC技术的3-D超材料的制造

I．介绍

在1952年，Schelkunoff和Friis[1]提出由于人工介质的磁导率持续增长，应该使用开环谐振器（SRR）。尽管他们提出了磁导率方程，但是在讨论介电常数和磁导率的结果被否决后，他们没有这么做。在1968年，Veselago[2]提出在不违反麦克斯韦方程和坡印廷定理的情况下，材料可能具有小于1甚至是负的介电常数和磁导率。看来，这个文件被忽视了近30年，直到Shelby，Smith和Schultz[3]通过制造一个有拆分环和细线结构的样品，这个样品在微波的频率下的楔形容器内展示出了负折射，从而实验式地验证了Veselago的假说。Pendry和同事们[4]的开创性论文给了他们的实验工作很多的援助[5]。在他们的第一篇论文中，Pendry等人描述了在有效媒介的介电常数低于等离子体频率的情况下，周期性分布非常薄（小于0.01 λ）的电线是如何能引起类似血浆的行为，这取决于电线的宽度和间距以及介质嵌入的位置。在他们的第二篇论文中，他们描述了如何电动小分裂环的周期分布（约为0.1λ）可以产生一个有效的媒介，具有高度色散磁导率，在等效LC电路的共振频率下可以成为负的。超材料的名称被用来形容不寻常的这些材料的频率响应，前缀“meta”在希腊字中，意思是“超越”[6]。在过去10年中，在超材料领域的研究已发生爆炸，数以百计的论文已经发表，其中大部分的理论提出超材料使用于各种微波和光学应用[7]–[12]。

我们用Schelkunoff和Friis使用过的方法，来获得用RLC等效电路模型收集的小SRR的磁导率。如果入射磁场是垂直的SRR平面，感应电流的流经循环可以用下公式表示：
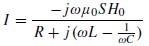（1）
其中ω为频率，S是环路面积，Ho 为磁场的振幅，L是等效电感的SRR和C是电容的SRR的间隙，C是SRR间隙的电容。如果SRR是小电气性的，则等效磁偶极矩的SRR可写为Pm =IS。这类SRR集合的磁化强度（每单位体积的磁偶极矩）可以写作：
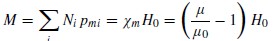（2）
其中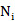 是第i个类型单位的SRR数量，Xm 是磁化率，μ是超材料的有效磁导率。通过带入（1）中感应电流的表达式，我们可以写出SRR的电感L、电容C和电阻R的有效磁导率。如下：
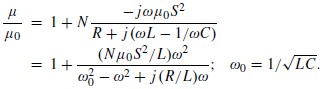（3）
我们观察到，当该场的频率与电路的共振频率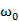 =1/LC一致，我们可以得到一个大的磁导率值。因此磁超材料的透气性，完全由于共振影响。远离共振区域，超材料是无磁性的。等效电感L和电容C可以用不用的SRR几何模型来算出。我们看到，这个简单的推导，可以用感应电流的概念给出一个超材料的磁导率表达式，这与许多作者所用的Lorentz模型相同。通常被写作
（4）
我们把复介电常数和磁导率各自定义为ε' ±jε'' 和μ '''' '±jμ ''。物理学家更喜欢正号，而电气工程师更喜欢负号。绝大多数的自然材料 ε ＞0，μ ＞0。金属在光频段ε  ＜0，μ ＜0。抗磁材料ε  ＞0，μ ＜1。所有的超材料在共振频率，表现出高度分散行为。在共振频率，传输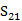（ ）始终是一个最小值，伴随着在附近频率下的反射最小值。根据共振的强度和性质，介电常数的实部、磁导率的实部，或者两者一起，都能是负的。用Nicholson–Ross–Weir方法提取的介电常数和磁导率保证了材料是无源的，即复阻抗的实部是正的，波数的虚部导致了波在介质中的衰减。我们避免说明虚部是正的或是负的，由于虚部的正号或负号复属性定义导致的可变性。当我们进一步得到介电常数的虚部和磁导率，超材料拥有的介电常数和磁导率有正值和负值。对于普通的介质材料，介电常数的虚部将满足条件的因果关系。这对于负介电常数和负磁导率来实现负折射率是不是必须的。

微波异向介质的实验表征，和平面超材料测量的S参数的提取出的复介电常数和磁导率是由Varadan和Tellakula完成的[13]。图1显示的SRR是一个电小差距的细线环。这种SRR结构可以导致电场和磁场的共振。当环轴与H场平行，SRR的H场产生电流，从而引起强大的磁偶极子，因此磁共振。如果SRR的间隙与E 场平行，E场在间隙中产生一个变化的电压，导致了一个强大的磁偶极子，这会引起电谐振。对于一对对称的SRR，磁共振受激，两个SRR的磁偶极子应该加起来，而电偶极矩相互抵消[14]。对于电谐振，两个电偶极子应该加起来，而磁偶极子抵消。

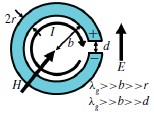
图1 拆分环谐振器

在以前的实验工作[3]，[13]-[19]，印刷电路板（PCB）技术和湿法刻蚀被用来沉积介质基片等金属的共振结构例如FR4及Duroid。这些样本可用于平面传输线样品，其中波的传播可以是在平面结构上或是垂直于平面结构。打个比方，这些在[3]和[13]中用的样品，不能被用于实际应用。在本文中，对于3-D互连的超材料制造的低温共烧陶瓷（LTCC），表现出的每种设计规范所表现出的超材料色散现象，我们提出了一种设计方法。LTCC工艺被广泛用于工业微波和电子电路的封装，多层电路技术，并用于方便嵌入无源器件，如电感，电容和电阻。它可以封装提供的3-D电气连接中间层，其中在所需的位置用金属填充微通孔，这种能力也是很有吸引力的。LTCC工艺特别适合制作高频系统启动的封装，用于天线阵列，单片微波集成电路（MMIC）等[21]-[24]。

LTCC工艺可以成功地用于3-D超材料的制造，并提供了很大的改善和很多的功能功能，相对于目前的用PCB平版印刷技术制造的2-D超材料方法。对于MMIC的应用，结合基板上无源但共振的超材料结构将有几个优点。超材料的LTCC基板可以用来控制电磁干扰，并为内部的高频元件和外部的干扰源提供隔离和条块分割。

据我们所知，这是第一次系统地应用LTCC工艺来设计，制造和表征/验证用于毫米波的超材料。在本文中，我们首先描述与LTCC制造步骤相匹配的3-D超材料制造的设计过程，以及将这个设计与2-D超材料相比较。然后，我们描述了这种使用Ansoft公司的高频结构仿真（HFSS）的商业代码的全波仿真的电磁建模结构。在数字化设计中，我们计算了一块LTCC超材料板的S参数期望，和在烧制工艺中的收缩率期望。对于一些样品，计算出的S参数被用来抽取超材料的介电常数和磁导率。这种设计后来使用自由空间测量系统而被制造和实验特征化[13]。

图2 杜邦951基板上的2-D SRR单元

将仿真和测量数据进行了比较，两者符合得非常好。我们也提出了一种常用LTCC基板的复介电常数，杜邦951生瓷带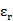（  =7.4−j0.026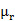， =1）的频率范围为5.8–110GHz。这个数据对于其他研究人员在其设计中使用杜邦951是非常有用的。

LTCC工艺对于超材料制作是一个非常容易和成本效益的方法。它是一个容易被封装行业所接受的工艺，现在也在快速增长的超材料领域中有很好的应用。

II. LTCC超材料的设计过程

A．2-D超材料

首先，我们设计了LTCC介质基板的2-D SRR。单元如图2。这种SRR是用银墨印刷在一种杜邦951 LTCC薄膜上。它有用全波仿真器仿真的各种规模。基于有限元全波麦克斯韦求解，用Ansoft HFSS进行仿真。仿真一个周期阵列SRR的反射和透射系数，周期性边界条件被用于单元的横向边界辐射边界条件的取得，通过用一个完美的匹配层边界条件来输入和输出平面波。

表I中，我们将在共振频率下的每个SRR的半波长与SRR平均周长进行比较。共振频率的频率有一个最低的传输系数（S21 ）。半波长和平均周长按下面的方程计算：
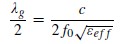（5）
平均周长= （6）
其中c=3× （mm/s）， 是SRR的共振频率。由于SRR放置在空气和LTCC基板之间，我们假设有效介电常数为4.2，这是空气和杜邦951（  =7.4）的平均介电常数。

表I共振频率半波长及SRR结构的平均周长

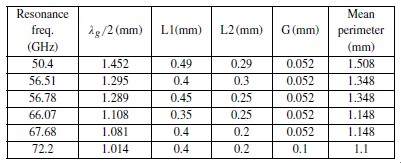
我们可以观察到在各种情况下，平均周长要比半波长稍大一些。在共振频率下，周长是半波长的整数倍时就会出现驻波。由于有效介电常数是近似值，所以有小的差异。空气中50GHz下波长为6mm，基板厚度小于0.1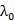 。薄基板能产生一个较低的有效介电常数。如果入射H场是垂直于2-D SRR轴，磁共振是不受激的[13]。

B．3-D超材料

3-D超材料是基于多层杜邦951 LTCC薄膜设计的，这可以使电谐振和磁共振都能发生。图3为概念的示意图。3-D SRR有一个由金属线和两个金属填充的微通孔组成的环。金属线是由金属填充的微通孔立体连接的。微通孔的半径为0.065毫米。允许收缩的相邻SRR间距为0.87毫米。图3展示了线宽尺寸、长度和间距。每条金属线有一条与入射E场平行的间隙。3-D SRR的轴与H场平行。因此，3-D SRR 能被E场和H场受激。不断仿真S参数直到我们得到了所需的共振频率和别的特征，这种设计在几次迭代后产生。

3-D SRR的平均周长为1.148mm（0.3mm×4-0.052mm）。因为SRR是完全嵌入在LTCC介质中的，用杜邦951（7.4）的电介质常数代替平均介电常数（4.2）来计算共振频率，计算出来的共振频率为48GHz。然而，SRR顶部和底部的金属线受空气影响，因此这个共振频率只是一个简单的粗略值，必须用全波仿真进行改善。预期的共振频率是近50GHz，这是高于计算得出的共振频率。我们需要有效地计算研究介电常数的研究。

III．3-D超材料的LTCC制造

设计好的3-D SRR是通过LTCC工艺制作的。首先应考虑绿膜的收缩。在共烧期间，绿膜收缩13%，因此SRR用于印刷的屏幕尺寸和通过填充的模板尺寸应该被放大。在烤箱中120 ℃下预处理30分钟空白陶瓷绿膜后，用机械冲压机打孔微通孔，并用杜邦6141银浆填充中间层，如图3（b）。在银浆中用模具保护生瓷带的其余部分。然后，用屏幕和杜邦6142D银墨将金属线印刷在底部上层和顶层的底部。在90 ℃的烘箱中干燥银墨5分钟后，每层在70 ℃和3500磅下层叠和层压10分钟。然后，LTCC在875 ℃下烘制15分钟。图4展示了共烧前层的照片。底层有SRR金属线，中间层有金属浆填充的通孔，金属线印刷在通孔上。图5中，制造的样品被切开，和仿真的SRR进行比较。测量了几个点的总厚度，样品的厚度为0.284±0.003毫米。厚度收缩率略高于预期。我们还可以观察到层对齐时，SRR的间隙移位。

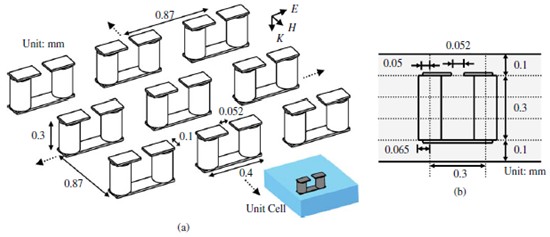
图3 （a）杜邦951电介质的3-D SRR（b）侧视图

图4 共烧前的每层照片。中间层有通孔和金属线。底层只有金属线。

图5 （a）仿真SRR的侧视图（b）共烧之后SRR制造的侧视图照片（单位：mm）

IV．用聚焦高斯光束的自由空间表征

LTCC 3-D SRR样品是用自由空间测量系统测定的[13]，[25]。图6展示的是一张照片和自由空间测量系统的示意图。两个有介质透镜的喇叭天线是用于发送和接收集中的高斯光束平面波。LTCC超材料样品被放置在两个天线之间，通过完整的双端口后，反映和线标定。向量网络分析仪精确测量大小，杜邦951样品（150mm×150mm）表面的反射相位和透射系数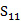（ 和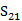 ），使用聚焦光束省去了原本需要的暗室。

使用尼科尔森罗斯威尔反演法[24]测量S参数，可以得到复介电常数和磁导率。图7给出了一个用于频率范围为5.8–110 GHz的空白杜邦951 LTCC基板（厚度=1.047毫米）的介电常数。在65GHz以下我们用1.8毫米连接电缆，在67到110 GHz之间用1毫米的电缆。因此，65到67GHz之间的数据是缺失的。在整个频率范围内，杜邦951的介电常数（ ε ' ）的非常稳定的（7.4±0.2）。

图8显示了图3中的3-D SRR样品的仿真和实测数据。测量结果与仿真结果非常符合。测量的共振频率（51.7GHz）比仿真略高（51 GHz），因为由于高于预期收缩，制作的几何模型小于仿真的几何模型。传输系数的测量幅度小于从48至53GHz的-10分贝。这是超材料的阻带，如果在MMIC中，可以被用来作为一个过滤器或屏蔽材料。

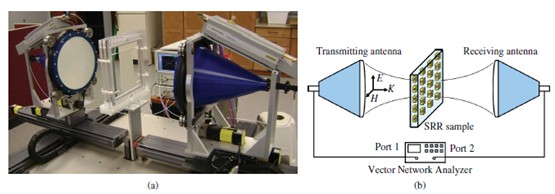
图6 （a）照片（b）自由空间测量系统的示意图

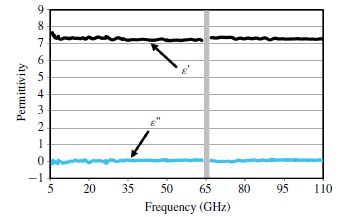
图7 空白杜邦951基板的测量介电常数

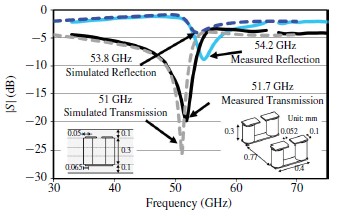
图8 仿真和实测的杜邦951电介质的3-D SRR反射和透射系数

V．对称双3-D SRR

我们修改了用于双共振的对称双SRR（ = ）的单元，如图9所示。相邻对之间允许收缩的空间仍是0.87毫米。图3显示的3-D SRR有电谐振和磁共振，因为间隙平行于入射E场，轴平行于H场。然而，磁共振是如此之小，我们可以看到只有一个电谐振。磁共振可以由一个强大的对称双SRR之间的电容耦合增加。因此，我们也可以得到双电磁共振[14]，[26]。

我们通过改变有通孔的中间层厚度，将两种样品，即三层和五层的样本，认为是两种样品。图9（b）和（c）为每个样品的侧视图。由于增加了SRR的大小，五层样品比三层样品有更低的共振频率。图10显示的是仿真反射的程度（ ），B波段、V波段和W波段（33–110 GHz）的传输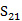（ ）系数。图10（a）展示的五层样品，我们观察到| 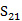|中45.2和56.6GHz下的两个独立的最小值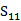，| |中43.8和60.8GHz下也有两最小值。图10（b）展示的三层样品，|S21 |的最小值在74.4和94.2GHz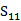，| |的最小值在73.6和102.8GHz。| 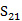|的最小值为SRR的共振。自从中间层厚度减少，SRR规模变小，三层样品的共振频率增加了30–40 GHz。

五层的样本在45.2 GHz的共振，是一个磁共振，因为S11 的最小值（43.8 GHz）是之前S21 的最小值（45.2 GHz）。这解释了之前[14]图11（a）和（b）展示的45.2 GHz下的SRR表面电荷分布和电流方向。在相邻SRR位置，H场激发了相同方向的电流和相反符号的电荷。因此，单元产生一个净磁偶极矩，没有净电偶极矩，导致了磁共振。符号相反的SRR的电荷产生了一个耦合电容。在56.6 GHz的共振是电谐振，因为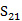 的最小值（56.6 GHz）是之前 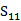的最小值（60.8 GHz）。图11（c）和（d）显示了E场在间隙中产生了电压变化，在相邻SRR位置电荷密度有相同的符号。我们观察到，有净电偶极矩但无净磁偶极矩，因为电流在相邻SRR方向相反。

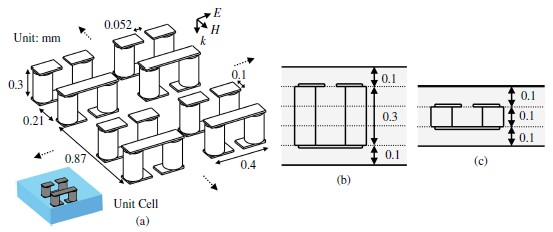
图9 （a）LTCC电介质上对称双3-D SRR周期点阵（b）五层样本的侧视图（c）三层样本的侧视图

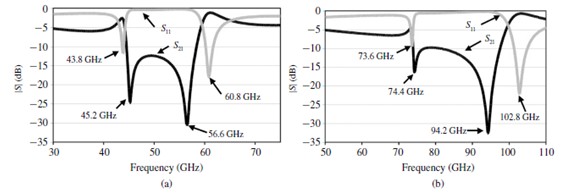
图10 （a）五层样品和（b）三层样品的仿真反射系数（ ）和传输系数（ ）

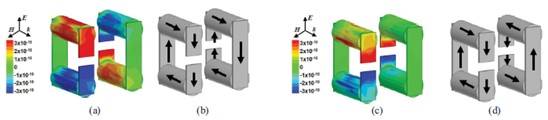
图11 （a）45.2GHz的表面电荷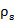（ ）（b）45.2GHz的表面电流分布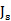（ ）（c）56.6GHz表面电荷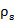（ ）（d）电流分布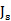（ ）（入射E场假定为1V/m）

VI．对称双3-D SRR的实验表征

用自由空间测量系统的对称样本还有一个特点。图12展示的是测得的空白的电介质和SRR介质的传输系数。65到67GHz之间的测量数据缺失，因为在这个波段不能使用1和1.88mm的电缆。图10展示了45.2和56.6GHz下五层样品耳朵仿真数据有双共振。然而，在略高于46.6和60.2频率下，测量数据有共振，这是由样品的收缩比预期高造成的。图5显示的是归因于对准误差产生的一些错误。我们在屏幕印刷和堆积层中用对准标记。准误差产生了超材料结构电长度的变化，自从结构被嵌入在陶瓷基板上，共烧后准误差的影响很难评估。此外，LTCC工艺中微观结构的收缩可能不平衡。频移的响应很大，因为在毫米波段其波长很小。五层样本中1.4GHz-3.6GHz的仿真数据和实测数据的共振频率有差别。

当LTCC介电常数用于封装，空白的介电常数没有阻带，波能通过整个波段的介质传播。然而，在45-62GHz波段中，入射波不能通过SRR的LTCC介质传播。图3中SRR的阻带增加了5到17GHz。对称对属性是由SRR的定位来改变的，即使规模和大小与图3中的SRR相同。频率范围和通带及阻带的带宽可以很容易地通过修改单元的结构设计。这对于允许理想信号进入包，防止不良信号渗入包的封装有不错的应用。

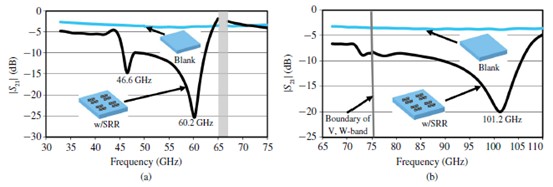
图12空白电介质和SRR电介质的实测传输系数（ ）比较（a）五层样品（b）三层样品

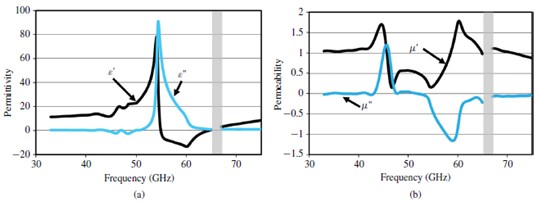
图13 五层样品实测数据计算出的有效（a）介电常数（b）磁导率

图12（b）展示了三层样本之间的比较。图10（b）中74.4和94.2GHz的仿真数据有共振，101.2GHz的实测数据有共振。我们无法观察到75GHz下实测数据的第一共振，因为它非常弱，而且接近V波段和W波段的临界。仿真数据和实测数据的第二共振频率差别在7GHz，这高于五层样本。这表明对准误差的影响可能与频率成正比。在90–105GHz波段的SRR中，入射波无法通过三层LTCC介质传播。

图13提出的五层样本的有效介电常数和磁导率是用尼科尔森罗斯威尔方法[13]，[25]测得传输和反射系数后计算得出的。介电常数和磁导率高度分散在共振频率附近。因为电谐振，60.2GHz下介电常数的实部是负的。因为磁共振，46.6GHz下磁导率的实部接近于0。

VII．总结

我们已经证明，LTCC技术可以成功用于2-D和3-D形式的毫米波超材料制造。我们设计的超材料结构与LTCC工艺兼容，使用多层陶瓷膜进行设计。采用自由空间测量系统测量SRR的共振。测量结果与仿真数据相符合，除了对准误差引起的频率位移以及略高于期望收缩。这可以由更准确的对准方法和不同类型的超材料微观结构收缩效应的系统化研究来改善。我们证明了材料的共振频率可以通过改变SRR的大小来调整。通过简单地引入一个LTCC材料的额外层，增加SRR三维高度的能力导致了成本的节约，因为不需要新的屏幕或者罩来实现其他的共振频率。

我们设想将LTCC工艺用于许多不用的应用，包括如天线超材料、天线罩超材料、MMIC的无源基板元件，如过滤器、移相器、减少高频EMI的封装材料，如减少天线阵列的视觉和雷达信号的基板和覆盖物。

感谢

我们非常感谢F.Barlow在开展低温共烧陶瓷工艺时的指导和帮助，那时他是费耶特维尔的阿肯色大学教师。

作者：Vasundara V. Varadan，IEEE高级会员和In Kwang Kim，IEEE会员