汽车毫米波雷达距离测量中的一种扩展卡尔曼滤波实现

本文详细描述了卡尔曼滤波器在汽车毫米波距离测量应用中的工作原理，详细介绍了卡尔曼的工作原理，实际测量中的噪声来源，并在搭建好模型后运用MATLAB分析验证了模型的有效性。

毫米波雷达对待测目标进行间隔时间为T的一系列测量，获得距离，速度和角度信息，这些测量信息中因为包含测量噪声，所以我们不能完全采信这些测量结果。同时，我们假设待测目标按照匀加速度模型进行运动，那么当前状态下的待测目标距离可以按照待测目标上一状态的距离，速度信息依据牛顿线性模型计算得出，但是这种牛顿线性理想模型未能考虑其他能破坏模型的外力作用，比如待测目标的动力输出不可能是恒定不变的，地面阻力以及风的阻力也不是恒定不变的，因此按照牛顿线性模型推算的结果是缺损的，未能考虑其他外力作用。卡尔曼滤波器可以很好的平衡含冗余噪声的测量结果和缺少信息的过于理想的计算结果，并实现对待测目标的准确跟踪。

1、卡尔曼滤波介绍

卡尔曼早期最成功的应用案例是在阿波罗登月计划中成功解决了轨道预测问题。由于卡尔曼滤波是一种时域滤波方法，其算法采用递归形式，便于在计算机上实现，目前，卡尔曼滤波被广泛应用在惯性制导，地图导航，雷达测量等各个领域。总结起来，卡尔曼能解决的问题特征为：一是不能对待测目标进行准确建模，外力作用不稳定，但是掌握外力作用效果的统计值；二是虽然可进行一系列的测量，但是测量结果因含有噪声而不能完全采信。

毫米波雷达测量示意图如图1所示，假设雷达的测量周期T，时刻nT的测量向量记为u(n),

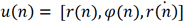    (1)

r(n)代表目标相对于雷达的径向距离，φ(n)代表目标相对于雷达角度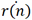，代表目标相对于雷达径向速度。由于毫米波雷达测量得到的距离速度等信息都是径向的，因此测量向量u(n)是在极坐标系下获得的。

图1、雷达目标测量示意图

但是为了便于利用简单的牛顿线性预测模型对目标进行跟踪，也即对待测目标连续两次时间间隔为T的两个状态进行关联，我们需要获得笛卡尔坐标系下待测目标的距离，速度等信息。由于测量是在极坐标系中而状态跟踪是在笛卡尔坐标系，因此需要进行坐标系转换。由于这种坐标系的转换是非线性的，因此需要使用扩展卡尔曼滤波器。      

假设笛卡尔坐标系下待测目标在时刻nT的状态向量记为S(n):

    (2)

其中x(n),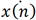,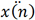分别代表nT时刻待测目标在x轴方向上的位置，速度和加速度。y(n),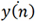,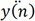分别代表nT时刻待测目标在y轴方向上的位置，速度和加速度。

卡尔曼滤波器算法是按照递归工作的，假设已知待测目标的状态向量S(n-1)，待测目标按照匀加速度进行运动。利用牛顿线性模型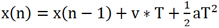得到的从状态S(n-1)到状态S(n)的转移矩阵定义为F：

    (3)

基于转移矩阵F和(n-1)T时刻待测目标的状态向量S(n-1)，我们可以得到nT时刻的待测目标的状态估计向量S_apr (n)如下：

S_apr (n)=F*S(n-1)    (4)

由于匀加速度模型过于理想，不符合待测目标的实际运行状态，也即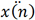和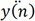无法保持恒定不变，因此S_apr (n)获得的距离信息是缺失的，未能考虑其他破坏匀加速度模型的外力作用，我们假设这些外力导致待测目标在x轴和y轴上加速度变化为w_x(n)和w_y(n)，那么考虑外力作用后的待测目标的状态向量S(n)如下：

    (5)

    (6)

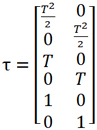    (7)

定义w(n)引入的状态变量变化的协方差矩阵Q(n)，其中w_x，w_y为省略下标n的简写，

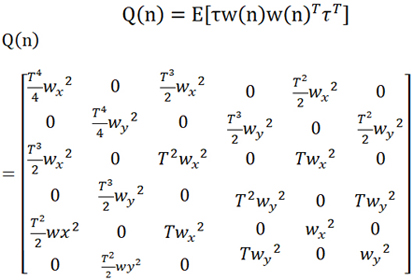    (8)

S_apr (n)中完全不含有τw(n-1)导致的状态变化，由于无法准确量化w(n-1)，也可以理解S(n)始终不能完全涵盖τw(n-1)，实际上S(n)中还未考虑状态向量S(n-1)中缺失的信息，我们定义S(n)中缺少的信息总和为d(n)，由于同样无法准确计算d(n)，我们期望通过递归收敛的方法解决d(n)。定义d(n)的协方差矩阵为P(n)=E[d(n) d(n)^T ]，P(n)矩阵大小为6*6。假设我们已知P(n-1)，那么可以推算出P_apr (n)，公式如下：

P_apr (n)=F*P(n-1)*F^T+Q(n-1)    (9)

F*P(n-1)* F^T可以理解为S(n-1)状态缺少的信息通过转移矩阵F到状态S(n)时产生的缺少信息的协方差矩阵，Q(n-1)为外力在时刻(n-1)T到时刻nT时间内引入的状态协方差矩阵。

测试向量u(n)和我们要求解的状态向量S(n)描述的是同一个待测目标，其关系式如下：

u(n)=H(S_apr (n) )+J_H (S_apr (n) )[S(n)-S_apr (n) ]+v(n)    (10)

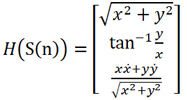    (11)

其中H(S_apr (n))表示将笛卡尔坐标系下的向量S_apr (n)转换到极坐标系中，在上述公式中，测量向量u(n)通过非线性关系与状态向量S(n)相关。因此，我们使用扩展卡尔曼滤波器，通过仅保留泰勒级数展开式中的第一项，简化了u(n)和S(n)之间的关系，偏导数矩阵J_H (S(n) )定义如下：

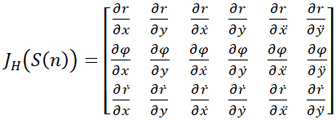    (12)

定义y(n)=u(n)-H(S_apr (n))，y(n)有两部分组成，一是测量噪声v(n)，定义测量误差v(n)的协方差矩阵为R(n)=E[v(n)*v(n)^T]，R(n)矩阵大小为3*3。二是J_H (S_apr (n) )[S(n)-S_apr (n) ]这是因为模型过于理想而导致的信息缺失。因此我们可以求得y(n)的协方差矩阵为

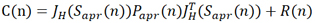    (13)

其中和R(n)在统计特性上相互独立，因此可以定义卡尔曼增益为

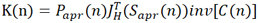    (14)

矩阵运算会让卡尔曼增益的理解变得困难，如果是标量运算，卡尔曼增益将变得简单，C(n)可以理解为缺失信息和测量误差总和，K(n)就是缺失信息占C(n)的比例。获得卡尔曼增益后更新状态向量S(n)：

S(n)=S_apr (n)+K(n)y(n)   (15)

K(n)y(n)是根据卡尔曼增益，从y(n)中得到的缺失信息，由于y(n)中既混合测量噪声又包括缺失信息，因此并不能从K(n)y(n)中获得缺失信息并屏蔽测量噪声，实际上缺失信息和测量噪声按照同样的比例关系（卡尔曼增益）被更新到状态向量S(n)中。所以S(n)中混合了部分测量噪声而且仍然是信息缺失的，缺失的信息更新如下：

P(n)=P_apr (n)-K(n)J_H (S_apr (n))P_apr (n)   (16)

K(n)J_H (S_apr (n))P_apr (n)代表S(n)中已经通过K(n)y(n)获得信息，那么P(n)就代表状态向量S(n)中残留缺失信息，用于下一次迭代。也可以认为我们通过卡尔曼滤波器从新获得了部分缺失信息K(n)J_H (S_apr (n))P_apr (n)，更新后的P(n)代表S(n)尚缺少的信息，将被用于S(n+1)次的状态迭代。

2、实践中的修正

在图2中，虚线圆是我们要跟踪的圆形待测目标，实心小圆点是待测目标上的雷达反射点，实心方形小点是实心圆的平均值，在图2中圆形待测目标按照虚直线运动，而由于我们待测目标上测量点的漂移，实际得到的待测目标的运行轨迹是实折线。因此公式y(n)=u(n)-H(S_apr (n))将不仅仅包含测量噪声，在实际测量中还需要考虑测量点漂移带来的噪声。解决办法是将测量点聚类后，动态估计待测目标的大小，因为测量点只能在待测目标上漂移，可以将待测目标大小乘以0.25作为测量点漂移误差。

图2、测量点漂移示意图

3、雷达简介

首先采用NXP公司的TEF8102和S32R274实现了一款77GHz毫米波长距雷达，采用FMCW调制方式，具体设计参数配置如表1所示，一次测量序列由128个啁啾组成，每个啁啾内采样512点，啁啾内模数转换器采样速率为20MSPS，一个啁啾持续时间为45us，128个啁啾组成一个序列完成一次测量，128个啁啾持续时间为45us*128=5.76毫秒，加上额外的处理时间，本雷达设计完成一次距离，速度和角度的测量周期为30ms。也即每30ms雷达会上报一次待测目标的距离，速度和角度信息，由于一次测量周期30ms相对较短，我们假设在30ms之内，待测目标按照匀加速度进行运动。

表1、77GHz毫米波长距雷达参数配置表

参数	数值
载波频率（Hz）	7.70E+10
载波波长（米）	3.90E-03
采样间隔（秒）	5.00E-08
啁啾周期（秒）	4.50E-05
啁啾采样周期（秒）	2.56E-05
单啁啾采样点数	512
啁啾个数	128
扫频带宽（Hz）	2.00E+08
距离分辨率（米）	7.50E-01
速度分辨率（米/秒）	3.38E-01
无模糊最大速度（米/秒）	2.16E+01
固定单元格最大速度（米/秒）	6.51E+01
无模糊最大距离（米）	1.92E+02

4、仿真验证

为了验证算法的效果，需要将算法输出结果和基准事实进行对比，在实际测试中只能获得实测结果而无法获得基准数据，因此算法的验证通过生成仿真数据的方法。假设待测目标长10米，宽4米，高2米的矩形，按照距离，角度和速度生成1000点测试点，测试点均匀分布于待测目标内，在距离，角度和速度上加高斯白噪，从1000点钟随机挑选10个测试点作为模型的输入数据，待测目标按照匀加速运动。图3横轴代表测量序列，每30ms生成一次仿真数据输入模型，纵轴代表相对误差，单位是百分比，为了直观显示数据，对纵轴数据进行放大，纵轴数据2.5对应误差为100%。由图可知真实测量误差（矩形测量点）远远高于卡尔曼滤波后的误差（图中圆形测量点），显示模型能够有效的对待测目标进行跟踪测量，显示出卡尔曼滤波器在毫米波雷达测量中发挥了重要作用。

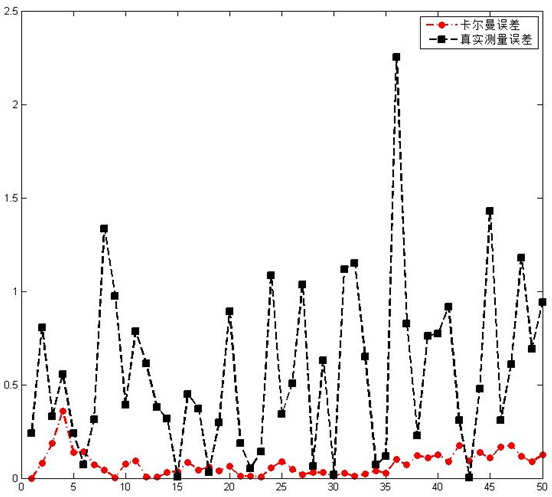
图3、卡尔曼滤波效果对比

5、结论

本文详细介绍了卡尔曼滤波器在毫米波雷达测量领域中的应用，分析了毫米波雷达测量中的误差来源，最后通过matlab仿真验证，结果也证明卡尔曼滤波器可大幅降低毫米波雷达的测量误差。

6、参考

黄小平王岩, 卡尔曼滤波原理及应用, pp. 85, 电子工业出版社

作者：王洪胜、王尧青、张秋英
安富利电子元件（北京射频与微波实验室）

本文MWRF.NET独家版权所有，未经允许不得转载！